
- •1 Статистические методы и модели
- •1.1 Математическое описание динамических систем
- •1.2.4. Приближенное описание случайных процессов
- •2 Статистическая обработка информации
- •2.1 Задачи статистической обработки информации
- •2.4 Математическое описание составляющих объекта
- •Список использованных источников
X 1 |
X |
2 |
|
F1(X1,t1,X2,t2)= ∫ |
∫ |
f(u1,t1, u2,t2)du1du2 |
(1.68) |
−∞ − ∞ |
|
||
откуда следует, что |
|
|
|
f(X1,t1, X2,t2)= ∂2F ( X 1 , t 1 , X 2 , t 2 ) |
(1.69) |
||
|
|
∂x 1∂x 2 |
|
где функция, приведенная в выражении, есть N - мерная функция распределения.
1.2.4. Приближенное описание случайных процессов
Как уже говорилось выше, для полного описания случайного процесса требуется полный набор его реализаций и математическое (в смысле определения вероятностных законов распределения возможных значений процесса) описание его свойств.
Для решения такой задачи в теории стохастических сигналов используется уже известный приём применения характеристик, которые на практике называют моментными или, попросту, начальными или центральными моментами сигнала {X(t)} или совокупности сигналов {X(t)} и {Y(t)}.
Начальным моментом порядка К случайного процесса {X(t)} называется такая функция времени, которая в каждый момент времени t , равна математическому ожиданию К-й степени самого сигнала:
∞
dk(t)=M[Xk(t)]= ∫ Xk(t)f(X,t)dx (1.70)
− ∞
Для определения любого момента dk достаточно знать одномерную функцию плотности распределения вероятностей:
∞ |
(1.71) |
d1(t)=M[X(t)]= ∫ X(t)f(X,t)dx |
|
− ∞ |
|
Это и есть математическое ожидание (или среднее значение) процесса.
Как уже говорилось выше, практически любой (и особенно стационарный по математическому ожиданию ) процесс можно представить себе как аддитивную смесь постоянной (или медленно изменяющейся по среднему значению) мультипликативной составляющей.
ο
Моменты, определяемые для центрированного сигналаX(t) , имеют название центральных:
Центральный момент s-го порядка - это такая функция
времени, которая в каждый момент времени равна математическому ожиданию s -й степени соответствующего
центрированного сигнала.
|
Ο |
∞ |
Ο |
|
(1.72) |
µ s( t ) = M [ |
X |
s ( t )] = ∫ |
X |
s ( t ) f ( x, t )dx |
|
|
− ∞ |
|
|
Моменты 0-го и 1-го порядка неинформативны, так как
µ0 ( t ) = 1; µ1(t ) = 0
Основное применение получил второй центральный момент:
Ο |
|
µ s ( t ) = M [ X 2 ( t )] = D x ( t ) |
(1.73) |
Это - дисперсия сигнала, которая характеризует степень разбросанности отдельных реализаций относительно математического ожидания.
Ту же информацию о процессе {X(t)} дает и среднее квадратическое отклонение, численно равное квадратному корню из дисперсии и имеющее размерность самого сигнала.
Для описания случайных процессов используют также смешанные моменты.
Смешанным начальным моментом порядка (k+s) случайного сигнала {X(t)} называется такая функция двух временных аргументов t1 и t2, которая при фиксированных значениях этих аргументов численно равна математическому ожиданию произведения k-й и s-й степеней соответствующих сечений сигнала:
dk,s(t1,t2)=M[Xk(t1)Xs(t2)] |
(1.74) |
Центральный смешанный момент порядка (к+s) определяется выражением вида :
Ο |
Ο |
45 |
|
||
µk, s(t1, t 2 ) = M [X k (t1) X s (t 2 )] |
(1.75) |
|
Для приближенного описания свойств случайного процесса наиболее широкое применение получил центральный смешанный момент порядка (1+1):
ο |
ο |
|
µ1,1(t1, t 2 ) = M [X(t1) X(t2 )] = R x (t1, t2 ). |
(1.76) |
|
- математическое ожидание произведения двух сечений центрированного сигнала. Это - уже упоминавшаяся автокорреляционная функция случайного сигнала {X(t)} (авто- т. е. характеризуется корреляция, или взаимосвязь двух сечений одного и того же процесса).
Таким образом, для приближенного описания свойств сигнала используют математическое ожидание, дисперсию и автокорреляционную функцию.
Выясним, о каких свойствах сигнала несет информацию АКФ,
адля этого рассмотрим ее собственные свойства.
1)АКФ обладает свойством симметричности относительно своих аргументов, то есть не изменяет своего значения при перемене временных аргументов местами:
Rx(t1,t2)= Rx(t2,t1) |
(1.77) |
2) По величине АКФ не может превышать произведения среднеквадратических отклонений соответствующих сечений:
Rx(t1,t2x)<= σx(t1) σx(t2) |
(1.78) |
3)При совпадении временных аргументов АКФ превращается
вдисперсию:
0 |
(1.79) |
R x ( t , t ) = M [ X 2 ( t )] = D x ( t ) . |
То есть набор характеристик, необходимых для приближенного описания случайного сигнала, может быть сокращен
до двух: mx и Rx(τ).
Вернемся ко второму свойству АКФ и положим t1=t2=t:
Rx(t, t)<= σ2x(t), т. е.
Rx(t, t)<=Dx(t). |
(1.80) |
Наибольшее значение АКФ имеет при равных временных аргументах, и это наибольшее значение равно дисперсии сигнала. На практике для удобства часто используют нормированную автокорреляционную функцию, под которой понимают функцию вида
|
|
|
|
|
|
|
|
|
Ο Ο |
|
|
ρ |
x |
(t |
1 |
, t |
2 |
) = |
R x ( t1, t2 ) |
= |
M [ X ( t1) X ( t2 )] |
(1.81) |
|
σx ( t1)σx ( t2 ) |
|||||||||||
|
|
|
|
|
σx ( t1)σx ( t2 ) |
|

Нормированная АКФ - величина безразмерная. По определению нормированная АКФ - это коэффициент корреляции между двумя сечениями случайного процесса.
Рассмотрим, как будут трансформироваться свойства АКФ при переходе к нормированной функции :
1)ρx(t1,t2)= ρx(t2,t1) ;
2)ρx(t1,t2)<=1;
3)при равенстве временных аргументов:
t1=t2=t, ρx(t,t) = 1.
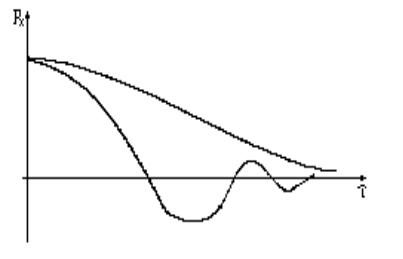
Выясним, как будет вести себя ρx(t1,t2) при изменении
интервала времени между сечениями t1-t2= τ от нуля до бесконечности
Рисунок 17 - Реализация случайного процесса (к вопросу о поведении нормированной АКФ в зависимости от интервала времени между сечениями)
Таким образом, выясняется четвертое свойство АКФ:
lim |
ρ |
x |
(t , t |
|
) = 0 |
(1.82) |
||
t 2 −t1 |
|
→∞ |
|
1 |
2 |
|
|
|
|
|
|
|
|||||
47
Если рассматривать АКФ как функцию интервала времени между сечениями, то это функция при τ, стремящемся к бесконечности, будет стремится к нулю :
4) |
lim ρx (τ) = 0 |
(1.83) |
|
τ→∞ |
|
то есть взаимосвязь между сечениями будет ослабевать и даже теряться (в соответствии с рисунком 17)
Математическое описание системы двух случайных сигналов
Пусть имеем два случайных сигнала {X(t)} и {Y(t)}, каждый из них можно представить в виде совокупности их сечений. Для точного их описания их следует представлять бесконечным числом сечений. То есть, сигналы представляются бесконечным числом случайных величин.
Рисунок 18 - Возможные изменения нормированной АКФ в зависимости от интервала времени между реализациями
Если совместная плотность распределения всех сечений этих сигналов не изменяется при прибавлении ко всем временным аргументам одной и той же величины, то эти сигналы называются
стационарными и стационарно - связанными.
Рассмотрим приближенное описание свойств системы двух сигналов. Для этого будем использовать моментные характеристики.
Для каждого из сигналов указывают его математическое ожидание и АКФ :
mx(t), my(t); Rx(t1,t2), Ry(t1,t2).
Кроме этих характеристик вводится еще одна: взаимная корреляционная функция Rxy(t1,t2) (ВКФ).
Взаимной корреляционной функцией между двумя сигналами {X(t)} и {E(t)} называется такая функция времени, которая при фиксированных значениях временных аргументов равна математическому ожиданию произведения соответствующих сечений этих сигналов:
ο |
ο |
|
R yx (t1, t 2 ) = M [ Y(t1) X(t 2 )]. |
(1.84) |
|
Иногда вместо этой функции используют нормированную ВКФ :
|
|
R yx (t1, t 2 ) |
|
ο |
ο |
|
|
||
ρyx (t1, t 2 ) |
= |
= |
M [ Y(t1) X(t 2 )] |
|
(1.85) |
||||
σy (t1)σx (t |
2 ) |
σy (t1)σx (t 2 ) |
|
||||||
|
|
|
|
|
|||||
Как видно из формулы (1.85) , ρyx - это коэффициент |
|||||||||
корреляции между сечениями Y(t1) и X(t2). |
|
|
|
||||||
Рассмотрим свойства этих функций: |
|
|
|
||||||
1) Ryx(t1,t2)=Rxy(t2,t1), так как |
|
|
|
|
|
||||
Ο |
|
Ο |
|
|
Ο |
Ο |
|
|
|
R yx (t1, t 2) = M[Y(t1) X(t 2)] = M[X(t 2) Y(t1)] = R xy (t 2, t1) |
(1.86) |
||||||||
Взаимная |
корреляционная |
функция |
несимметрична |
||||||
относительно своих аргументов. |
|
|
|
|
|
|
|||
ρyx(t1,t2)= ρxy(t2,t1); |
|
|
|
|
|
|
|
||
2) Ryx(t1,t2)<= |
σy(t1) σx(t2); |
|
|
|
|
|
|||
ρyx(t1,t2)<=1 |
|
|
|
|
|
|
|
(1.87) |
|
3) при одинаковых значениях временных аргументов: |
|
||||||||
|
|
Ο |
Ο |
|
|
|
- |
|
(1.88) |
R yx (t , t ) = M [ Y (t ) X (t )] = D yx (t ). |
|
||||||||
взаимная дисперсия.
Ryx(t1,t2) описывает степень линейной статистической взаимосвязи между временными сечениями различных сигналов. Пусть t2-t1= τ - интервал времени между сечениями.
49
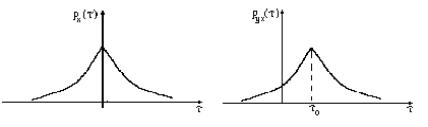
Рисунок 19 - Графики зависимостей АКФ и ВКФ от интервала времени между сечениями
АКФ симметрична, и для ее описания можно изучать только одну ветвь, а в случае ВКФ необходимо исследовать обе ветви.
Нормированная ВКФ достигает своего максимума при τ0, то
есть два сигнала наиболее линейно связаны при этом сдвиге между их временными сечениями.
Если ρyx( τ)=1, то сигналы X(t) и Y(t) |
связаны |
линейной |
функциональной зависимостью при τ= τ0. Все |
понятия |
можно |
обобщить на случай системы произвольного числа сигналов {X (t)},
→
i=1, N .
Для этого достаточно установить mxi(t) - математические ожидания всех сигналов;
Rxi(t1,t2) - АКФ всех сигналов;
Ryi,xj(t1,t2) - ВКФ между всеми парами сигналов.
Математическое описание стационарных случайных сигналов
Пусть имеем случайный процесс X(t), который является стационарным. При этом его одномерная плотность вероятности будет зависеть только от X и не будет зависеть от времени:
f(X,t)=f(X) |
(1.89) |
Не будут зависеть от времени и все начальные и центральные |
|
моменты : |
|
dk(t)=dk |
|
µ k(t)= µk |
|
и, в частности, дисперсия |
|
Dx(t)= σ2x=Dx. |
|
Для АКФ справедливо следующее соотношение: |
|
Rx(t1,t2)=Rx(t2-t1), то есть АКФ зависит не от начала отсчета, а лишь от сдвига между временными сечениями.
Дисперсия характеризует мощность стационарного случайного сигнала, например:
i(t)=X(t), P(t)=i2(t)*R, M[P(t)]=R*M[X2(t)].
То есть, если предположить, что сигнал центрирован, то это выражение представляет его дисперсию (мощность, выделяемую на единичной нагрузке).
Рассмотрим свойства АКФ стационарного случайного сигнала. t2-t1= τ; Rx(t2-t1)=Rx( τ).

1) По величине АКФ процесса не может превышать его
дисперсию;
Rx( τ)<=Dx= σ2x;
2) АКФ - четная функция своего аргумента :
Rx( τ)=Rx(- τ);
3)АКФ при нулевом аргументе равна дисперсии сигнала: Rx(0)=Dx.
Для нормированной корреляционной функции эти свойства трансформируются следующим образом :
1)ρx( τ)<=1;
2)ρx( τ)= ρx(- τ);
3)ρx(0)=1.
Общим для АКФ и нормированной АКФ стационарного случайного сигнала является то, что при неограниченном увеличении временного сдвига между сечениями обе они стремятся к нулю :
lim R x (τ) = lim ρx (τ) = 0
τ→∞ τ→∞
При описании свойств стационарного процесса часто указывают такой интервал времени, начиная с которого можно считать ρx=0. Это - интервал корреляции, который принято
обозначать τk. τk показывает, в каком промежутке времени сечения
сигнала сильно коррелированы (при τ> τk эти сечения считаются некоррелированными ). Кроме того, интервал корреляции несет информацию о частотных свойствах сигнала, определяет длительность АКФ во времени.
Рассмотрим методы определения τk.
1) Выбирается малая величина δ<< 1, и на расстоянии от оси времени проводятся две прямые, параллельные этой оси (в соответствии с рисунком 20).
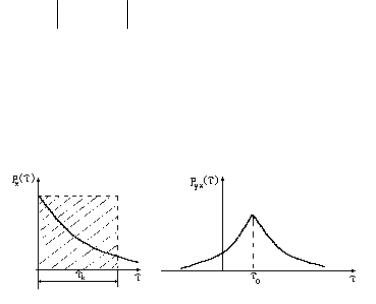
Рисунок 20 - Определение интервала корреляции (метрологический подход)
Тот момент времени, начиная с которого удовлетворяется условие ρ x ( τ) < δ, принимают за τk. Величину δ обычно
принимают равной 2 - 5% от 1.
2) На оси времени как на основании строится прямоугольник, высота которого равна единице, а площадь равна площади всей фигуры под кривой нормированной АКФ (в соответствии с рисунком 21).
Рисунок 21 - Определение интервала корреляции (формантный подход)
∞
τk= ∫ ρ x ( τ) d τ (1.90)
0
Этот метод применяется для определения τk монотонных,
не знакопеременных АКФ.
Для вычисления знакопеременных АКФ принято использовать следующие три подхода:
|
|
∞ |
|
|
|
|
|
|
3) |
τk= ∫ |
|
ρ x ( τ) |
|
d τ |
(1.91) |
||
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∞ |
|
|
|
|
|
|
|
4) |
τk= ∫ ρ2x ( τ)dτ |
(1.92) |
||||||
|
0 |
|
|
|
|
|
|
|
5) |
τk= |
µ N |
|
(1.93) |
||||
µ |
N −1 |
|||||||
|
|
|
|
|||||
где µN - момент АКФ, определяемый соотношением

∞
µN = 0∫ τNρx(τ)dτ
N - любое целое положительное число.
Из приведенных методов наиболее часто на практике используется четвертый.
Посмотрим, какой из приведенных способов дает наибольшее значение интервала корреляции :
∞∞
τk1= 0∫ ρx(τ)dτ<= 0∫ ρx (τ) dτ= τk2
|
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
|
|||
τk3= |
∫ ρ2 |
( |
τ |
|
τ |
∫ |
|
ρ (τ) |
|
ρ (τ) |
|
dτ |
<= |
∫ |
|
ρ τ |
|
τ |
||||||
|
|
|
|
|
|
|||||||||||||||||||
0 |
x |
|
)d = |
0 |
|
|
x |
|
x |
|
|
0 |
|
x( ) |
|
d |
= τk2 |
|||||||
так как |
|
ρ (τ) |
|
<=1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Таким |
|
образомx |
, |
|
|
|
|
|
|
|
|
|||||||||||||
|
τk1<= τk2, τk3<= τk2. |
|
|
|
|
|
|
|||||||||||||||||
Пример.
Пусть имеем стационарный случайный процесс X(t) с нормированной корреляционной функцией
ρx (τ) = e−d τ
53
и определим его интервал корреляции первыми четырьмя способами:
e-d |
|
τ |
|
= δ; -d τ=ln δ; τk= |
1 |
ln 1 |
|
|
|||||
|
|
|
d |
|||
|
|
|
|
|
δ |
То есть, чем больше тем круче спадает АКФ, и тем меньше величина интервала корреляции.
∞ |
|
∞ |
|
|
|
|
|
τk1= ∫ e−dτdτ= |
1 |
; τk2= ∫ e−dτdτ = |
1 |
; |
|||
d |
d |
||||||
0 |
0 |
|
|
|
|||
|
|
|
|
|
|||
∞ |
|
|
|
|
|
|
|
τk3= ∫ e−2dτdτ = |
1 |
. |
|
|
|||
|
|
|
|||||
0 |
|
|
2 d |
|
|
||
|
|
|
|
|
|
||
Приближенное описание АКФ
Во-первых, АКФ может быть приближенно описана интервалом корреляции. Кроме этого, для приближенного описания АКФ используются моментные характеристики этой функции.
Нормированным моментом порядка К АКФ называется величина
∞
µk = ∫ τkρx(τ)dτ |
(1.94) |
0 |
|
Если К = 0, то µk = τk, то есть интервал корреляции
представляет собой момент АКФ нулевого порядка. Для приближенного описания АКФ используют ее модель
ρM (β1, β2,..., βN, τ)
где β 1,..., β N - коэффициенты (параметры ) модели.
Для описания АКФ необходимо отыскать значения этих параметров, что можно проделать, используя метод моментов, согласно которому моменты истинной АКФ должны равняться моментам модели функции корреляции:
µk =µ(kM ) ,k = 1, 2, 3,... |
(1.95) |
Использование метода моментов позволяет достаточно точно
описывать АКФ при больших значениях τ.
При малых τ более целесообразно пользоваться критерием производных, который сводится к тому, что коэффициенты модели
вычисляются приравниванием соответствующих |
производных |
нормированной АКФ и ее модели в нуле: |
|
ρ(xk ) (0) = ρx (0), k =1, 2, 3,... |
(1.96) |
Описание системы стационарных и стационарно связанных сигналов
Пусть имеем два случайных сигнала, которые стационарно связаны между собой.
Взаимная корреляционная функция (ВКФ) системы имеет вид
ο ο
R xy (t1, t 2 ) = M [X(t1) Y(t 2 )]

Для описания системы двух случайных процессов необходимо знать двумерную плотность вероятности
f[X(t1), Y(t2)] = f(X, t1+u;Y, t2 +u) |
(1.97) |
Выражение (1.97) представляет собой условие стационарной связанности.
Как и в случае АКФ, положим τ=t2-t1. Рассмотрим свойства ВКФ системы двух стационарно связанных сигналов.
1) Так как
Rxy(t1,t2)=Ryx(t2,t1),
то Rxy( τ)=Ryx(- τ) (1.98) (в соответствии с рисунком 22)
Рисунок 22 - График ВКФ системы двух стационарно связанных сигналов
2) Аналогично, |
|
( τ)<= σ |
|
σ |
|
|
||
|
R |
x |
y |
(1.99) |
||||
|
xy |
|
|
|
|
|
||
|
Rxy(0) ≠ σxσy |
|
55 |
|||||
3) |
|
(1.100) |
||||||
Нормированная функция взаимной корреляции |
|
|||||||
|
ρxy (τ) = |
R xy (τ) |
|
|
(1.101) |
|||
|
σx σy |
|
||||||
|
|
|
|
|
||||
обладает аналогичными свойствами:
1)ρxy (τ) = ρyx (−τ);
2)ρxy (τ) ≤1.
Для приближенного описания ВКФ используется ряд характеристик: координата и величина экстремума, интервал
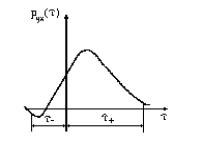
взаимной корреляции, моментные характеристики и производные ВКФ при различных значениях аргумента.
Интервал взаимной корреляции двух стационарно связанных случайных сигналов определяется как интервал времени, внутри которого ВКФ отлична от нуля, а вне его -равна или близка к нулю (в соответствии с рисунком 23).
Рисунок 23 - К вопросу об определении интервала взаимной корреляции
Способы отыскания сходны со способами определения интервала корреляции с отличием, что в данном случае приходится оценивать взаимодействие как в положительной, так и в отрицательной области.
1)ρxy (τ) = δ
∞ |
0 |
∞ |
2)τкв= −∞∫ ρxy(τ)dτ= −∞∫ ρxy(τ)dτ+ 0∫ ρxy(τ)dτ=
∞∞
= 0∫ ρyx(τ)dτ+ 0∫ ρxy(τ)dτ
|
|
|
∞ |
||||
3) |
τкв= |
|
∫ |
|
ρxy(τ) |
|
dτ |
|
|
−∞ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
∞ |
||||
4) |
τкв= |
∫ ρ2xy(τ)dτ |
|||||
|
|
|
−∞ |
||||
(1.102)
(1.103)
(1.104)
(1.105)
Так же, как и в случае АКФ для приближенного описания ВКФ используют ее моменты, которые определяются следующим образом
∞
µ(xyq) = ∫ τqρxy (τ)dτ (1.106)
0
q - порядок момента.
Если известна координата максимального значения ВКФ, то можно использовать и такие моменты :
∞ |
|
εq = ∫(τ − τ0)q ρxy (τ)dτ |
(1.107) |
0 |
|
1.2.6 Обобщенные модели случайных процессов (по Пугачеву)
Всякий случайный процесс может быть представлен в виде
Ο |
|
X(t) = mx(t)+ X (t) |
(1.108) |
и описан моделью |
|
∞ |
|
X(t) = mx(t)+ ∑ U k ϕk (t ) , |
(1.109) |
k =1
где: Uk - коэффициенты разложения случайной величины;
57
ϕk (t) - координатные, детерминированные функции.
Вкачестве критерия адекватности модели исследуемому сигналу можно взять критерий минимума среднеквадратической погрешности
∆ =M[{ Xм(t)-X(t)}2] = min |
(1.110) |
∞ |
|
M[Xм(t)] = M[mx(t)]+ ∑ M [U k ]ϕk (t ) |
(1.111) |
k =1
Чтобы обеспечить равенство математических ожиданий модели и сигнала необходимо, чтобы сумма равнялась нулю. Это возможно, когда все случайные величины Uk центрированы. Дальнейшее построение модели сводится к отысканию Uk.
∆ =min
Ο |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ U k ϕk (t ) |
|
|
|
|
|
|
(1.112) |
|||||
X M (t)= |
|
|
|
|
|
|
||||||||
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
∆ =M[{ |
Ο |
Ο |
|
|
|
|
|
|
|
|
|
(1.113) |
||
X M (t)- X (t)}2]=min. |
|
|
|
|
|
|
||||||||
Это выполняется при |
∂ ∆ |
|
|
=0, |
|
|
|
|||||||
∂ ϕ k ( t ) |
|
|
|
|
||||||||||
|
|
|
∂ ∆ |
|
|
|
|
|
|
|
∂ |
Ο |
|
|
или |
|
|
|
|
Ο |
|
Ο |
|
X M |
]=0. |
||||
|
|
|
|
=M[{ X M |
(t)- |
X |
(t)} |
|
||||||
|
∂ ϕ k |
( t ) |
|
|||||||||||
|
|
∂ ϕ k ( t ) |
||||||||||||
|
|
|
|
|
|
|
Ο |
|
|
|
|
|
|
|
Но |
|
|
|
|
|
∂ X M |
=Uk, |
|
|
|
|
|||
Ο |
Ο |
|
|
∂ ϕ k ( t ) |
|
|
|
|
||||||
M[{ |
|
]=0, |
|
|
|
|
|
|
|
|||||
X M (t)- X (t)}Uk |
|
|
|
|
|
|
|
|||||||
отсюда |
Ο |
|
Ο |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
M[ X M (t)Uk]=M[ X (t)Uk] |
|
|
|
|
|
|
(1.114) |
|||||||
∞ |
|
|
|
|
|
|
|
|
|
|
Ο |
|
|
|
∑ M [U m U k ]ϕm (t ) |
|
|
|
|
|
|||||||||
= M[ X (t)Uk]k=0,1,... ∞ (1.115) |
||||||||||||||
m =1
Это нереально, поэтому кроме требования центрированности, накладываем еще одно условие
οο
M[ U m (t) U k (t)]=Rm,k.
Для того, чтобы избежать необходимости решать систему уравнений, потребуем выполнения условия ортогональности
D k , m = k |
(1.116) |
Rm,k= |
|
0, m ≠ k |
|
то есть случайные величины U должны быть некоррелированными.
M |
ο 2 |
=Dk |
|
U k |
|
||
Ο |
|
|
|
Dk ϕk (t) =M[Uk X (t)], k=1,2,3,... |
(1.117) |
||
Вместо системы уравнений получаем совокупность уравнений, каждое из которых имеет единственное неизвестное.
Определяем координатные функции
|
Ο |
|
M |
[ U k X ( t ) ] |
|
ϕk (t) = |
D k |
(1.118) |
при известной дисперсии.
Или наоборот, задаваясь координатными функциями, отыскиваем дисперсии
|
|
|
Ο |
|
|
Dk= |
M [ U |
k |
X ( t ) ] |
(1.119) |
|
ϕ k |
( t ) |
||||
|
|
||||
Вывод: любой случайный процесс X(t) можно описать моделью
∞
XМ(t) = mx(t)+ ∑ U k ϕk (t )
k =1
причем математические ожидания модели и сигнала должны совпадать, а коэффициенты разложения представляют центрированные и некоррелированные случайные величины.
Ο
Dk ϕk (t) =M[Uk X (t)].
Ο
Так как Dk ϕk (t) ≠0, то и M[Uk X (t)] ≠0, следовательно,
любой коэффициент разложения должен быть коррелирован с самим сигналом X(t).
Вычислим минимальное значение среднеквадратической погрешности.
Итак, центрированная модель имеет вид
Ο |
∞ |
|
|
X (t)= ∑ U k ϕk (t ) . |
|
|
k =1 |
Среднеквадратическая погрешность определяется выражением
Ο |
|
Ο |
|
∆ =M[{ X M (t)- X (t)}2]. |
|
||
Или |
|
|
|
Ο 2 |
Ο |
Ο |
Ο |
∆ =M[ X М (t)]-2M[ X M (t) X (t)]+M[ X 2(t)]
причем последнее слагаемое равно дисперсии исследуемого сигнала.
Ο 2 |
|
|
|
N |
N |
|
|
|
|
|
|
|
|
N |
|
X М (t)= ∑ |
∑ ϕk |
(t)ϕm (t)M[U k U m ] = ∑ D k ϕ2k (t) , |
|||||||||||||
|
|
|
|
|
k =1 m =1 |
|
|
|
|
|
|
|
|
k =1 |
|
Ο |
|
|
|
|
Ο |
∞ |
|
|
|
|
|
Ο |
|
|
|
|
|
|
|
∑ U k ϕ k ( t ) X ( t ) , |
|
|
|||||||||
X M (t) X (t)= |
|
|
|||||||||||||
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
Ο |
|
|
Ο |
|
∞ |
|
|
|
|
Ο |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M[ X M (t) X (t)]= ∑ϕk (t)M[U k X(t)] , |
|||||||||||||||
но |
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ο |
|
|
|
|
ϕ2 (t) , то есть |
|
|
|
||||
M[U X (t)]= |
∑ D |
k |
|
|
|
||||||||||
|
|
k |
|
|
|
k =1 |
|
|
k |
|
|
|
|
||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
||
|
Ο |
|
|
Ο |
|
|
|
|
|
|
|
|
|||
M[ X M |
|
(t) X (t)]= ∑ D k ϕ2k (t) , |
|
|
|
||||||||||
|
|
|
|
|
|
N |
k =1 |
|
N |
|
|
|
|||
∆ |
|
|
|
|
|
|
|
|
|
ϕ2 |
|
ϕ2 |
(t) , |
||
min |
=D (t)-2 ∑ D |
k |
(t) + ∑ D |
k |
|||||||||||
|
|
|
x |
k =1 |
|
|
k |
k =1 |
k |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆ |
|
|
|
|
N |
|
|
|
|
ϕ2 |
(t) |
|
|
|
|
min |
=D (t)- ∑ D |
k |
|
|
(1.120) |
||||||||||
|
|
|
x |
k =1 |
|
|
k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда видно, что среднеквадратическая погрешность
60
убывает до нуля, когда N стремится к бесконечности.
N
Выражение ∑ D k ϕ2k (t) , будем считать дисперсией модели.
k =1
Минимальную среднеквадратическую погрешность чисто формально можно представить в виде
∆ |
|
|
|
N |
|
|
|
(t)ϕ |
|
(t |
|
) }| t=t , |
|
min |
={R (t, t |
)- |
∑ D |
k |
ϕ |
k |
k |
1 |
(1.121) |
||||
|
x 1 |
|
k =1 |
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где: Rx(t,t1)-АКФ сигнала. Отсюда можно предположить, что
N
∑ D k ϕk (t)ϕk (t1) = RМ(t, t1) - АКФ модели.
k =1
Обратимся к модели и найдем ее функцию корреляции:
|
Ο |
Ο |
N |
N |
|
RМ(t,t1)=M[ X M (t) X |
(t1)]=M[ ∑ |
∑ ϕk (t)ϕm (t1)U kU m = |
|
||
|
|
|
k =1 m =1 |
|
|
N |
N |
|
|
N |
|
= ∑ |
∑ ϕk (t)ϕm (t1)M[U kU m ] = ∑ D k ϕk (t)ϕk (t1) |
(1.122) |
|||
k =1 m =1 |
|
|
k =1 |
|
|
то есть наше предположение о виде АКФ модели верно.
Таким образом, минимум среднеквадратической погрешности определяется выражением
∆ min={Rx(t, t1)- RМ(t,t1)}| t=t |
(1.123) |
1 |
|
Выводы :
1.В качестве модели АКФ случайного процесса можно брать
ееканоническую модель :
|
|
|
N |
|
|
|
(t)ϕ |
|
(t |
|
) , |
R |
(t, t |
)= |
∑ D |
k |
ϕ |
k |
k |
1 |
|||
М |
1 |
|
k =1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
и чем точнее модель АКФ, тем точнее будет модель самого сигнала. 2. Из выражения для канонической модели АКФ вытекает каноническая модель сигнала, и для построения последней
необходимо предварительно синтезировать каноническую модель
его функции корреляции.
1.2.6 Математическое описание стационарных случайных сигналов в частотной области
Настоящий раздел посвящен рассмотрению частотных, или спектральных свойств стационарных случайных процессов. В зависимости от того, на ограниченном или неограниченном промежутке времени исследуется сигнал, эти свойства разительно отличаются друг от друга.
Спектральное представление стационарного случайного
сигнала, рассматриваемого на ограниченном интервале времени
Ο
Пусть X (t) - центрированный стационарный случайный процесс на участке 0<=t<=T, а Rx(t,t1) - АКФ этого процесса.
Ο
Так как X (t) - стационарный сигнал, то его корреляционная функция является функцией одного аргумента:
Rx(t,t1)=Rx(t1-t)=Rx( τ),
где τ=t1-t. Найдем диапазон изменения τ :

0 |
≤ t |
≤ T -T<=t1-t<=T; -T<= τ<=T. |
0 |
≤ t1 ≤ T |
|
На рисунке 24 изображен график зависимости АКФ от интервала между сечениями.
Рисунок 24 - График АКФ ограниченного во времени стационарного случайного процесса
Построим каноническую модель АКФ, для этого представим ее в виде тригонометрического ряда Фурье :
|
b 0 |
∞ |
∞ |
|
|
Rx(τ)= |
+ ∑ bkcos(kw τ)+ ∑ λksin(kw τ). |
(1.124) |
|||
|
|||||
2 |
k =1 |
k =1 |
|
||
|
|
|
|||
62
Определим коэффициенты ряда :
|
|
T0 |
2 |
|
|
|
|
T0 |
2 |
|||
|
|
|
|
|
Rx( τ)cos(kw τ)d τ; λk= |
|
|
|||||
bk= |
2 |
|
∫ |
|
|
|
2 |
∫ Rx(τ)sin(kwτ)dτ. |
||||
|
|
|
|
T |
||||||||
T |
|
|
|
|
||||||||
0 |
− T0 |
2 |
|
0 |
− T0 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
w= |
2π |
|
; |
λ |
|
|
|
||||
|
|
|
|
|
||||||||
|
T0 |
k=0, так как АКФ - четная функция своего аргумента, |
||||||||||
|
|
|
|
|
|
|
|
|
||||
Sin - нечетная, а интеграл от нечетной функции в симметричных пределах равен нулю;
bk=Dk, тогда
|
|
|
|
D 0 |
|
|
∞ |
||||
Rx( τ)= |
+ |
∑ Dkcos(kwτ); |
|||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
T0 |
|
|
|
|
|
|||
Dk= |
2 |
|
|
∫2 |
Rx(τ)cos(kwτ)dτ, избавляемся от T0: |
||||||
T |
|
||||||||||
0 |
−T0 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
w= |
2π |
= |
2π |
= |
π |
, тогда |
|||||
T0 |
2T |
||||||||||
T |
|||||||||||
|
|
|
|
|
|
||||||

|
|
T |
|
Dk= |
1 |
∫ Rx( τ)cos(kw τ)d τ. |
|
T |
|||
|
− T |
||
|
|
Докажем, что эта модель является канонической, для этого вместо подставим его значение
R (t, t ) D 0 ∞ D cos(kw(t t ))
x 1 = 2 + k∑=1 k − 1
но cos(kw(t-t1)=cos(kwt- kwt1)=cos(kwt)cos(kwt1)+ +sin(kwt)sin(kwt1), тогда
Rx(t, t1) = D20 +
Таким образом,
∞
∑ Dk(cos(kwt)cos(kwt1) + sin(kwt)sin(kwt1)).
k=1
сам сигнал может быть представлен в виде :
∞ |
∞ |
|
X(t) = Ф + ∑U k cos(kwt) + ∑Vk sin(kwt) |
(1.125) |
|
k =1 |
k =1 |
|
Коэффициенты разложения при этом обладают следующими свойствами :
1) M[Ф]=M[Uk]=M[Vk]=0,
63
то есть все они центрированы; 2)Коэффициенты разложения некоррелированы между собой :
M[ФUk]=M[ФVk]=0 при любых к.
0, k ≠ m 3) M [U kU m ] = D k , k = m
0, k ≠ m M [Vk Vm ] = D k , k = m
4)M[UkVm]=0
D[Ф] = D20
То есть сигнал описывается разложением :
∞
X(t) = Ф + ∑(U k cos(kwt) + Vk sin(kwt)) =
k =1
∞
= Ф + ∑( A k sin(kwt + ϕk )
k =1
где

A |
|
= |
U |
2 |
+ V |
2 |
; ϕ |
k |
= arctg( |
Vk |
). |
|
k |
k |
k |
|
|||||||||
U k |
||||||||||||
|
|
|
|
|
|
|
Любой стационарный случайный сигнал может быть представлен в виде бесконечного ряда тригонометрических функций со случайными амплитудами и фазами.
Определим дисперсию k-й гармоники:
Dk=M[{Ukcos(kwt)+Vksin(kwt)}]=cos2(kwt)M[Uk2]+
+2sin(kwt)cos(kwt)M[UkVk]+sin2(kwt)M[Vk2]. (1.126)
Дисперсия Dk характеризует мощность k-й гармонической составляющей канонической модели сигнала.
Зависимость величины Dk от частоты получила название спектра случайного сигнала или спектра мощности случайного сигнала или энергетического спектра.
|
|
|
|
1 |
T |
|
|
D k = |
|
∫ R x (τ) cos(kwτ)dτ; |
|
||||
T |
|
||||||
|
|
|
|
−T |
|
||
|
D 0 |
|
|
|
∞ |
|
|
R x (t, t1 ) = |
|
+ ∑ D k cos(kw(t − t1 ) |
(1.127) |
||||
2 |
|||||||
|
|
|
|
|
k =1 |
|
|
64
Рисунок 25 - Энергетический спектр случайного сигнала
Спектр случайного сигнала, ограниченного во времени, имеет линейчатую, дискретный характер, он определен на строго фиксированных частотах.
Спектр обладает следующими основными свойствами: 1)Он неотрицателен
Dk=>0.
2)Представляет собой четную функцию k:

Dk=D-k.
3)Положим τ = 0:
D D 0 ∞ D ,
x = 2 + k∑=1 k
то есть энергия (мощность) всего сигнала складывается из мощности (энергии) постоянной составляющей и всех гармоник.
4)Рассмотрим, как ведет себя дисперсия k-й гармоники при неограниченном увеличении промежутка времени Т.
|
|
|
1 |
T |
|
|
2 |
T |
|
|
2D x |
T |
|
|
2D x τ |
|
|
|
D |
k |
= |
∫ |R |
x |
(τ)|dτ = |
∫|R |
x |
(τ)|dτ < |
∫|ρ |
x |
(τ)|dτ = |
к |
(1.12) |
|||||
T |
T |
|||||||||||||||||
|
|
−T |
|
0 |
|
T |
0 |
|
T |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где τk |
= ∫|ρx (τ)|dτ - интервал корреляции процесса X(t). |
|
|
|||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
То есть, D k < 2DT x τк - при увеличении Т дисперсия гармоники убывает.
65
5)Как видно из неравенства (1.128) предел дисперсии при
неограниченном увеличении Т равен нулю |
|
lim D x = 0. |
(1.129) |
T →∞ |
|
Рассмотрим, к чему стремится дисперсия при неограниченном росте порядкового номера номера гармоники k.
Обозначим: kwτ = χ, χв = kwT = kπ, χm = −kπ ,
τ = kwχ , dτ = kwdχ = kwT dχ.
kπ
D k = k1π −∫kπ R x ( kχπ
) cosχdχ;
при больших k
kπ
D k = k1π −∫kπ cosχdχ;
lim D x = 0.
k→∞

То есть, при больших k энергетический спектр затухает. Рассмотрим вопрос определения полосы частот сигнала.
В основу определения частотного диапазона кладется энергетический подход, то есть под полосой частот подразумевает такая, в которой сосредоточена практически вся энергия (мощность) сигнала, а именно - 95%.
N |
|
|
X м(t) = ∑ |
( A k sin(kwt + ϕk ) |
, |
k =m |
|
|
|
|
|
wн = mw; wв = N w. |
|
|
Таким образом, верхняя и нижняя границы полосы частот при известных m и N легко определяются. Ширина спектра при этом:
∆w=(N-m)w
N
D м = ∑D k - мощность сигнала в полосе частот;
k =m
66
N
D м = ∑D k = 0.95D x
k =m
Отсюда ищутся m и N. Но непосредственно таким подходом воспользоваться нельзя, нужны другие способы. Например, предположим, что потери энергии на частотах от 0 до m-1 и от N+1 до ∞ равны, тогда:
m −1
D20 + ∑D k = 0.025D x , (1.130)
k =1
отсюда определяют m;
∞
∑D k = 0.025D x ,
N =N +1
из этого выражения можно найти N, но вычислять сумму бесконечного ряда неудобно, поэтому часто прибегают к такому подходу:

|
|
N |
∞ |
D x = |
D 0 |
+ ∑D k + |
∑D k , |
2 |
|||
|
|
k =1 |
k =N +1 |
это - мощность всего сигнала ;
∞ |
N |
|
|
∑D k = D x − |
D 0 |
− ∑D k = 0.025D x, |
(1. 131) |
2 |
|||
k =N +1 |
k =1 |
|
|
Этим уравнением для определения N воспользоваться проще, для этой же цели можно применить и такое выражение:
N |
|
0.975D x = D20 + ∑D k , |
(1.132) |
k =1
Спектральное представление стационарного случайного
сигнала, рассматриваемого на неограниченном интервале времени
Пусть имеем стационарный случайный сигнал X(t), рассматриваемый на интервале времени 0<=t< ∞ .
67
Для описания его частотных свойств введем в рассмотрение отношение дисперсии k-й гармоники к ширине полосы частот между двумя близлежащими спектральными линиями.
|
|
∞ |
∞ |
|
|
|
∞ |
|||||||||||||
R x (τ) = |
D 0 |
+ ∑ |
D k |
ejkwτ |
+ ∑ |
D k |
|
e− jkwτ |
= ∑ |
D k |
||||||||||
2 |
2 |
2 |
|
2 |
|
|
||||||||||||||
|
|
k =1 |
k =1 |
|
|
|
k =0 |
|||||||||||||
Заменим во второй сумме k на -k: |
|
0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
R x (τ) = ∑ |
D k |
|
ejkwτ |
+ |
∑ |
D k |
|
|
|||||||
|
|
|
|
2 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
k =0 |
|
|
|
k =−∞ |
|||||||||
но Dk=D-k. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∞ |
0 |
|
|
|
|
|
|
|
∞ |
|||||||||
|
|
∑ |
D k |
ejkwτ + |
∑ |
D k |
e− jkwτ |
= |
∑ |
D k |
|
|||||||||
|
|
2 |
2 |
2 |
||||||||||||||||
|
|
k =0 |
k =−∞ |
|
|
|
k =−∞ |
|||||||||||||
∞
ejkwτ + ∑D2k e− jkwτ k =1
ejkwτ ,
ejkwτ . (1.133)
Так как частота w численно равна расстоянию между спектральными линиями, то можно сделать формальную замену :
|
|
|
|
|
|
|
|
∞ |
|
|
|
||
|
|
|
|
R x (τ) = ∑ |
D k |
ejk∆wτ |
|
|
(1.134) |
||||
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
k =−∞ |
|
|
|
||
В свою очередь |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
T |
|
|
|
||
|
|
|
D k |
= |
1 |
∫R x (τ) cos(k∆wτ)dτ |
|
|
(1.135) |
||||
|
|
|
T |
|
|
||||||||
|
|
|
|
|
|
|
|
−T |
|
|
|
||
Найдем отношение |
|
|
|
||||||||||
|
D |
k |
|
1 |
T |
|
|
|
|
* |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
||
|
|
|
= |
|
|
R x (τ) cos(k∆wτ)dτ = S |
(k∆w) |
(1.136) |
|||||
|
∆w |
|
π |
||||||||||
−T
Это - функция k ∆w, обладающая свойствами:
S* (−k∆w) = S* (k∆w) ,
68
то есть S* (k∆w) - четная функция своего аргумента; кроме того она
неотрицательна: S* (k∆w) >= 0.
Перейдем от Dk к введенной нами функции:
|
D k |
= ∆wS* (k∆w) |
|
|
|
|
T |
|
|
S* (k∆w) = |
1 |
∫R x (τ) cos(k∆wτ)dτ |
(1.137) |
|
π |
||||
|
|
−T |
|
|
|
|
|
∞ |
|
R x ( τ) = |
12 ∑ S* e jk ∆w τ ∆w |
(1.138) |
||
k = −∞
Устремим ∆w к нулю, а интервал времени Т к бесконечности. S* (k∆w) при неограниченном увеличении времени наблюдения называется спектральной плотностью.

|
|
|
∞ |
|
R x (τ) = 12 |
∫S* (u) exp( juτ)du |
|
||
|
|
|
−∞ |
(1.139) |
|
|
|
∞ |
|
|
1 |
|
|
|
|
|
|
||
S* (u) = |
|
∫ R x (τ) cos(uτ)dτ |
|
|
π |
|
|||
|
|
|
−∞ |
|
Вместо аргумента u введем w:
|
|
∞ |
|
|
|
R x (τ) = 12 |
∫S* ( w) exp( jwτ)dw |
||||
|
|
−∞ |
|
(1.140) |
|
|
|
∞ |
|
|
|
|
π |
∫ |
|
|
|
S* ( w) = |
1 |
|
R |
x |
(τ) cos( wτ)dτ |
|
|
||||
|
|
|
|
|
|
|
|
−∞ |
|
|
|
Спектральная плотность мощности (СПМ) случайного сигнала обладает теми же свойствами: она является неотрицательной и четной функцией частоты.
Для того, чтобы АКФ можно было представить в виде Фурье - преобразования от СПМ, переобозначим ее:
S(w) = S* (w) 2
В формулах произойдут следующие изменения :
∞
R x (τ) = ∫S( w) exp( jwτ)dw
−∞
∞
S( w) = 21π ∫R x (τ) cos( wτ)dτ
−∞
Рассмотрим свойства новой спектральной плотности:
cos(wτ) = |
ejwτ |
+ e− jwτ |
|
|
2 |
|
|
|
|
|
|
∞ |
|
∞ |
|
∫R x (τ) cos(wτ)dτ = 12 |
∫R x (τ) exp( jwτ)dτ + |
||
−∞ |
|
−∞ |
|
(1.141)
69
(1.142)

∞
+12 ∫R x (τ) exp(−jwτ)dτ
−∞
Впервом интеграле сделаем замену аргумента на противоположный по знаку и т. к. R x (τ) = R x (−τ) , то
∞ |
∞ |
∫R x (τ) cos( wτ)dτ = 12 |
∫R x (τ) exp(−jwτ)dτ + |
−∞ |
−∞ |
∞ |
∞ |
+ 12 ∫R x (τ) exp(−jwτ)dτ = |
∫R x (τ) exp(−jwτ)dτ |
−∞ |
−∞ |
то есть спектральная плотность может быть записана в виде:
∞ |
|
S( w) = 21π ∫R x (τ) exp(−jwτ)dτ |
(1.143) |
−∞
Вывод : АКФ и СПМ связаны между собой парой преобразований Фурье.
Сделаем подстановку: exp(jw τ)=cos(w τ)+jsin(w τ), тогда
∞ ∞
R x (τ) = ∫S( w) cos( wτ)dw + j ∫S( w) sin( wτ)dw ,
−∞ −∞
70
но так как АКФ является четной функцией, а синус — нечетной, то второй интеграл равен нулю, и тогда
|
|
|
|
|
∞ |
|
|
R x (τ) = |
∫S( w) cos( wτ)dw , |
||||
то есть: |
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
R x (τ) = 2 ∫S( w) cos( wτ)dw |
||||||
|
|
|
−∞ |
|
(1.144) |
|
|
|
|
∞ |
|
|
|
|
|
π |
∫ |
|
|
|
S( w) = |
1 |
|
R |
x |
(τ) cos( wτ)dτ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
Укажем некоторые свойства спектральной плотности мощности.
Во-первых, СПМ является четной функцией своего аргумента
S(w) =S(-w),
во-вторых, спектральная плотность - неотрицательная функция:
S(w)>=0,
и в третьих, вычислим дисперсию сигнала:
∞ |
|
D x = R x (0) = ∫S( w)dw . |
(1.145) |
−∞
То есть, интеграл от спектральной плотности в бесконечных пределах равен дисперсии (полной мощности) сигнала. Это - условие нормировки.
Частотный диапазон сигнала и способы его определения
Под частотным диапазоном случайного сигнала понимают такую полосу частот, в которой сосредоточена практически вся его мощность (95%).
Мощность сигнала - это его дисперсия, значит в частотном диапазоне содержится 95% дисперсии. Будем рассматривать только одну ветвь (в соответствии с рисунком 26)
71
Рисунок 26-К вопросу об определении частотного диапазона сигнала
Случайный сигнал будет содержать энергию, соответствующую площади заштрихованной фигуры.

wв |
|
∫S( w)dw = 0.95 D2x |
(1.146) |
wн
Однако это уравнение нельзя использовать для вычисления ширины спектра, так как в него входит два неизвестных.
Существует несколько способов определения частотного диапазона. Рассмотрим первый из них. Предположим, что потери энергии слева и справа от частотного диапазона одинаковы:
wн |
|
||||
∫S( w)dw = 0.025 |
D x |
|
|||
2 |
|
|
|||
0 |
|
|
|
(1.147) |
|
∞ |
|||||
|
|||||
∫S( w)dw = 0.025 |
D x |
|
|
||
2 |
|
||||
wв |
|
||||
S(w) - монотонная функция, т. е. решение единственно. Ширина частотного диапазона по его верхней и нижней границам :
∆wс = wв − wн.
Та частота, на которой спектральная плотность имеет максимум, называется основной частотой сигнала w0.
Если известна основная частота w0, то делается предположение о том, что спектр сигнала симметричен
72
относительно этой частоты:
wв = w0 + ∆wс |
2 |
(1.148) |
|
|
− ∆wс |
2 |
|
wн = w0 |
|
||
Тогда уравнение (1. 146) примет вид
w0 |
+∆w с 2 |
|
|
|
∫S( w)dw = 0.95 |
D x |
(1.149) |
|
2 |
||
w0 −∆w с 2
Вэтом уравнении имеется единственное неизвестное - эквивалентная ширина спектра мощности, и так как СПМ - монотонная функция, то уравнение имеет только одно решение.
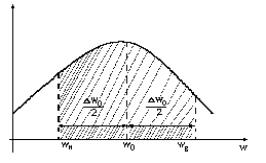
Итак, для определения частотного диапазона необходимо:
1)определить основную частоту w0;
2)решить уравнение и найти эквивалентную ширину спектра мощности;
3)найти верхнюю и нижнюю границы частотного
диапазона.
Возможен и частный случай, когда нижняя граничная частота равна нулю, и приходится определять только верхнюю частоту диапазона:
wв |
|
|
∫S( w)dw = 0.95 |
D x |
(1.150) |
2 |
||
0 |
|
|
Здесь единственное неизвестное - верхняя граничная частота, которая численно равна эквивалентной ширине частотного диапазона ∆wс = wв .
Наибольшее применение на практике получил формантный подход к определению частотного диапазона.
Согласно этому подходу, вначале определяется ширина частотного диапазона. Под ней понимается величина основания прямоугольника (в соответствии с рисунком 27), построенного на оси частот и имеющего высоту, равную максимальному значению СПМ, а площадь - равную площади фигуры, ограниченной кривой спектральной плотности.
73
Рисунок 27 - Формантный метод определения частотного диапазона

∆wсSм = D x 2 |
|
|
||
∆wс = D x 2Sн |
|
(1.151) |
||
wн |
= w0 − ∆wс |
2 |
||
|
||||
wв |
= w0 + ∆wс |
2 |
|
|
Достоинством этого подхода является минимум вычислений. На практике часто используют его модификацию:
|
∞ |
|
∆wс = D x |
2Sм = ∫S( w)dw 2Sм |
(1.152) |
|
0 |
|
или |
∞ |
|
|
|
|
∆wс1 |
= ∫S2( w)dw 2Sм2 |
(1.153) |
|
0 |
|
Рассмотрим связь между этими двумя способами.
∞ ∞ ∞
∫S2( w)dw = ∫S( w)S( w)dw =< Sм∫S( w)dw .
0 0 0
С учетом этого неравенства :
∞ |
∞ |
∆wс1 ≤ Sм ∫S( w)dw Sм2 ; ∆wс1 ≤ ∫S( w)dw Sм . |
|
0 |
0 |
74
∞
но ∆wс = ∫S( w)dw 2Sм , ∆wс1 ≤ ∆wс .
0
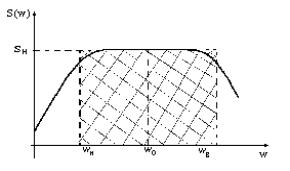
Это справедливо для любых сигналов. Еще одним способом определения частотного диапазона является так называемый метрологический подход. При этом подходе под частотным

диапазоном понимается такой, в котором СПМ S(w) незначительно отличается от своего наибольшего значения (в соответствии с рисунком 28).
Рисунок 28 - Метрологический подход к определению частотного диапазона
Координата пересечения линии, параллельной оси абсцисс и отстоящей от нее на Sм-δ, с кривой S(w) дают граничные частоты wн
и wв.
Sм-δ=S(w); |
1 − γ = SS( w) ; |
γ = 5-10%. |
||||
|
|
|
|
м |
|
|
1 − |
δ |
= |
S(w) |
|
(1.154) |
|
Sм |
Sм |
|||||
|
|
|
||||
Этот способ дает заниженные значения эквивалентной ширины спектра мощности.
В зависимости от того , в каком соотношении находятся между собой w0 и ширина спектра , различают два типа сигналов:
1)широкополосные, у которых ширина частотного диапазона значительно превышает значение основной частоты: ∆wс >> w0 ;
2)узкополосные , у которых основная частота намного больше эквивалентной ширины спектра мощности.
Укажем здесь еще одно свойство всех стационарных случайных процессов, которое носит названия соотношения неопределенности:
Произведение интервала корреляции случайного сигнала на
75
эквивалентную ширину спектра его мощности есть величина постоянная, значение которой зависит от способов задания этих
характеристик: |
|
τк ∆wс = const |
(1.155) |
Например, рассмотрим широкополосный сигнал с нулевой основной частотой w0=0, тогда Sм=S(0). Мы знаем, что
∞
∆wс = ∫S( w)dw 2Sм = D x 2Sм
0

w0 = 0,
∞
S(w) = 1π ∫R x (τ) cos( wτ)dτ,
0
∞∞
S(0) = 1π ∫R x (τ)dτ = Dπx ∫ρx (τ)dτ = D xπτк = Sм,
|
|
|
0 |
|
|
|
0 |
|
|
|
|
π |
|
|
∆w |
c |
= |
D x π |
= |
π |
; |
тогда ∆w |
c |
τ |
к |
= |
; |
||
2 |
||||||||||||||
2D x τк |
|
|||||||||||||
|
|
|
2τк |
|
|
|
|
|||||||
Рассмотрим теперь некоторые специальные виды сигналов .
Полосовые шумы
Полосовым шумом называется сигнал, СПМ которого постоянна в заданной полосе частот, а вне ее равна нулю (в соответствии с рисунком 29 и 30).
Рисунок 29 - Спектр узко- |
Рисунок 30 - Спектр широко- |
полосного сигнала |
полосного сигнала |
W0 - частота, делящая частотный диапазон пополам:
76
w0 = wн 2+wв .
S0 - интенсивность шума.
Основной частотой широкополосного сигнала считается нулевая частота.
Рассмотрим узкополосный шум. Выразим его интенсивность через дисперсию :
∆wсS0 = D x  2 - это площадь прямоугольника на рисунке 23,
2 - это площадь прямоугольника на рисунке 23,
S = |
D x |
= |
D x |
|
2( wв −wн ) |
||
0 |
2∆wc |
||

Рассмотрим функцию корреляции полосового шума.
∞ ∞
R x (τ) = ∫S( w) cos( wτ)dw = 2∫S( w) cos( wτ)dw =
−∞ |
0 |
|
wв |
|
|
|
|
|
|
wв |
|
|
|
|
|||
= 2 ∫S( w) cos( wτ)dw = 2 |
|
∫S0 cos( wτ)dw = |
|||||||||||||
|
wн |
|
|
|
|
|
|
wн |
|
|
|
|
|||
|
|
|
|
|
|
|
wв |
|
|
|
|
|
|
D x |
|
= 2D x 2( wв − wн ) ∫cos( wτ)dw = |
sin( wτ) |
||||||||||||||
wв −wн |
τ |
||||||||||||||
|
|
|
|
|
|
|
wн |
|
|
|
|
|
|
|
|
= |
|
D x 2 |
|
|
sin( wв −wн τ) cos( wв +wн |
τ); |
|
||||||||
|
τ( wв −wн ) |
2 |
|
|
|
|
|
|
2 |
|
|
||||
но wв |
− wн |
|
= ∆wc , (wв+wн )/2=w0, тогда |
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
∆w |
c 2 τ) cos(w0τ) |
||
или |
|
Rx(τ) = D x ∆wcτ sin( |
|
||||||||||||
|
|
|
|
|
|
sin(∆wc |
|
|
|
|
|
|
|
|
|
|
|
R |
x |
(τ) = D |
x |
2 |
τ) |
cos(w |
τ) |
|
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
∆wc τ |
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|wв =
wн
(1.156)
АКФ полосового шума имеет колебательный, затухающий характер. Рассмотрим вопрос: при каких условиях отсчеты шума будут некоррелированными? АКФ будет равной нулю, когда либо синус, либо косинус равны нулю:
а) sin(∆wc 2 τ) = 0 , когда
77
∆w c  2 τ = kπ, k=1,2,... (при k=0 значение АКФ равно единице);
2 τ = kπ, k=1,2,... (при k=0 значение АКФ равно единице);
τ = 2kπ ∆wc ; w = 2πf ; ∆wc = 2π∆fc, τ = k ∆fc . |
(1.157) |
Таким образом, отсчеты шума будут некоррелированными, если их брать через интервал 1 ∆fc ;
∆fc ;
б) cos(w0 τ)=0; w0 τ=(2k+1) π/2, k=0, 1, 2,...
τ = (2k +1)π 2w0 ; w0 = 2πf0;
τ = (2k +1)π 2 2πf0 = (2k +1) 4f0

Найдем шаг по аргументу : |
|
(2k+1)/4f0 - (2(k-1)+1)/4f0=(2k+1-2k+2-1)/4f0 =1/2f0 |
(1. 158) |
Таким образом, получены два шага дискретизации, при которых отсчеты сигнала становятся некоррелированными. Из них надо брать тот, который имеет наименьшее значение, для узкополосных сигналов это - ∆t =1/2f0 - наименьший шаг, при котором отсчеты некорелированы.
Рассмотрим теперь широкополосный шум.
wн=0; wв=∆wс .
Для определения АКФ сигнала воспользуемся формулой для функции корреляции узкополосного шума (1.121), положив wн=0.
Rx(τ) = D xτ sin(wвτ) = Dx sin(∆wcτ) ∆wcτ
wв
sin(∆wcτ) = 0;
∆wcτ = kπ; τ = kπ ∆wc = kπ 2π∆fc = k 2∆f
Шаг дискретизации по времени для некоррелированных отсчетов составляет
t=1/2 ∆fс.
(1.159)
c .
получения
(1.160)
Белый шум
Белый шум - это такой стационарный случайный сигнал, спектральная плотность мощности которого постоянна на любой частоте (в соответствии с рисунком 31).
78
Рисунок 31 - Спектр белого шума
Понятие белого шума аналогично понятию белого света, содержащего все спектральные составляющие. Белый шум представляет собой математическую абстракцию, так как площадь под прямой S(w)=S0 бесконечна (а следовательно, бесконечна и дисперсия, т. е. полная мощность сигнала).
|
|
|
∞ |
∞ |
R x (τ) = |
∫S( w) exp( jwτ)dw = S0 ∫exp( jwτ)dw = |
|||
|
|
|
−∞ |
−∞ |
|
|
|
∞ |
|
2πS0{ |
1 |
|
∫exp( jwτ)dw} = 2πS0δ(τ). |
|
2π |
||||
−∞
2 πS0=N - интенсивность белого шума (как уже отмечалось, о мощности белого шума говорить бессмысленно).
Итак, корреляционная функция белого шума имеет вид
Rx( τ)=Nδ ( τ), |
(1.161) |
по виду АКФ совпадает с дельта - функцией, и все ее свойства аналогичны свойствам дельта - функции:
τ = 0, τ ≠ 0 R x ( ) ∞, τ = 0
Отсчеты сигнала, являющегося белым шумом, взятые с любым шагом дискретизации, отличным от нуля, всегда некоррелированы. То есть, если имеется возможность генерировать белый шум, то не представляется сложным получать последовательности случайных
79
величин, не коррелированных во времени.
Если СПМ случайного сигнала постоянна в широком диапазоне частот, перекрывающем полосу пропускания динамической системы, то по отношению к этой системе данный
сигнал можно принять за белый шум. |
|
Иногда для на практике вводится нормированная СПМ: |
|
Sн(w)=S(w)/Dx |
(1.162) |
по аналогии с нормированной АКФ.

∞
R x(τ) = ∫S(w) exp( jwτ)dw
−∞
∞
S(w) = 21π ∫R x(τ) exp(−jwτ)dτ
−∞
Разделим левую и правую части на Dx, получим:
|
|
∞ |
|
|
|
|
|
ρx (τ) = |
∫Sн( w) exp( jwτ)dw |
||||||
|
|
−∞ |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
S ( w) = |
|
|
|
|
|||
1 |
∫ |
ρ |
x |
(τ) exp(−jwτ)dτ |
|||
|
|||||||
|
н |
|
2π |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
−∞ |
|
|
|
То есть нормированные СПМ и АКФ связаны между собой той же парой преобразований Фурье, что и ненормированные характеристики.
Все свойства нормированной спектральной плотности полностью аналогичны свойствам СПМ (четная, неотрицательная), кроме условия нормировки:
∞
∫Sн( w)dw = 1.
−∞
Неканоническая модель стационарного случайного сигнала (по Чернецкому)
Пусть имеем стационарный случайный сигнал X(t), который попытаемся описать моделью X(t), определяемую критериями
M[X(t)]=M[Xм(t)] |
(1.163) |
80 |
|
D[X(t)]=D[Xм(t)] |
(1.164) |
Rx( τ)=Rм( τ) |
(1.165) |
Модель стационарного случайного процесса можно |
|
предположить в следующем виде: |
|
X(t)=mx+b1sin(wt)+b2cos(wt), |
(1.166) |
где b1, b2, w - центрированные, независимые случайные величины. Эту модель можно представить в виде

X(t) = m x + 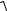 b12 + b22 sin( wt + arctg(b1 b2 )) .
b12 + b22 sin( wt + arctg(b1 b2 )) .
То есть, случайный процесс представляет аддитивную смесь постоянной составляющей и суммы гармоник со случайными амплитудами, частотами и фазами.
В данной модели компактность достигается за счет того, что частота носит случайный характер. В этом и заключается ее основное отличие от канонической модели Пугачева.
Для центрированного случайного сигнала модель имеет вид
ο
X(t) = b1sin(wt) + b2cos(wt) .
Найдем дисперсию модели
ο 2
D м = M [X м(t)];
ο 2
X м(t) = b12sin2(wt) + 2b1b2sin(wt)cos(wt) + b22cos2(wt) =
=b12sin2(wt) + b1b2sin(2wt) + b22cos2(wt) = b12sin2(wt) + b1b2sin(2wt) +
+b22 - b22sin2(wt) = (b12 - b22 )sin2(wt) + b22 + b1b2sin(2wt)
Всоответствии с этой формулой находим дисперсию:
D м = M[(b12 - b22)] M[sin2(wt)] + M[b22] + M[b1]M[b2]M[sin(2wt)] = = {M[b12] - M[b22]} M[sin2(wt)] + M[b22] + 0,
т. к. b1 и b2 центрированы.
Должно выполняться условие: Dм=Dx, то есть
81
|
{M [b2] - M [b2]} M [sin2(wt)] + M [b2] = D |
x |
|||
|
1 |
2 |
|
2 |
|
Левая часть не должна зависеть от времени. Это выполняется, |
|||||
когдаM [b2] = M [b2] , тогда M [b2] = D |
x |
, таким образом |
|||
1 |
2 |
2 |
|
|
|
|
M [b2] = M [b2] = D |
x |
|
(1.167) |
|
|
1 |
2 |
|
|
|
То есть, случайные величины, входящие в модель Чарнецкого, могут быть любыми, но непременно центрированными и с равными
дисперсиями, которые, в свою очередь, должны быть равны дисперсии моделируемого сигнала .
Напомним еще об одном требовании, которому должна удовлетворять модель - равенстве корреляционных функций исследуемого сигнала и модели:
R x (τ) = R м(τ)
ο |
ο |
ο |
|
R м(τ) = M [X м(t) X м(t − τ)]; X м(t) = b1 sin(wt) + b2 cos(wt); |
|||
ο |
|
|
|
X м(t − τ) = b1 sin(w(t − τ)) + b2 cos(w(t |
− τ)); |
||
οο
X |
м |
(t) X |
м |
(t − |
τ) = b2 sin(wt) sin(w(t − τ)) + b b |
2 |
sin(wt) cos(w(t − τ)) + |
|||||
|
|
|
|
|
|
1 |
|
1 |
|
|||
+ b b |
2 |
cos(wt) sin(w(t − τ)) |
+ b2 cos(wt) cos(w(t − τ)) |
|||||||||
|
|
1 |
|
|
|
|
|
M [b2 |
2 |
|
|
|
|
|
|
|
|
|
R |
м |
(τ) = |
]M [sin( wt) sin( w(t − τ))] + |
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
+M [b1]M [b2 ]M [sin( wt) cos( w(t − τ))] +
+M [b1]M [b2 ]M [cos( wt) sin( w(t − τ))] +
+M [b22 ]M [cos( wt) cos( w(t − τ))]
Но так как b1 и b2 являются центрированными случайными величинами, то их математические ожидания равны нулю, и тогда
R |
м |
(τ) = M [b2]M [sin( wt) sin( w(t − τ))] + |
|
|
1 |
|
|
M [b22]M [cos( wt) cos( w(t − τ))] = |
(1.168) |
||
= D xM [sin( wt) sin( w(t − τ))] + |
|
||
+ D xM [cos( wt) cos( w(t − τ))] = D xM [cos( wτ)]
Следует отметить, что данные функции корреляции удовлетворяют условию стационарности (не зависят от времени, но лишь от временного сдвига между сечениями процесса) и имеет
82
одинаковую с исследуемым сигналом дисперсию.
R x (τ) = D xM [cos( wτ)]
Зададимся теперь вопросом, как правильно выбрать значение частоты w?
Параметры же b1 и b2 выбираются из условия равенства дисперсий оцениваемого сигнала и модели.
Для этого разделим левую и правую части выражения для АКФ на Dx.

ρx (τ) = M [cos( wτ)]
Пусть f(w) - плотность вероятности распределения случайной величины w, тогда
∞
M[cos(wτ)] = ∫f (w) cos(wτ)dw
−∞
Но нормированная АКФ равна
∞
ρx(τ) = ∫f (w) cos(wτ)dw
−∞
Из этого интегрального уравнения можно найти плотность распределения f(w) случайной величины w .
Однако, памятуя о том, что нормированная спектральная плотность стационарного случайного процесса и его нормированная АКФ связаны друг с другом парой преобразований Фурье:
∞
Sн( w) = 21π ∫ρx (τ) cos( wτ)dτ
−∞
R x (τ) = D xM [cos( wτ)]
Корреляционная функция не зависит от выбора параметров b1 и b2, но лишь от случайной частоты w. Напрашивается вывод о том, что плотность распределения случайной величины w численно должна быть равна
f(w) = S (w) |
(1.169) |
83
То есть, случайные величины b1, b2 и w, входящие в модель Чернецкого, должны представлять собой центрированные и независимые случайные величины. При этом дисперсии величин b1 и b2 должны быть равными друг другу и равны дисперсии исследуемого сигнала.
Плотность распределения случайной величины w должна быть при этом равна нормированной спектральной плотности моделируемого сигнала.
Математическое описание систем случайных сигналов в частотной области

Пусть имеем два стационарных случайных сигнала X(t) и Y(t). Каждый из них характеризуется своей корреляционной функцией Rx( τ) и Ry( τ), а также функцией взаимной корреляции Rxy( τ).
Для описания свойств системы сигналов в частотной области используется взаимная спектральная плотность мощности (ВСП), которая определяется как преобразование Фурье от взаимной корреляционной функции:
|
|
|
|
∞ |
|
|
|
|
Syx (w) = |
1 |
∫R yx (τ) exp(−jwτ)dτ |
(1.170) |
|||
2π |
|||||||
|
|
|
|
−∞ |
|
|
|
Рассмотрим свойства ВСП: |
|
|
|||||
|
|
∞ |
∞ |
|
|||
Syx ( w) = |
1 |
∫R yx (τ) cos( wτ)dτ − j |
1 |
∫R yx (τ) sin( wτ)dτ |
(1.171) |
||
2π |
2π |
||||||
|
|
−∞ |
−∞ |
|
|||
Взаимная спектральная плотность является комплексной функцией своего аргумента, ее мнимая часть не равна нулю.
|
|
|
∞ |
ReSyx ( w) = |
1 |
∫R yx (τ) cos( wτ)dτ — вещественная часть ВСП, |
|
|
2π |
||
|
|
|
−∞ |
|
|
|
∞ |
I m Syx ( w) = |
1 |
∫R yx (τ) sin( wτ)dτ — мнимая часть ВСП . |
|
2π |
|||
|
|
|
−∞ |
Вещественная часть ВСП является четной, а мнимая - нечетной функцией частоты .
Syx (w) = ReSyx (w) - jImSyx (w) = ¦Syx (w)¦exp(-jϕ(w))¦,
84
где
¦Syx (w)¦= Re2Syx (w) + Im2Syx (w) - амплитудно-частотный спектр сигнала, четная функция частоты,
ϕ(w) = arctg(I mSyx (w) ReSyx (w)) - фазо-частотный спектр.
В формуле (1.170) вместо w подставим -w:

∞
Syx (−w) = 21π ∫R yx (τ) exp( jwτ)dτ.
−∞
В правой части переменную интегрирования заменим на - τ:
|
|
∞ |
|
|
||
Syx (−w) = |
1 |
∫R yx (−τ) exp(−jwτ)dτ, но |
Ryx(- τ)=Rxy( τ), |
|||
2π |
||||||
|
|
−∞ |
|
|
||
тогда |
∞ |
|
||||
|
|
|
|
|
|
|
Syx (−w) = |
1 |
|
∫R xy (τ) exp(−jwτ)dτ = Sxy ( w) |
|||
2π |
||||||
|
|
|
|
|
−∞ |
|
Таким образом, |
|
|
||||
|
|
|
|
|
Syx (−w) = Sxy ( w) |
(1.172) |
Взаимная спектральная плотность удовлетворяет свойству |
||||||
|
|
|
|
|
∞ |
|
R yx(τ) = |
∫Syx (w) exp( jwτ)dw |
(1.173) |
||||
−∞
То есть, взаимная корреляционная функция и ВСП связаны между собой парой преобразований Фурье.
85
Рисунок 32 - К определению ширины взаимного спектра
Та частота, на которой модуль ВСП достигает максимума, называется основной частотой взаимного спектра.
Весь взаимный спектр располагается вблизи этой частоты. Тот диапазон частот, в котором модуль взаимной спектральной плотности мало отличается от своего наибольшего значения, носит название частотного диапазона взаимного спектра .
Ширина его равна ширине взаимного спектра:
∆w = wв −wн |
(1.174) |
Определение ширины взаимного спектра
Ширина взаимного спектра может быть определена одним из двух следующих способов:
|
|
|
∞ |
|
|
|
1) ∆wв |
= |
∫|Syx ( w)|dw |
(1.175) |
|||
0 |
|
|||||
|Syx ( w)|max |
||||||
|
|
∞ |
|
|
|
|
2) ∆wв |
= |
∫|Syx ( w)|2 dw |
(1.176) |
|||
0 |
|
|
||||
|
2 |
|
||||
|
|
|
|Syx ( w)|max |
|
||
Второй способ получил большее распространение, так как первый интеграл часто расходится.
Взаимный спектр несет информацию о взаимосвязи сигналов в частотной области. Наибольшая такая взаимосвязь наблюдается при частоте w0.
Ширина взаимного спектра указывает на тот частотный диапазон, где взаимосвязь между сигналами достаточно велика.
Анализ линейных динамических систем, работающих при входных случайных воздействиях
Пусть имеем ЛДС с импульсной переходной характеристикой
86
h( τ), на вход которой поступает случайный процесс X(t).
Надо уметь находить выходной сигнал и определять все его свойства, если известны характеристики входного сигнала, т. е. Находить
M[Y(t)], D[Y(t)], Ry(t,t+ τ), Ryx(t.t+ τ).
Они будут зависеть от свойств входного сигнала и характеристик ЛДС.
t |
|
Y(t) = ∫h(τ)X(t - τ)dτ |
(1.177) |
0 |
|
t |
t |
1)M[Y(t)] = M[∫h(τ)mx(t - τ)dτ] = ∫h(τ)M[X(t - τ)]dτ
|
|
t |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
M [Y(t)] = ∫h(τ)mx(t - τ)dτ = my(t) |
(1.178) |
|||||
|
|
0 |
|
t |
|
|
|
|
ο |
|
|
|
|
|
|
2) Y(t) = Y(t) − m y (t) = ∫h(τ){X(t - τ) - m x (t - τ)}dτ, |
|||||||
|
|
|
|
t |
0 |
|
|
|
|
ο |
|
ο |
|
|
|
|
|
Y(t) |
= ∫h(τ) X(t - τ)dτ |
|
(1.179) |
||
|
|
t+ u |
|
0 |
|
|
|
|
ο |
|
ο |
|
|
|
|
3) |
Y(t + u) = |
∫ |
h(τ1) X(t + u - τ1)dτ1 , |
|
|||
|
|
0 |
|
|
|
|
|
ο |
ο |
t t +u |
|
ο |
ο |
|
|
Y(t) Y(t + u) |
= ∫ |
∫ |
h(τ)h(τ1) X(t - τ) X(t + u - τ)dτdτ1 ; |
||||
|
|
0 |
0 |
|
|
|
|
Находим математические ожидания левой и правой частей:
t |
t +u |
|
R y(t, t + u) = ∫ |
∫ h(τ)h(τ1)R x(t - τ1, t + u - τ)dτdτ1 . |
(1.180) |
0 |
0 |
|
Найдем дисперсию выходного сигнала, для этого положим
u=0:
t t |
|
D[Y(t)] = ∫ ∫ h(τ)h(τ1)R x (t - τ1, t - τ)dτdτ1 |
(1.181) |
0 0 |
|
87
то есть, чтобы отыскать дисперсию выходного сигнала, необходимо знать АКФ входного.
4)Взаимная корреляционная функция:
ο |
ο |
R yx (t, t + u) = M [ Y(t) X(t + u)] = |
|
t |
(1.182) |
= ∫ h(τ)R x (t - τ, t + u - τ)dτ
0
Выходной сигнал стационарной ЛДС при входном нестационарном сигнале будет нестационарным.
Иногда используют следующий подход. Входной сигнал представляют в виде канонической модели
∞
X(t) = m x (t) + ∑U kϕk (t) ,
k =1
тогда выходной сигнал:
t |
∞ |
t |
Y(t) = ∫ h(τ)m(t + τ)dτ + ∑ U k ∫ h(τ)ϕk (t − τ)dτ; |
||
0 |
k=1 |
0 |
|
t |
|
ψk(t) = ∫h(τ)ϕk(t − τ)dτ; |
|
|
|
0 |
|
|
∞ |
|
Y(t) = m y (t) + ∑U k ψk (t) |
(1.183) |
|
k =1
Если на входе линейной динамической системы имеем каноническую модель входного сигнала, то на выходе получаем каноническую модель выходного сигнала с теми же коэффициентами разложения. Отличаются только координатные функции.
Пусть входной сигнал является стационарным. Рассмотрим характеристики выходного сигнала системы.
t |
t |
|
m y (t) = ∫h(u)m x (u)du = m x ∫h(u)du |
(1.184) |
|
0 |
0 |
|
Вывод: выходной сигнал стационарной ЛДС при
88
стационарном входном сигнале не стационарен по математическому ожиданию.
|
t t |
|
D y(t) = ∫ ∫ h(τ)h(τ1)R x (τ, τ1)dτdτ1 |
(1.185) |
|
|
0 0 |
|
t |
t +u |
|
R y (t, t + u) = ∫ |
∫ h(τ)h(τ1)R x (u - τ1 + τ)dτdτ1 . |
(1.186) |
0 |
0 |
|

По автокорреляционной функции выходной сигнал не стационарен при стационарном входном.
Взаимно-корреляционная функция:
t |
|
R yx (t, t + u) = ∫ h(τ)R x (u + τ)dτ . |
(1.187) |
0 |
|
То есть, входной и выходной сигналы нестационарно связаны. Рассмотрим теперь установившийся (статический) режим работы ЛДС, устремив верхний предел интегрирования к
бесконечности.
|
∞ |
|
1) m y |
= m x ∫h(u)du |
(1.188) |
|
0 |
|
|
∞ ∞ |
|
2) D y |
= ∫ ∫ h(τ)h(τ1)R x (τ1 - τ)dτdτ1 |
(1.189) |
|
0 0 |
|
|
∞ ∞ |
|
3) R y (u) = ∫ ∫ h(τ)h(τ1)R x (u - τ1 + τ)dτdτ1 |
(1.190) |
|
|
0 0 |
|
|
∞ |
|
4) R yx (u) = ∫ h(τ)R x (u + τ)dτ |
(1.191) |
|
|
0 |
|
В установившемся режиме работы выходной сигнал ЛДС при стационарном входном является стационарным и стационарно связанным со входным.
Спектральная плотность мощности выходного сигнала определяется выражением
∞
Sy (w) = 1π ∫R y(u) exp(−jwu)du ,
2 −∞
89
Подставим сюда выражение для АКФ:
|
∞ ∞ |
|
1 |
∞ |
R |
|
(u - τ |
+ τ)exp(-jwu)du}dτdτ |
S ( w) = ∫ ∫ h(τ)h(τ ){ |
∫ |
|
||||||
|
|
|||||||
y |
0 0 |
1 |
2π −∞ |
|
x |
1 |
1 |
|
Рассмотрим интеграл в скобках:

u − τ1 + τ = u1 |
|
|
∞ |
||||
|
|
||||||
u = u1 + τ1 − τ |
1 |
||||||
∫R x (u) exp(−jw(u + τ1 − τ))du = |
|||||||
du = du |
|
|
|
π |
|||
|
1 |
|
|
2 |
−∞ |
||
u1 |
= ∞; u2 |
|
= −∞ |
|
|
||
н |
|
|
|
||||
в |
|
|
|
|
|||
∞
= exp( jwτ) exp(−jwτ1) 21π −∞∫R x (u) exp(−jwu)du = = Sx ( w) exp( jwτ) exp(−jwτ1)
- подставим в исходный интеграл:
∞ ∞
Sy ( w) = Sx (w) ∫ ∫ h(τ)h(τ1)exp(-jwτ1)exp(jwτ)dτdτ1 =
0 0
∞ ∞
= Sx ( w){ ∫ h(τ1)exp(-jwτ1)dτ1}{ ∫ h(τ)exp(jwτ)dτ} = |
|
0 |
0 |
= Sx ( w)W( jw)W(−jw) = Sx ( w)| W( jw)|2 .
(1.192)
То есть, спектральная плотность мощности выходного сигнала ЛДС при подаче на нее стационарного случайного сигнала связана с СПМ входного сигнала через квадрат модуля частотной характеристики.
Если искать дисперсию, АКФ и ВКФ по соотношениям (1.189), (1.190) и (1.191), то придется иметь дело с двойными интегралами, в то время как эти характеристики можно найти проще, пользуясь найденной зависимостью (1.192):
∞∞
D y = ∫Sy ( w)dw = |
∫Sx ( w)|W( jw)|2 dw , |
(1.193) |
−∞ |
−∞ |
|
то есть дисперсия, также как и СПМ, зависит не от всей частотной
90
характеристики, а только от АЧХ.
∞
R y (τ) = ∫Sy (w) exp( jwτ)dw =
−∞ |
(1.194) |
|
∞ |
||
|
||
= ∫Sx (w)|W( jw)|2 exp( jwτ)dw. |
|
|
−∞ |
|
Рассмотрим какое практическое применение имеет найденная
зависимость. Спектр выходного сигнала зависит от СПМ входного и амплитудно-частотной характеристики системы.
Пусть на вход ЛДС подается белый шум, тогда
Sy(w)=S0=const, |
|
Sy(w) =S0¦W(jw)¦2 , |
(1.194) |
то есть СПМ выходного сигнала зависит только от квадрата модуля частотной характеристики системы. Меняя частотную характеристику, можно получать сигналы с различными спектрально-корреляционными свойствами, окрашенные шумы. Это очень важный вывод, так как многие задачи планирования эксперимента решаются имитационным моделированием, которое предполагает, в свою очередь, использование в качестве исследуемых сигналов случайных процессов с заданными спектральными характеристиками (для проверки свойств синтезируемых фильтров, систем, и т. д. ).
∞ |
|
R yx (u) = ∫ h(τ)R x (u + τ)dτ |
(1.195) |
0 |
|
Пусть мы определили АКФ входного сигнала и функцию взаимной корреляции между входным и выходным сигналами. Соотношение (1. 195) можно использовать для определения ИПХ исследуемой системы. Найдем ВКФ между входным X(t) и выходным Y(t) сигналами системы, заменив в соотношении (1.195) у аргумента u знак на противоположный:
∞ |
|
R yx (−u) = ∫ h(τ)R x (-u + τ)dτ |
(1.196) |
0 |
|
∞ |
|
R xy (u) = ∫ h(τ)R x (u - τ)dτ |
(1.197) |
0 |
|
91
Пусть на вход системы подается стационарный белый шум. Его корреляционная функция:
R x (τ) = N δ(τ), R x (u − τ) = N δ(u − τ) ,
∞
R xy (u) = N ∫ h(τ)δ(u - τ)dτ
0

Согласно фильтрующему свойству дельта - функции:
R xy (u) = N h(u) ,
то есть вид ВКФ совпадает с видом импульсной переходной характеристики ЛДС.
h(u) = R xy (u) |
N |
(1.198) |
|
|
Соотношение (1.198) можно использовать как алгоритм определения ИПХ.
Далее подается тестовый сигнал - белый шум и вычисляется взаимная спектральная плотность входного и выходного сигналов.
|
|
|
|
|
|
1 |
|
∞ |
|
|
|
|
|
|
|
|
|
Sxy(w) = |
|
∫Rxy(u) exp(−jwu)du = |
|||||||||||
|
2π |
||||||||||||||
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
∞ |
|
1 |
|
∞ |
|
|
|
|
|
|
||
|
|
= ∫h(τ){ |
|
∫Rxy(u − τ) exp(−jwu)du}dτ |
|||||||||||
|
2π |
||||||||||||||
|
|
|
0 |
|
|
|
|
|
−∞ |
|
|
|
|
|
|
Внутренний интеграл: |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∞ |
|
|
−jw( u1 |
+τ) |
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
u − τ = u1 |
|
u |
= ∞ |
2π |
|
|
∫R x (u1)e |
|
du1 |
= |
|||||
|
|
|
|
||||||||||||
u = u + τ |
|
1в |
|
|
|
|
−∞ |
|
|
|
|
|
|
||
1 |
|
u1н |
= −∞ |
|
|
|
− jwτ 1 |
∞ |
|
|
|
||||
du = du |
|
|
|
|
−jwu1 |
−jwτ |
|||||||||
|
|
|
|
|
|
||||||||||
1 |
|
|
|
= e |
|
|
|
∫R x (u1)e |
|
du1} = e Sx ( w), |
|||||
|
|
|
|
{2π |
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
подставляем в исходный интеграл:
92
∞
Sxy(w) = Sx(w)∫h(τ) exp(−jwτ)dτ = Sx(w) W( jw) (1.199)
0
То есть взаимная спектральная плотность между входным и выходным сигналами связана с СПМ входного сигнала через частотную характеристику системы.
Вещественная частотная характеристика оказывает влияние на
вещественную часть ВСП и не оказывает влияния на мнимую часть ВСП, и наоборот.
Вывод: частотную характеристику системы можно определять, зная взаимную спектральную плотность входного и выходного сигналов, а также СПМ входного сигнала.
W( jw) = |
Sxy ( w) |
(1.200) |
|
S ( w) |
|||
|
|
||
|
x |
|
Любой сигнал можно представить как аддитивную смесь полезного сигнала и помехи:
ο
X(t) = S(τ) + X(t)
Выходной сигнал системы:
ο
Y(t) = my(t) + Y(t)
ЛДС осуществляет преобразование, причем
∞
m y (t) = ∫h(τ)S(τ)dτ, D y
0
(1.201)
(1.201)
ο
= D[Y] ,
Dy=min - условие минимума помехи.
Зададимся вопросом, что надо сделать для того, чтобы значение дисперсии выходного сигнала понизилось (а значит и уменьшилось значение помехи)?
∞ |
∞ |
|
∞ |
93 |
|||||
|
|
|
|||||||
D y = ∫ Sy (w)dw = |
∫ Sx (w) |
|
W( jw) |
|
2 dw = 2∫ Sx (w) |
|
W( jw) |
|
2 dw |
|
|
|
|
||||||
−∞ |
−∞ |
0 |
|
|
|
|
|||
|
|
|
|
(1.202) |
|||||
Пусть максимальное значение СПМ входного сигнала Sxн ,
тогда S(w) <= Sхн .
∞ |
|
∞ |
|
|
|
||||
D y = 2∫Sx (w) |
|
W( jw) |
|
2 dw ≤ 2Sxн ∫ |
|
W( jw) |
|
2 dw |
(1.203) |
|
|
|
|
||||||
0 |
|
|
0 |
|
|
|
|
|
|
Это — оценка дисперсии сверху, то есть оценка той величины, которой она не превышает.
ο
Пусть эквивалентная ширина спектра мощности сигнала X (t)
будет |
|
|
|
|
|
|
|
|
|
|
|
|
D x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆w c |
= |
|
|
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2Sн |
|
|
|
|
|
|
|
|||||
Пусть ширина полосы пропускания ЛДС определяется |
|||||||||||||||||||||||||
выражением |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dw |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
∫ |
|
W( jw) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
∆w ф = |
0 |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||
|
|
|
|
|
W( jw) |
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
D x |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 dw = ∆w |
|
|
|
|
2 |
|
|||||||||
S = |
|
, |
∫ |
|
W( jw) |
|
ф |
|
W( jw) |
|
, |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
хн |
2∆w |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим это в выражение для дисперсии (1.203):
2D x |
∆w ф |
|
W( jw) |
|
2 |
= D x |
|
W( jw) |
|
2 |
∆w ф |
, |
||||||
|
|
|
|
|||||||||||||||
2∆w c |
|
|
|
|
|
|
∆w c |
|||||||||||
|
|
|
|
|
|
|
|
|
|
∆w ф |
|
|
|
|
|
|||
D y |
≤ D x |
|
W( jw) |
|
|
|
|
|
|
(1.204) |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
∆w c |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение (1.204) определяет оценку сверху дисперсии выходного сигнала.
Выводы:
1)Мощность выходной помехи тем больше, чем больше
94
мощность входной помехи.
2)Ширину полосы пропускания ЛДС нужно делать как можно меньше ширины спектра мощности сигнала, стремиться к тому, чтобы отношение ∆wф / ∆wс было как можно меньше.
Перепишем соотношение по-другому:
τu ∆w ф = const ; τk ∆w с = const
|
∆w ф |
= |
τk |
= const ; |
|
|
∆w ф |
= C |
τu |
|
|||||
|
|
|
|
|
|
|
|
τk |
|||||||
|
∆w c |
τu |
|
|
∆w c |
||||||||||
C — константа, которая зависит от способа задания величин |
|||||||||||||||
∆wф, ∆wc, τu , τk . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
D y = C D x |
|
W( jw) |
|
2 τ |
u |
. |
(1.205) |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
τk |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
Соотношения (1.204) и (1.205) используются на равных основаниях.
Вывод: для наилучшего подавления помехи нужно увеличивать длительность ИПХ системы по сравнению с интервалом корреляции исследуемого процесса. Но увеличивая длительность ИПХ, мы ухудшаем быстродействие.
Нормализация стационарных случайных процессов линейными динамическими системами
Пусть X(t) — стационарный случайный сигнал с произвольным законом распределения. Он подается на вход ЛДС с импульсной переходной характеристикой h( τ).
В установившемся режиме работы выходной сигнал системы определяется выражением
∞ |
|
|
h(τ), |
0 ≤ τ ≤ τu |
Y (t) = ∫ h(τ)X (t − τ)dτ, |
|
|||
h(τ) = |
|
|||
0 |
|
|
0, |
τ > τu |
τu — длительность ИПХ, то есть |
|
|
|
|
|
τu |
|
|
|
Y(t) = |
∫ h(τ)X(t − τ)dτ. |
|
(1.206) |
|
|
0 |
|
|
|
Разобьем τu |
на отдельные |
промежутки ∆ (шаг |
||
дискретизации) N = τu / ∆ — число промежутков разбиения.
95
Для дискретизированного по времени сигнала процесс на выходе системы определится соотношением
N |
|
Y (t) = ∑h(k∆)X (t − k∆) |
(1.207) |
k =1
Выберем шаг дискретизации, равный τk , тогда N = τu / τk ,
N |
|
Y(t) = ∑h(kτk )τky X(t − kτky ) , |
|
k =1 |
|
Yk = h(kτk )X(t − kτk ) , |
(1.208) |
или |
|
N |
|
Yk = C k X(t − kτk ) , Y = ∑Yk , |
(1.209) |
k =1
то есть выходной сигнал представляется в виде суммы случайных величин. Определим свойства этих величин.
Yk = C k X(t − kτk )
ο |
ο |
Y k |
= C k X(t − kτk ) |
Рассмотрим другое сечение сигнала :
ο |
ο |
Y m |
= C m X(t − mτk ) |
и корреляционный момент между ними:
|
ο |
ο |
|
R[Yk , Ym ] = M Y k Y m |
|||
|
|
|
|
= C k C m R[(m − k)τ
|
ο |
ο |
|
= |
= C k C m M X(t − kτk ) X(t − mτk ) |
||||
|
|
|
|
|
2m R(0) = C 2m D y , k = m k ≠ m
То есть Ry( τk ),Ry(2 τk ), ... = 0 при k ≠ m , таким образом отсчёты Y некоррелированы.
N |
|
|
τu |
|
|
|
|||
Y (t) = ∑Yk , пусть N = |
→ ∞ ,тогда по центральной |
||||||||
|
|||||||||
k =1 |
|
|
τk |
|
|
||||
предельной теореме Ляпунова |
|
|
|
|
|||||
lim f(y) = f(y) |
|
|
(1.210) |
||||||
N = |
τu |
, |
τu |
→ ∞, |
τu |
→ 0. |
|||
|
|
|
|||||||
|
τk |
τk |
|
|
τk |
||||
Если длительность ИПХ системы намного превышает значение интервала корреляции входного сигнала, то закон распределения выходного сигнала можно считать нормальным при любом законе распределения входного. Чем больше, тем лучше
нормализация и, естественно, тем хуже быстродействие.
τu ∆w n = const ; |
τk ∆w с = const |
||||
|
τu |
= C |
|
∆w n |
. |
|
|
|
|||
|
τk |
|
∆w c |
||
То есть, чем уже полоса пропускания ЛДС по сравнению с эквивалентной шириной спектра мощности входного сигнала, тем лучше эта система осуществляет нормализацию.
Вопросы синтеза оптимальных ЛДС
При постановке задачи синтеза оптимальной системы прежде всего необходимо выбрать критерий оптимальности, задать, в каком смысле данная система является оптимальной. Таких критериев может быть много, например:
1)Dy = min - критерий минимума дисперсии помехи;
2)Dy/Dx = min - критерий наилучшей помехозащищенности;
3)пусть Yu(t) — идеальное значение выходного сигнала, величина Y(t) – Yu(t) характеризует отклонение поведения системы от идеала, для практических целей ее использовать неудобно, так
как она знакопеременна, поэтому воспользуемся другой, положительной: {Y(t) – Yu(t)}2 , но она случайна, так что для характеристики отклонения возьмем ее математическое ожидание:
M {Y(t) − Yu (t)}2 = ∆ — среднеквадратическая |
||||
|
|
|
|
|
|
|
|
|
|
погрешность. |
∆ = min |
|
|
(1.211) |
|
|
|
||
Соотношение |
(1.211) |
определяет |
так |
называемый |
среднеквадратический критерий. |
|
|
|
|
Кроме перечисленных критериев можно использовать |
||||
интегральный среднеквадратический критерий: |
|
|
||
∞∫ M [{Y (t) − Yu (t)}2 ]dt = min , |
|
97 |
||
|
(1.212) |
|||
0 |
|
|
|
|
критерий максимального быстродействия и пр. Можно решать две оптимизационные задачи:
1)параметрическая оптимизация;
2)строгая оптимизация.
Поставим задачу в общем виде. Есть полезный сигнал S(t),
ο
который искажается аддитивной помехой X (t) , то есть входной сигнал имеет вид:
ο
X(t) = S(t) + X (t) .
В идеале выходной сигнал определяется выражением
∞ |
|
Yu (t) = ∫ h(τ)S(t − τ)dτ |
(1.213) |
0 |
|
В качестве критерия адекватности будем использовать критерий минимума среднеквадратической погрешности.
Определим вид импульсной переходной характеристики
системы h(τ) , исходя из условия ∆= min, а далее по |
h(τ) станем |
||
строить структуру ЛДС. |
|
||
∞ |
|
||
Y(t) = ∫h(τ)X(t − τ)dτ |
|
||
0 |
|
||
∆- функционал от τ. |
|
||
Пусть h0(τ) - ИПХ оптимальной системы. |
|
||
∞ |
|
||
Y0(t) = ∫h0(τ)X(t − τ)dτ |
(1.214) |
||
0 |
|
|
|
Задачу будем решать методом неопределенных множителей |
|||
Лагранжа: |
|
||
h(τ) = h0(τ) + λh n (τ), |
(1.215) |
||
98 |
|
|
|
здесь λ - произвольная величина, − ∞ < λ < ∞- , |
|
||
h n (τ) -произвольная функция. |
|
||
h(τ) |
|
λ=0 = h0(τ) , |
|
|
|
||
|
|
||
Y(t) = Y0(t) + λYn (t) |
|
||
∞ |
|
||
где Yn (t) = ∫h n (τ)X(t − τ)dτY (t) |
(1.216) |
||
0
∆ = M [{Y0(t) + λYn (t) − Yu (t)}2 ] |
(1.217) |
||||
Рассмотрим ∆ как функционал от λ : ∆ = f (λ) , |
|
||||
|
|
∂∆ |
|
|
|
|
|
|
|
||
∆ |
|
λ=0 = M [{Y0(t) − Yn (t)}2 ]= ∆min ∂x |
|
λ=0 |
= 0 |
|
|||||
|
|
|
|
||
Если это условие выполняется для любых h n (τ) , то h0(τ) - ИПХ оптимальной системы.
∂∆∂∆ = M [2{Y0(t) + λYn (t) − Yu (t)}Yn (t)] = 0,
но λ = 0,тогда
∂∆ |
|
= M [{Y0(t) − Yu (t)}Yn (t)] = 0, |
|
||
∂∆ |
|
|
|
λ=0 |
M [Y0(t)Yn (t)]− M [Yn (t)Yu (t)] = 0.
Подставим выражения для Y0(t) (1.214) и Yn(t) (1.216):
∞ ∞
|
Y0(t)Yn (t) = ∫ ∫h0(u)h n (τ)X(t − u)X(t − τ)dudτ, |
|
0 0 |
|
∞ ∞ |
|
Yn (t)Yu (t) = ∫ ∫h0(u)Yn (t)X(t − u)du, |
|
0 0 |
∞ ∞ |
∞ ∞ |
∫ ∫h0(u)hn (τ)X(t − u)X(t − τ)dudτ- ∫ ∫h0(u)Yn (t)X(t − u)du =0
0 0 |
|
|
0 0 |
|
|
∞ |
|
∞ |
|
|
|
∫ |
|
|
∫ |
h0(τ)M [X(t − τ)X(t − u)]dτ − M [Yu (t)X(t |
|
|
|
|
|||
|
h n (u) |
|
− u)] du = 0 |
||
0 |
|
0 |
|
|
|
Это условие выполняется при любом виде h n (τ) ,если |
99 |
||||
внутренний |
|||||
интеграл равен нулю. |
|
||||
∞ |
|
|
|
|
|
∫h0(τ)M [X(t − τ)X(t − u)]dτ − M [Yu (t)X(t − u)]=0 |
(1.218) |
||||
0 |
|
|
|
|
|
Это - условие синтеза оптимальных динамических систем, из

его определяется h(τ) -оптимальная ИПХ. Уравнение (1.218) справедливо как для стационарных, так и для нестационарных случайных сигналов.
В частном случае, когда полезный сигнал и помеха стационарны, математические ожидания, стоящие в левой части, не будут зависеть от времени, а лишь от разности временных аргументов.
M [X(t − u)X(t − τ)] = ψ(τ − u) = ψ(u − τ) |
(1.219) |
M [Yu (t)X(t − u)] = γ(u) |
(1.220) |
В этом случае наше уравнение примет вид: |
|
∞ |
|
∫h0(τ)ψ(u − τ)dτ = γ(u) |
(1.221) |
0 |
|
Это - классическое уравнение Винера-Хопфа. Оно имеет совершенно определенную физическую интерпретацию и может быть решено в явном виде, тогда величина ψ (t) рассматривается как
входной сигнал динамической системы, а γ (t) - как выходной.
В изображениях Лапласа соотношение между этими величинами будет выглядеть как
γ(p) = W(p)ψ(p) , отсюда W(p) = ψγ((pp)) ,
где :
∞
γ(p) = ∫exp(−pu)γ(u)du;
0
∞
ψ(p) = ∫ψ(u) exp(−pu)du.
0
Положим τ= 0 , тогда
M [X(t)X(t − u)] = ψ(u);
(1.222)
M [Yu (t)X(t − u)] = γ(u).
Итак, если на вход системы подается аддитивная смесь
ο
полезного сигнала и помехи X(t)=S(t)+ X(t) , то для синтеза
оптимальной системы необходимо знать: сам полезный сигнал S(t), автокорреляционную функцию помехи, кроме того, нужно достаточно определенно знать, что именно мы хотим на - Yu(t). По этим данным можно найти функции γ(u) и ψ(u) . Затем находим
изображения по Лапласу γ(p) и ψ(p) . По этим изображениям
отыскиваем передаточную функцию W(p) оптимальной системы, на основе которой и осуществляется ее техническая реализация.
