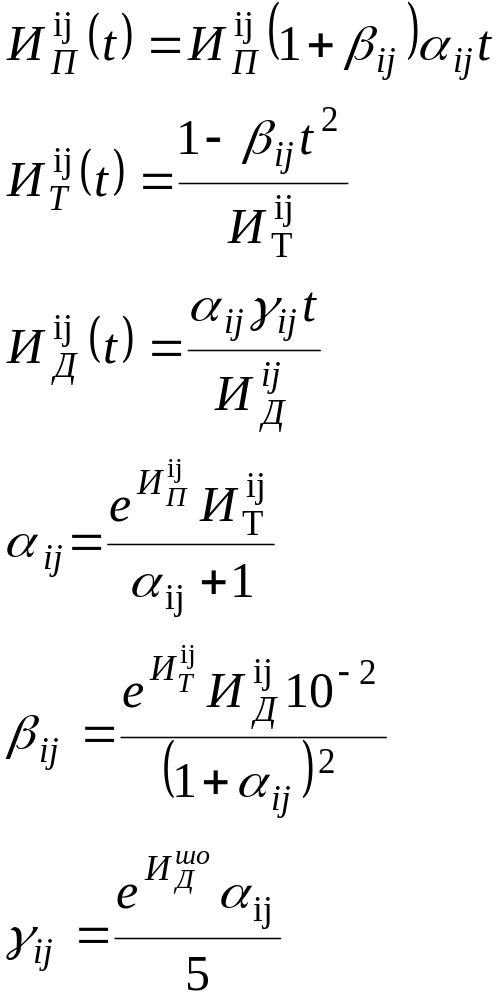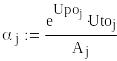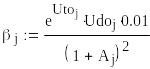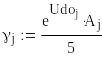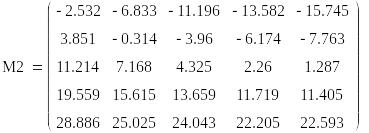
2. Найдем значения целевой функции f12(X,y) с учетом факторов риска

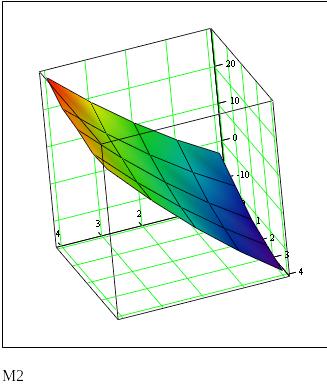
Найдем наиболее вероятную ситуацию:

Определим вероятности наступления каждой из пяти ситуаций

Следовательно наиболее вероятная ситуация S2 (y=1)

То есть при y=1 целевая функция f(x,y) максимальна при х=4

3. Сравним значения целевых функций с учетом и без учета факторов риска

Изобразим графически разность значений f(x,y) и F12(x,y)

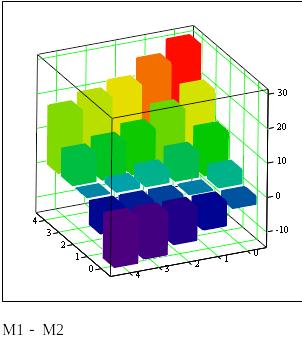
Не для всех значений переменных х и у значение целевой функции f(x,y) будет больше значений целевой функции F12(x,y)

Лабораторная работа 7 информационный анализ системных задач

Цель работы: провести информационный анализ ситуации. Изучить приемы и методы оценки влияния информированности на степень и уровень риска в задачах системного анализа. Провести ранжирование ситуаций по уровню опасности перехода их в чрезвычайные.

Теоретические сведения

Целью информационного анализа, как составной части одной и процедур системного анализа, является: установить основные свойства и понятия, дать определения количественных и качественных характеристик информации с позиции системного анализа. Рассмотреть пути и приемы получения информации и проанализировать методы оценки количественных и качественных характеристик информации. Изучить приемы и методы оценки влияния информированности на степень и уровень риска в задачах системного анализа [5–7].

Понятие количества и качества информированности

Количество информации по Шеннону: – энтропия, как мера неопределенности полной группы случайных событий или ситуаций. Величину можно рассматривать как меру неопределенности множества, которое содержит событий с вероятностями .

Под информированностью ЛПР будем понимать изменение уровня неопределенности знаний о ситуации или предмете анализа в результате получения информации.

Уровень информированности ЛПР – это показатель уровня знаний о предмете анализа или исследования. Количественно уровень информированности ЛПР будет характеризоваться величиной изменения уровня неопределенности в результате получения информации. При этом с получением информации уровень неопределенности может уменьшаться, если информация точная, но может и возрастать, если информация намеренно искажена или недостоверна, или противоречащая имеющейся информации.

Неопределенность ситуации оценивается с позиций целей системного анализа, т.е. с позиций степени и уровня риска и для каждой ситуации характеризуется многофакторно:

• неопределенность знаний о возможности совершения той или иной ситуации;

• неопределенность знаний о качестве имеющейся и вновь получаемой информации;

• неопределенность знаний о степени влияния той или иной ситуации на уровень риска.

Как качественные характеристики рассматриваются: неточность, неполнота, несвоевременность, недостоверность, неопределенность, противоречивость, нечеткость информации.

Неопределенность – свойство, которое указывает на наличие нескольких конкурирующих описаний ситуации.

Неточность – свойство, которое указывает на наличие определенного интервала допуска или погрешности в измерениях или расчетах количественных параметров и качественных характеристик описания ситуации.

Неполнота – это свойство, которое указывает на наличие информационных пробелов в описании ситуации.

Нечеткость – свойство, которое характеризует расплывчатость в описании ситуации при которой невозможно точно указать наличие или отсутствие определенного свойства или его точную количественную характеристику.

Несвоевременность – свойство, которое характеризует соотношение во времени между моментом наступления какого–то события и моментом получения информации о нем.

Недостоверность – свойство, которое указывает на наличие количественных данных или качественных характеристик, которые не соответствуют истинному состоянию ситуации.

Противоречивость – свойство, которое указывает на наличие количественных или качественных характеристик, которые имеют значения или смысл противоречащий другим данным.

Формализация характеристик информированности: полноты, достоверности, своевременности

Полнота информированности свойство, которое характеризует соответствие количество получаемой ЛПР информации количеству информации требуемой для принятия решения.

Показатель полноты информированности:

,

где – объем информации полученный ЛПР в складывающейся ситуации,

– соответственно максимально целесообразный и минимально допустимый объем информации для принятия решения.

–определяет уровень полноты информированности, что показывает насколько уровень полученной информации превышает минимально допустимый.

Своевременность информированности свойство, которое определяет насколько ресурс времени ЛПР на формирование и принятие решения соответствует ресурсу времени от момента получения информации. Показателем своевременности информированности будем называть соотношение между временным ресурсом формирования решения и временным ресурсом реализации решения:

,

где – длительность периода от момента начала формирования решения до момента его реализации; – длительность периода от момента начала формирования решения до момента его завершения; – минимально возможная длительность периода формирования решения для заданного множества ситуаций; –максимально целесообразная длительность периода формирования решения для заданного множества ситуаций.

Достоверность информированности свойство, которое характеризует соответствие полученной ЛПР информации истинному состоянию складывающейся ситуации.

Показатель достоверности информации:

,

где – уровень достоверности информации о рассматриваемой ситуации; – соответственно максимально теоретически целесообразный и минимально практически целесообразный, при котором можно принимать решение, уровень достоверности информации в заданном множестве ситуаций.

Интегральный показатель информированности и его особенности

Перечислим важные свойства информированности. Уровень информированности возрастает непрерывно при увеличении каждого из частных показателей, или любого из них.

Повышение общего уровня информированности ЛПР при увеличении показателей происходит по нелинейному закону: прирост уровня информированности постепенно замедляется при приближении к граничному значению их показателей.

Уровень информированности при понижении значения одного из показателей ниже определенного порогового значения не может быть компенсирован за счет увеличения других показателей.

При нулевом значении любого из показателей общий уровень информированности так же равен 0.

Интегральный показатель информированности включает количественные и качественные характеристики:

,

где

Постановка задачи информационного анализа.

При принятии решения необходимо найти рациональный компромисс между уровнями в динамике формирования решения с целью сокращения времени на его формирование.

При этом .

t

ИД

ИП

ИТ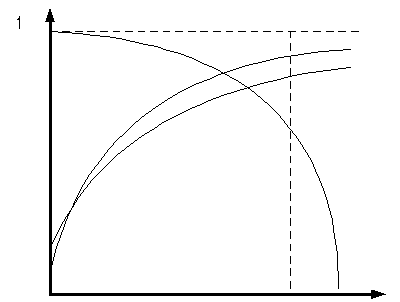

Рис. 7.1. Зависимость перехода ситуации в чрезвычайную от набора воздействующих факторов

Задача классификации и ранжирования ситуации.

Под действием множества неконтролируемых факторов критическая ситуация может перейти в чрезвычайную. Переход ситуации в чрезвычайную зависит от набора воздействующих факторов (табл. 7.1). В таблице 7.1 «+» означает, что под действием соответствующего фактора критическая ситуация переходит в чрезвычайную. «–» – означает, что фактор риска не влияет на ситуацию. Вероятность события, при котором под воздействием фактора ситуация может перейти в чрезвычайную зависит от полноты информированности. Данная зависимость записывается в виде:

,

где – коэффициент (табл. 7.2), – полнота информированности (табл. 7.3).

Таблица 7.1

	1	2	3	4	5	6	7
1	+	+	+	+	–	+	+
2	–	–	+	+	–	–	+
3	–	–	+	+	+	+	+
4	–	–	+	+	+	+	–

Таблица 7.2

	1	2	3	4	5	6	7
1	0.5	0.6	0.65	0.5	–	0.7	0.6
2	–	–	0.6	0.7	–	–	0.4
3	–	–	0.7	0.7	0.4	0.55	0.65
4	–	–	0.75	0.6	0.4	0.5	–

Таблица 7.3

	1	2	3	4	5	6	7
1	0.6	0.7	0.4	0.8	–	0.7	0.6
2	–	–	0.5	0.6	–	–	0.5
3	–	–	0.4	0.4	0.4	0.8	0.6
4	–	–	0.6	0.3	0.35	0.6	–

Требуется:

• определить вероятность перехода ситуации в чрезвычайную под воздействием одного определенного из факторов ;

• определить вероятность перехода ситуации в чрезвычайную под воздействием хотя бы одного из заданной совокупности факторов;

• ранжировать по уровню опасности ситуации под воздействием хотя бы одного из заданной совокупности факторов.

Решить задачу при условии , что вероятность события , при котором под воздействием фактора ситуация может перейти в чрезвычайную зависит от полноты и достоверности информированности.Данная зависимость записывается в виде:

Дополнительно задана матрица достоверности информированности .

Таблица 7.4

	1	2	3	4	5	6	7
1	0.7	0.8	0.4	0.7	–	0.7	0.7
2	–	–	0.3	0.8	–	–	0.8
3	–	–	0.3	0.8	0.4	0.6	0.6
4	–	–	0.5	0.7	0.3	0.7	–

Матрицы – , определяются экспертами и задают предварительные оценки соответствующих показателей.

Решение

Под воздействием множества неконтролируемых факторов риска ситуация может перейти в чрезвычайную. Переход зависит от определенного набора воздействующих факторов:

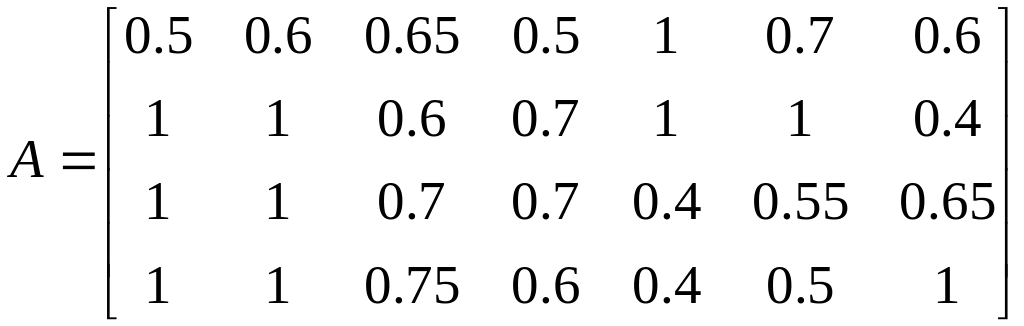
По условию задачи заданы матрицы коэффициентов (в программе это матрица А) и матрицы показателей полноты информированности и достоверности информированности (в программе это матрицы соответственно).

Содержательный смысл коэффициентов может быть определен исходя из следующих рассуждений. Предположим, что уровень информированности ЛПР=1, и тем не менее, существует ненулевая вероятность перехода ситуации в чрезвычайную. Обозначим ее .

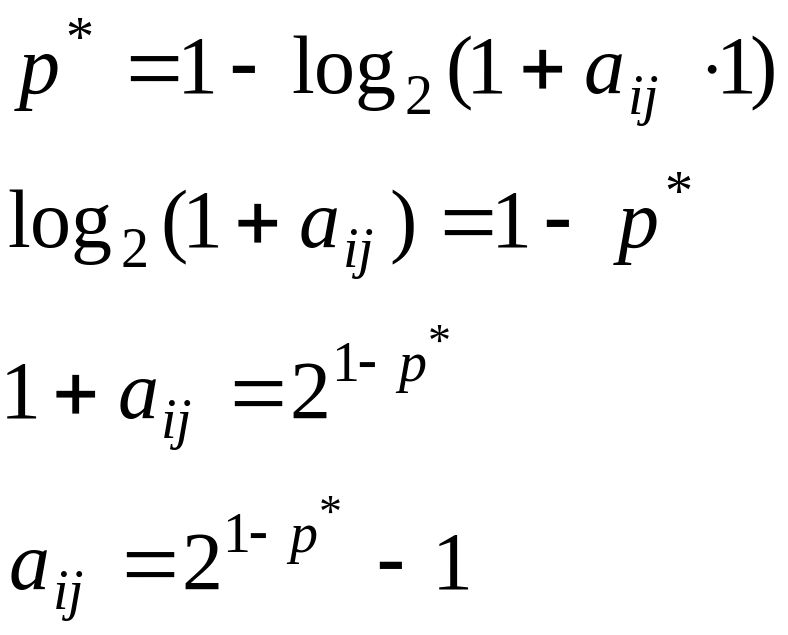
Таким образом, коэффициенты нормированы, и могут быть вычислены при наличии предварительных оценок и предположений ЛПР о возможной вероятности возникновения чрезвычайной ситуации даже в случае полной информированности. Отметим, что идеальным является случай , в таких обстоятельствах при полной информированности о некотором факторе риска можно гарантировать то, что ситуация не станет чрезвычайной. В другом крайнем случае – , имеет место факт, что при любом уровне информированности о влиянии фактора риска на ситуацию, ситуация перейдет в чрезвычайную (вероятность=1).

Определим вероятность перехода ситуации в чрезвычайную под воздействием одного определенного фактора риска . Для этого воспользуемся формулой:

Данная матрица задает вероятность перехода критической ситуации в чрезвычайную под воздействием одного из факторов риска. Как видно из матрицы, вероятности перехода достаточно большие (>0.8).

Определим вероятность перехода ситуации в чрезвычайную под воздействием хотя бы одного из заданной совокупности факторов. Данная вероятность задается зависимостью: 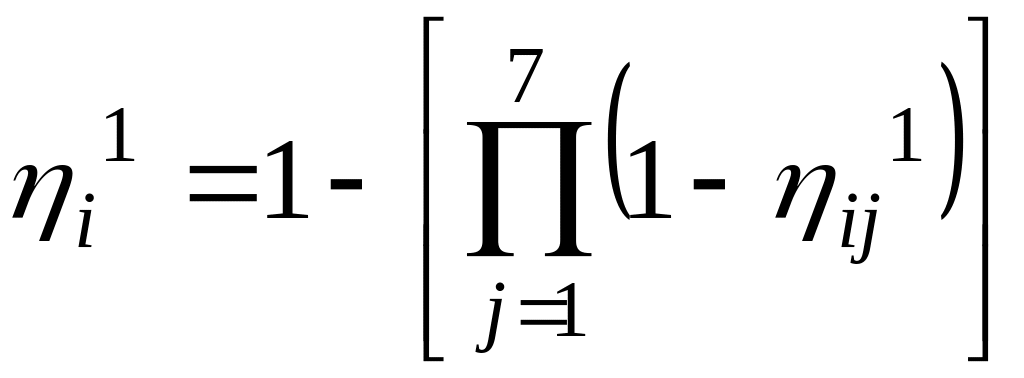, (в программе это вектор )

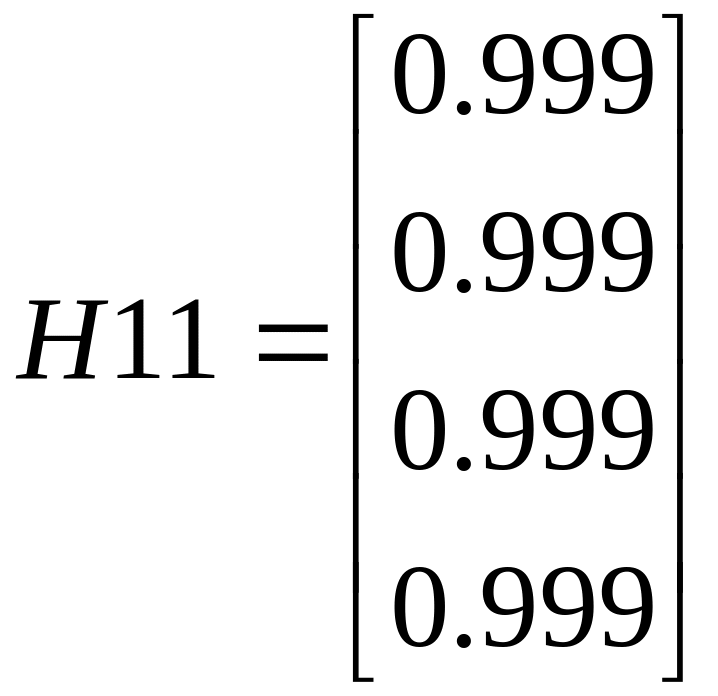
Ранжируем по уровню опасности ситуации складывающиеся под воздействием одного из заданной совокупности факторов.

Таблица 7.5

Сокращение	Качественная характеристика степени риска	Количественное описание
ч.н.	чрезвычайно низкий	0.0–0.1
о.н.	очень низкий	0.1–0.25
н.	низкий	0.25–0.4
с.	средний	0.4–0.6
в.	высокий	0.6–0.75
о.в.	очень высокий	0.75–0.9
ч.в.	чрезвычайно высокий	0.9–1.0

Таблица 7.6

	о.в.	о.в.	о.в.	о.в.	–	о.в.	о.в.
	–	–	о.в.	о.в.	–	–	ч.в.
	–	–	о.в.	о.в.	ч.в.	о.в.	о.в.
	–	–	о.в.	ч.в.	ч.в.	о.в.	–

Определим вероятность перехода ситуации в чрезвычайную под воздействием одного определенного фактора риска с учетом полноты и достоверности информированности. Воспользуемся формулой:

где – коэффициент, который вычисляется при наличии предварительных оценок и предположений ЛПР о возможной вероятности возникновения чрезвычайной ситуации даже в случае , когда уровень достоверности равен 1. Пусть – ненулевая вероятность перехода критической ситуации в чрезвычайную, тогда :

В данной работе и в вариантах для выполнения лабораторной работы принимается =10. При выполнении задания (свой пример) данный коэффициент необходимо вычислить.

Матрица для имеет вид:

Определим вероятность перехода ситуации в чрезвычайную под воздействием хотя бы одного из заданных совокупности факторов с учетом полноты и достоверности информированности .Данная вероятность задается зависимостью :

В программе это вектор Н22

Ранжируем по уровню опасности ситуации, складывающиеся под воздействием одного из заданной совокупности факторов при условии, что учитываются полнота и достоверность информированности.

Таблица 7.7

	с.	н.	о.в.	с.	–	н.	с.
	–	–	в.	н.	–	–	с.
	–	–	в.	с.	о.в.	с.	о.в.
	–	–	с.	в.	о.в.	с.	–

Задача распознавания ситуации в условиях нечеткости информации в динамике изменения информированности.

При условиях задачи 1 дополнительно известно, что полнота информированности ЛПР возрастает во времени и определяется следующим образом:

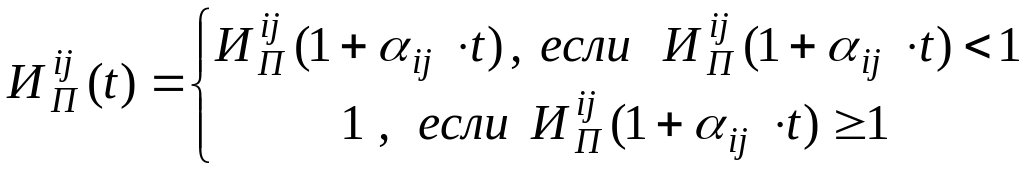
Достоверность информированности возрастает во времени и определяется следующим образом :

Одновременно уменьшается своевременности информированности ЛПР в соответствии с

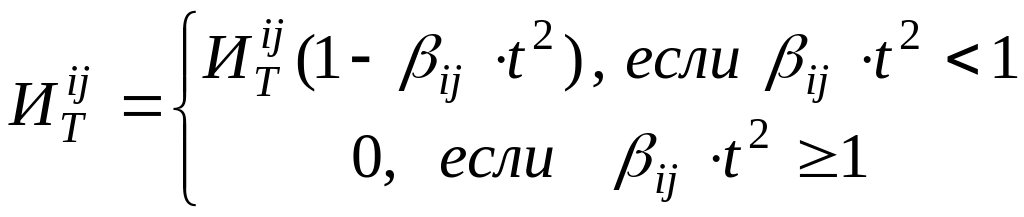
где – своевременность (табл. 7.8), , – коэффициенты связи, влияния и приоритета.

Таблица 7.8

	1	2	3	4	5	6	7
1	0.8	0.8	0.6	0.8	–	0.8	0.9
2	–	–	0.7	0.9	–	–	0.6
3	–	–	0.5	0.8	0.5	0.7	0.75
4	–	–	0.8	0.75	0.55	0.8	–

Коэффициенты задаются зависимостями:

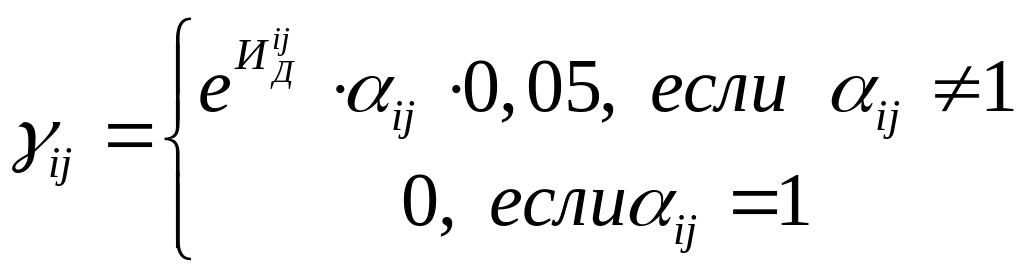
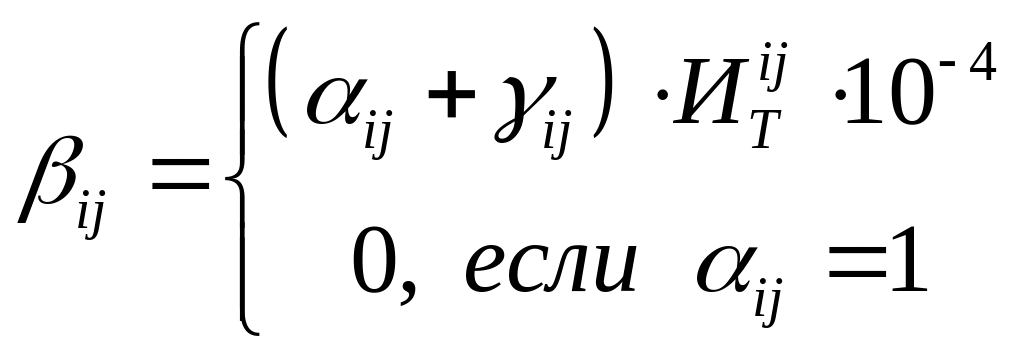
Вероятность перехода ситуации в чрезвычайную под воздействием факторов определяется

.

Требуется определить допустимое время на формирование и реализацию решения, при котором вероятность перехода ситуации в чрезвычайную не будет превышать заданной величины допуска .

Решение

Для того, чтобы найти допустимое время необходимо найти решение неравенства:

,

т.е. , где – соответственно, нижняя и верхняя граница решения неравенства.

Дополнительно задана матрица показателя своевременности информированности (в программе ).

Найдем коэффициенты .

Таблица 7.9

	[0; 30,2]	[0; 33,4]	[0; 36,2]	[0; 32,2]	–	[0; 27,2]	[0; 29,1]
	–	–	[0; 39,4]	[0; 36,3]	–	–	[0; 41,3]
	–	–	[0; 45,5]	[0; 35,4]	[0; 43,9]	[0; 28,2]	[0; 32,1]
	–	–	[0; 31,3]	[0; 35,3]	[0; 30,1]	[0; 33,3]	–

Задача отнесения ситуации к определенному классу критических ситуаций.

Задано три класса критических ситуаций:

• - класс особо опасных ситуаций, для которых общее время формирования и реализации решения (период от начала формирования до реализации)

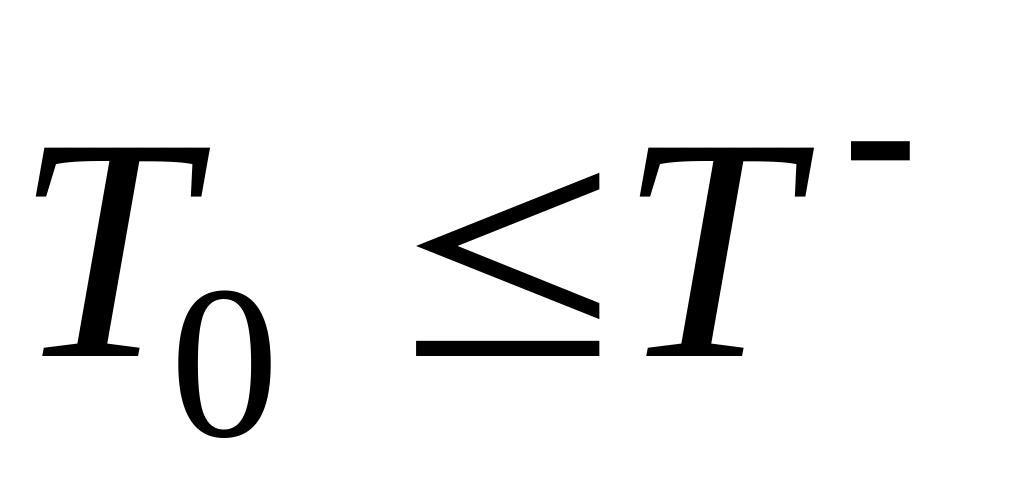
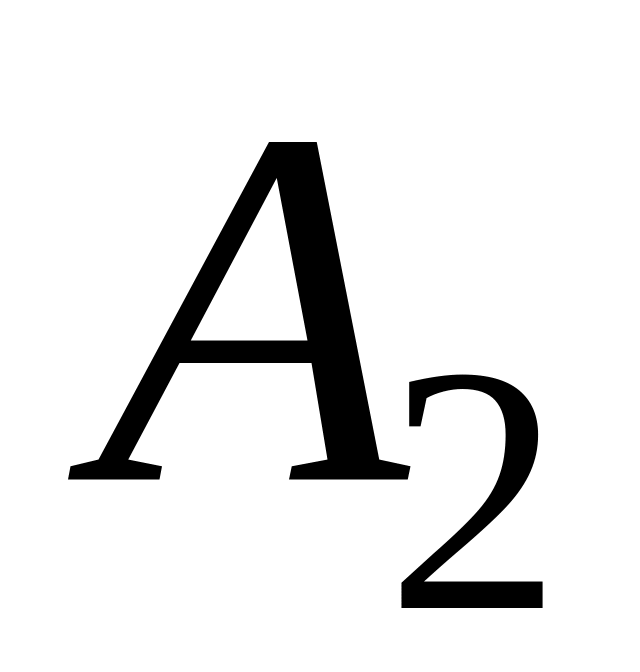• - класс потенциально опасных ситуаций, для которых

• - класс практически неопасных ситуаций

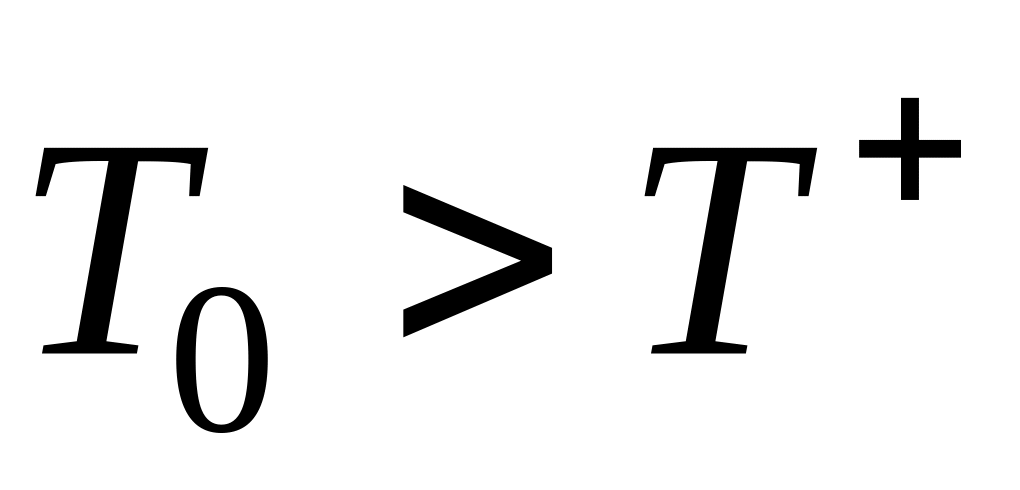
Требуется определить к какому классу относится ситуация ,при заданных границах области.

Ход решения

Найдем допустимый временной интервал на формирование и реализацию решения , при котором вероятность перехода ситуации в чрезвычайную не будет превышать заданной величины допуска для по всем факторам.

Найдем результирующий допустимый временной интервал на формирование и реализацию решения , при котором вероятность перехода ситуации в чрезвычайную не будет превышать заданной величины допуска для как пересечение соответствующих временных интервалов по всем факторам.

Построим функцию принадлежности момента времени допустимому временному интервалу , как , где минимальная величина допуска при которой .

Построим функции принадлежности , , момента времени соответственно классу А₁, А₂ и А₃.

Данный алгоритм повторим для каждой ситуации .

Ход работы

Дано: временные функции частных показателей информированности и таблицы коэффициентов по четырем рисковым ситуациям при семи разнородных факторах риска . Прочерк в таблице – отсутствие влияния данного фактора риска.

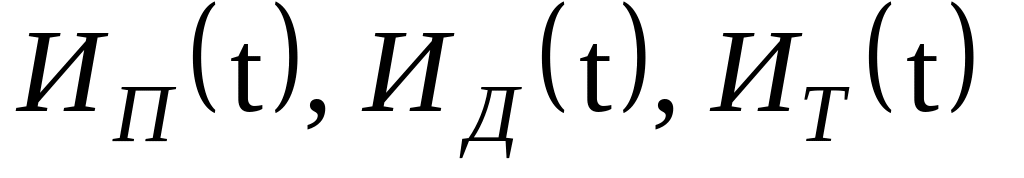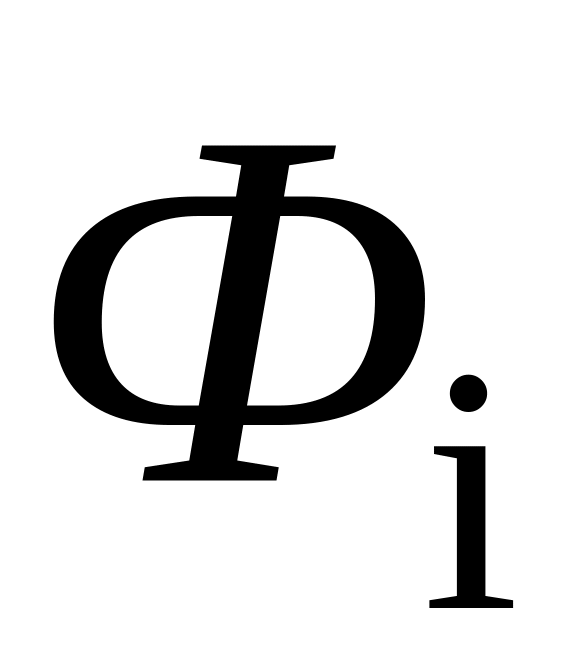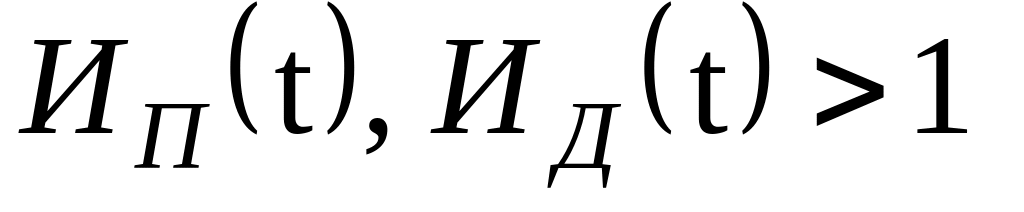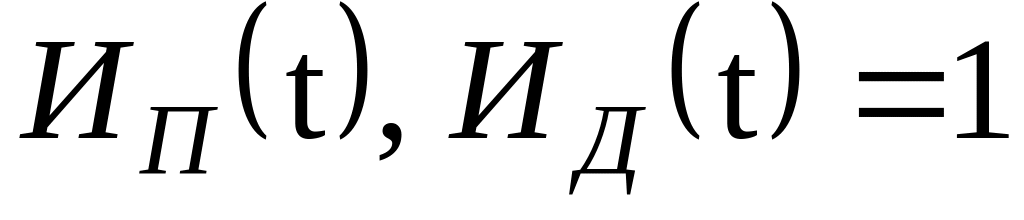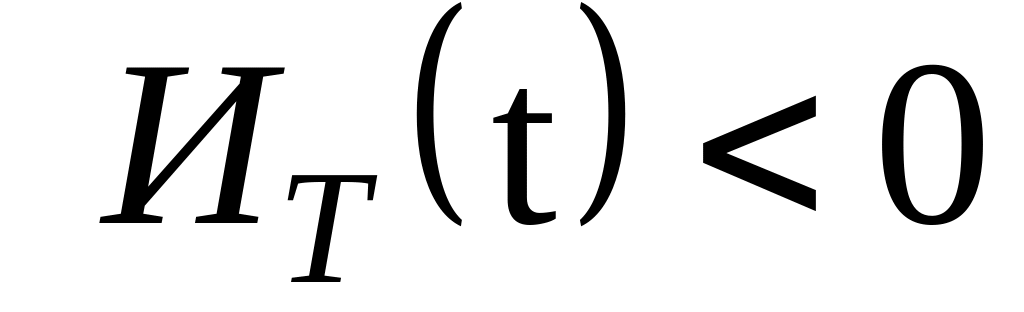• Построить графики в одной координатной плоскости для (указанные в вариантах задания) по каждому фактору риска (i=1,7). Замечание: если частные показатели полноты и достоверности информированности тогда . Если частный показатель своевременности информированности , то .

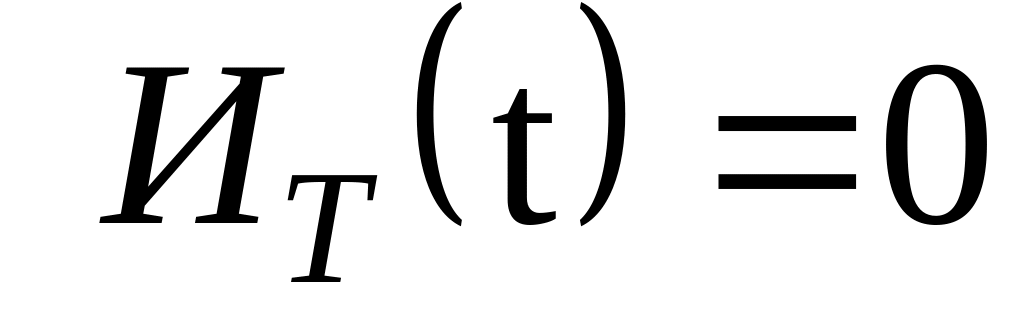• Определить временной интервал рационально достаточный для формирования и реализации решения по частным показателям, если известно, что 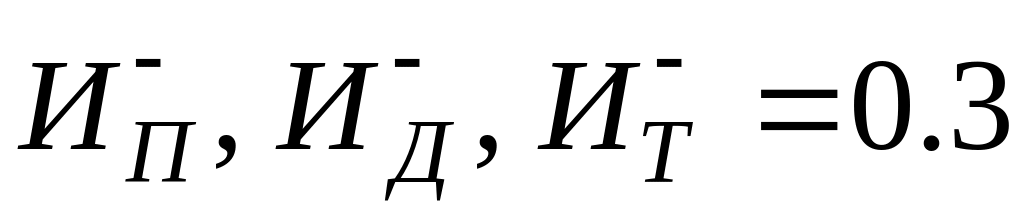и . Сделать выводы.

• Построить графики функций интегрального показателя информированности .

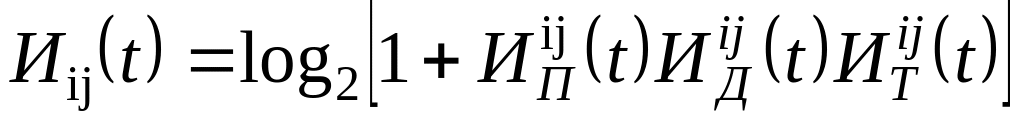• Для заданной ситуации в условиях влияния какого-либо из факторов риска определить допустимое время как 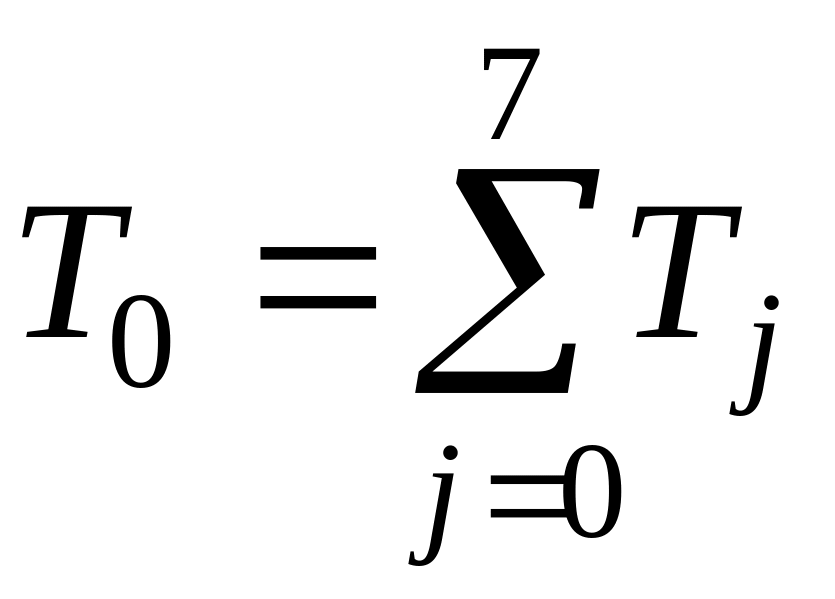, на формирование и реализацию решения. 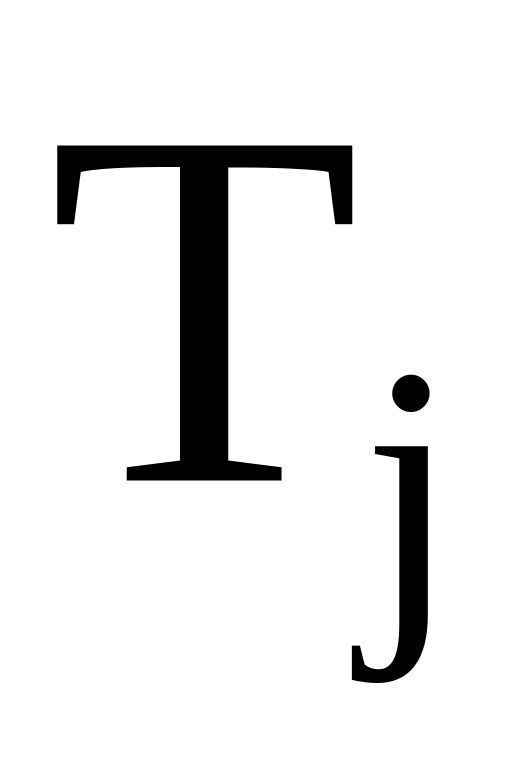определено из условия 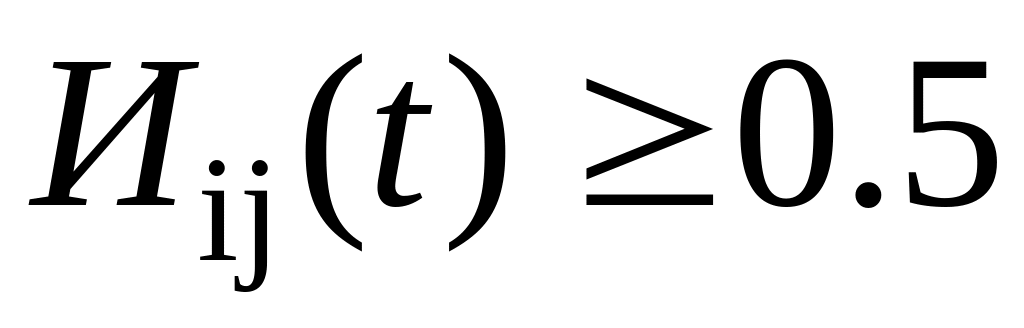. Если 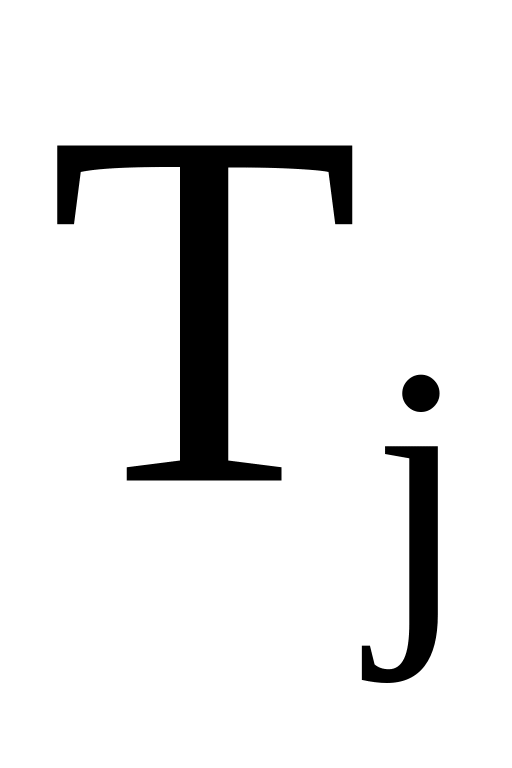пуст, изменить коэффициенты в матрицах, чтобы получить ненулевые решения.

Границы области заданы следующим образом:

	20	25	30	35	40	45	50	55	60	65	70
	1,0	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0

	1	2	3	4	5	6	7	8	9	10	11
	0	0,1	0,3	0,5	0,7	0,8	1,0	0,9	0,7	0,5	0,3

Определить к какому классу относится ситуация . .

Варианты задания к лабораторной работе №7

	1	2	3	4	5	6	7
1	0.3	–	0.45	0.25	–	–	0.45
2	0.2	0.5	–	0.35	–	0.45	–
3	0.4	–	0.6	–	0.2	0.3	–
4	0.5	0.35	–	–	–	0.35	0.55
5	0.1	–	0.2	0.5	0.55	–	–
6	0.25	–	–	–	0.25	0.55	0.1
7	0.35	–	0.5	–	0.45	–	0.2
8	0.45	0.35	–	0.25	0.35	–	–
9	0.2	0.75	0.1	0.2	–	–	–
10	0.3	0.3	0.4	–	–	–	0.45
11	0.1	–	0.75	–	–	0.35	0.25
12	0.5	–	–	0.45	0.35	0.25	–
13	0.6	0.35	0.25	–	–	–	0.55
14	0.25	–	–	–	0.4	0.5	0.6
15	0.55	–	0.55	0.3	0.2	–	–
16	0.65	0.3	–	0.1	–	0.2	–
17	0.5	0.5	–	0.3	–	–	0.2
18	0.4	–	0.55	0.35	–	–	0.35
19	0.3	0.2	–	–	0.55	0.35	–
20	0.2	–	0.5	0.7	–	–	0.25

	1	2	3	4	5	6	7
1	0.4	–	0.4	0.3	–	–	0.25
2	0.4	0.6	–	0.3	–	0.55	–
3	0.5	–	0.35	–	0.7	0.45	–
4	0.5	0.25	–	–	–	0.15	0.35
5	0.25	–	0.35	0.65	0.65	–	–
6	0.1	–	–	–	0.45	0.15	0.55
7	0.3	–	0.2	–	0.55	–	0.45
8	0.25	0.5	–	0.55	0.2	–	–
9	0.4	0.55	0.3	0.45	–	–	–
10	0.4	0.65	0.35	–	–	–	0.15
11	0.3	–	0.65	–	–	0.25	0.35
12	0.35	–	–	0.25	0.3	0.35	–
13	0.55	0.25	0.55	–	–	–	0.45
14	0.65	–	–	–	0.35	0.45	0.5
15	0.1	–	0.45	0.35	0.45	–	–
16	0.35	0.2	–	0.3	–	0.25	–
17	0.25	0.35	–	0.2	–	–	0.4
18	0.2	–	0.35	0.45	–	–	0.3
19	0.45	0.1	–	–	0.15	0.15	–
20	0.35	–	0.25	0.6	–	–	0.15

	1	2	3	4	5	6	7
1	0.35	–	0.7	0.2	–	–	0.5
2	0.45	0.7	–	0.4	–	0.45	–
3	0.55	–	0.6	–	0.4	0.65	–
4	0.4	0.65	–	–	–	0.25	0.55
5	0.35	–	0.5	0.45	0.65	–	–
6	0.25	–	–	–	0.65	0.55	0.45
7	0.1	–	0.25	–	0.75	–	0.35
8	0.65	0.55	–	0.35	0.35	–	–
9	0.35	0.25	0.35	0.55	–	–	–
10	0.45	0.55	0.2	–	–	–	0.55
11	0.45	–	0.3	–	–	0.35	0.65
12	0.65	–	–	0.5	0.45	0.55	–
13	0.35	0.75	0.75	–	–	–	0.55
14	0.55	–	–	–	0.25	0.15	0.45
15	0.35	–	0.55	0.3	0.3	–	–
16	0.65	0.25	–	0.4	–	0.3	–
17	0.55	0.15	–	0.5	–	–	0.35
18	0.25	–	0.45	0.35	–	–	0.25
19	0.35	0.15	–	–	0.2	0.35	–
20	0.55	–	0.35	0.3	–	–	0.1

	1	2	3	4	5	6	7
1	0.1	–	0.1	0.3	–	–	0.15
2	0.2	0.2	–	0.3	–	0.15	–
3	0.3	–	0.25	–	0.1	0.15	–
4	0.45	0.35	–	–	–	0.15	0.25
5	0.5	–	0.55	0.1	0.15	–	–
6	0.6	–	–	–	0.15	0.45	0.65
7	0.75	–	0.6	–	0.35	–	0.25
8	0.55	0.15	–	0.75	0.75	–	–
9	0.45	0.65	0.75	0.25	–	–	–
10	0.35	0.75	0.6	–	–	–	0.15
11	0.25	–	0.15	–	–	0.75	0.35
12	0.6	–	–	0.45	0.25	0.25	–
13	0.55	0.25	0.45	–	–	–	0.15
14	0.5	–	–	–	0.65	0.75	0.75
15	0.4	–	0.15	0.75	0.6	–	–
16	0.35	0.15	–	0.3	–	0.65	–
17	0.25	0.45	–	0.25	–	–	0.25
18	0.15	–	0.35	0.75	–	–	0.15
19	0.55	0.55	–	–	0.5	0.1	–
20	0.45	–	0.75	0.55	–	–	0.4

Для нечетных вариантов	Для четных вариантов

Пример выполнения лабораторной работы.

Матрицы:

коэффициентов

полноты информированности Ип

достоверности информированности Ид

своевременности информированности Ит

1. Определим параметры 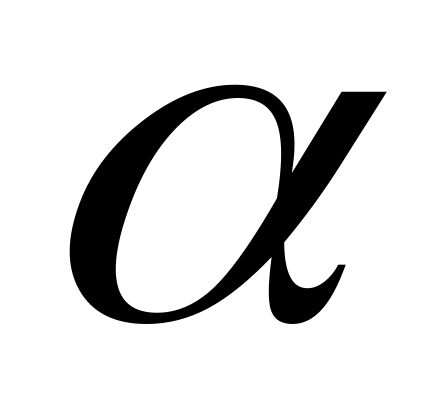, 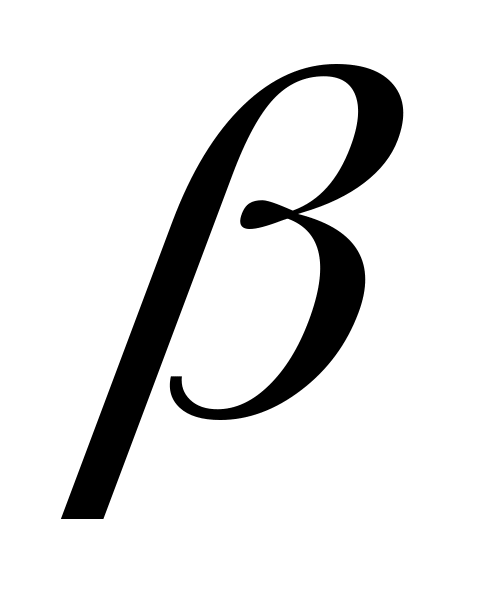и

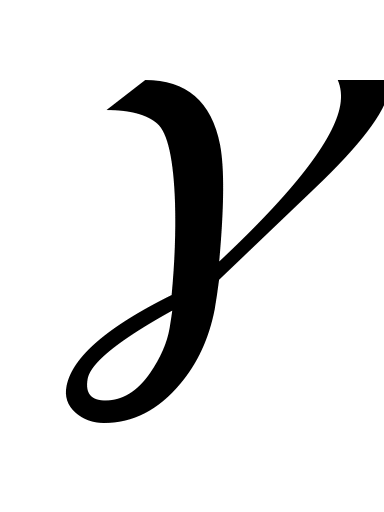
Полнота информированности во времени

Достоверность информированности во времени

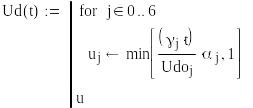
Своевременность информированности во времени

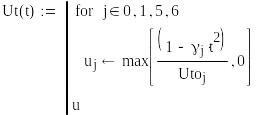
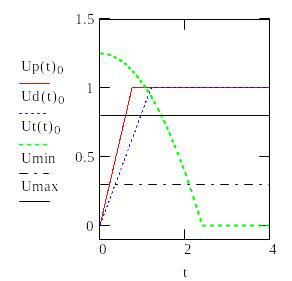
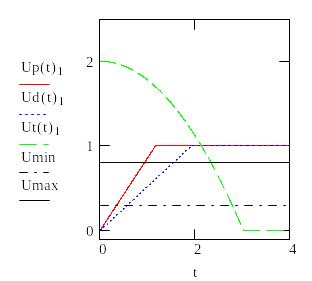
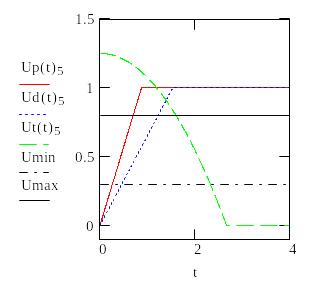
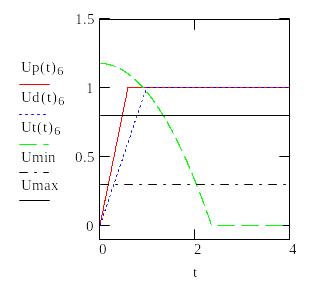
Графики для факторов риска

S1		S2
S6		S7

Факторы риска Ф3, Ф4, Ф5 не влияют на возникновение рисковой ситуации согласно заданию

2. Определим интегральный показатель информированности

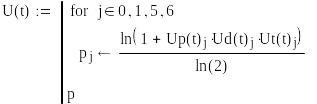
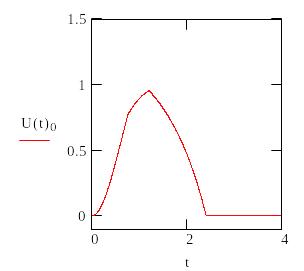
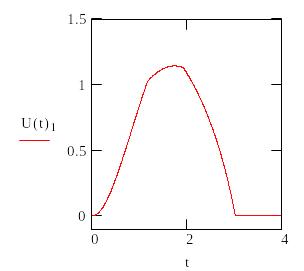
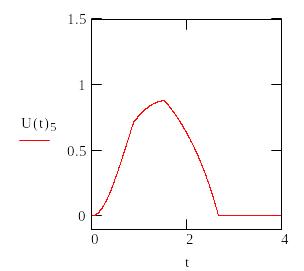
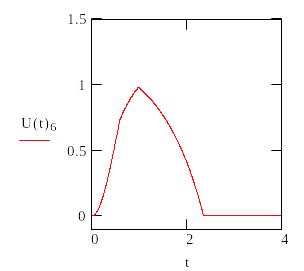
3. Определим допустимое время To из условий U(t)>0.5

Для Ф1	Для Ф2	Для Ф5	Для Ф6

Время на формирование решения То должно лежать в диапазоне 0.4<To<2.7 чтобы не допустить переход ни к одной чрезвычайной ситуации с вероятностью, большей 0.5

4. Определим к какому классу относится ситуация S

Границы области заданы нечеткими множествами

Построим графики функций принадлежности

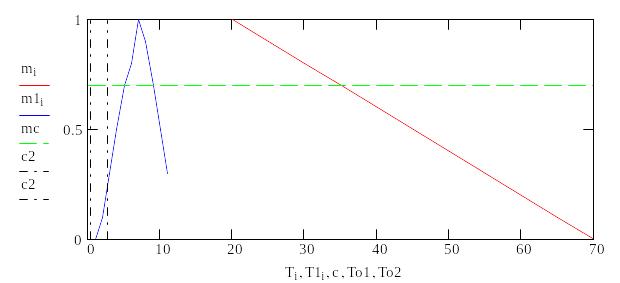
Так как время формирования и реализации решения То лежит в диапазоне 0.4<To<2.7 и оказывается менше нижней границы T– при 0.7, то ситуация S4 относится к классу А1 – особо опасных ситуаций.