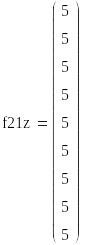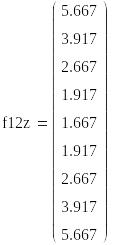Лабораторная работа 5 Принятие решений в условиях неопределенности. Критерии Лапласа, Вальда, Гурвица, Сэвиджа

Цель работы: научиться применять критерии принятия решений в условиях неопределенности и выбирать наилучший критерий в соответствии со спецификой конкретной задачи.

Теоретические сведения

Одним из определяющих факторов в задачах принятия решений в условиях неопределенности является внешняя среда (или природа), которая может находиться в одном из к состояний , неизвестных лицу, принимающему решение (ЛПР) [4–6].

Тогда математическую модель задачи принятия решений в условиях неопределенности можно сформулировать следующим образом.

Имеется некоторая матрица размерностью . Элемент этой матрицы uij можно рассматривать как полезность результата при использовании стратегии :

, .

(5.1)

В зависимости от состояния природы S_k результат у_j достигается с вероятностью Р(у_j |x_i, S_k). Кроме того, ЛПР неизвестны априорные вероятности P(S_k). Лицо, принимающее решение, может высказывать определенные гипотезы, относительно состояния природы. Его предположения о возможном состоянии природы называют субъективными вероятностями:

, .

(5.2)

Если бы величина P(S_k) была известна лицу, принимающему решение, то мы бы имели задачу принятия решений в условиях риска. В этом случае правило принятия решений определяется следующим образом:

(5.3)

На самом деле текущее состояние природы неизвестно ЛПР, неизвестно также распределение вероятностей . Как выбрать при этом оптимальную стратегию? Существует несколько критериев для выбора оптимальной стратегии.

Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что природа (внешняя среда) находится в самом невыгодном для наблюдателя состоянии. По данному критерию правило принятия решений имеет следующий вид:

(5.4)

где

.

(5.5)

По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния природы.

Критерий Гурвица основан на следующих двух предположениях: природа может находиться в самом невыгодном состоянии с вероятностью 1–α и в самом выгодном – с вероятностью α, где α – коэффициент доверия.

Тогда правило принятия решений записывается так:

, 0≤α≤1.

(5.6)

Если α=0 , то получим критерий Вальда. Если α=1, то имеем правило вида , – которое имеет название стратегии оптимиста, который верит в свою удачу.

Критерий Лапласа. Если состояния природы (среды) неизвестны, то все они считаются равновероятными:

(5.7)

Критерий Сэвиджа (критерий минимизации сожалений). Сожаление – это величина, равная изменению полезности решения (результата) при данном текущем состоянии среды относительно наилучшего возможного состояния (для данного решения). Чтобы определить сожаление, выполняют следующие процедуры.

Вычисляют матрицу , где , , . В каждом столбце этой матрицы находят максимальный элемент:

, .

(5.8)

Его вычитают от всех элементов столбца. Затем строят матрицу сожалений: где

Правило выбора оптимальной стратегии в соответствии с критерием Сэвиджа записывается так:

(5.9)

Ход работы

Для заданных целевых функций двух игроков и диапазонов изменения переменных определить:

Гарантированный результат каждого игрока, используя следующие критерии:Вальда – ;

Лапласа – ;

Сэвиджа – ;

Гурвица

при значения переменных :

• табличным методом (шаги сетки указаны);

• аналитическим методом (найти нужные экстремумы функций, исследуя частные производные в указанных диапазонах переменных).

Второй и третий пункты выполнить для значений, полученных по критерию Вальда.

Найти область Х (точки на плоскости )из условия и , где значения просчитаны табличным способом так, как показано в предыдущем пункте.

Определить оптимальные значения : при которых ,где (при этом перебор делать по узлам сетки области Х, которая найдена в п.2).

Примечание. Варианты заданий следует согласовать с преподавателем.

Варианты заданий к лабораторной работе №5

1			0.5		–2	2
			0.5		–2	2
2			0.2		–1	1
			0.2		–1	1
3			0.5		–2	2
			0.5		–2	2
4			0.5		–3	2
			0.5		–3	2
5			0.3		–1.5	1.5
			0.3		–1.5	1.5
6			0.2		–1	1
			0.2		–1	1
7			0.5		–2	2
			0.5		–2	2
8			0.2		–1	1
			0.2		–1	1
9			0.5		–2	2
			0.5		–2	2
10			1		–4	4
			1		–4	4
11			0.3		–1.5	1.5
			0.3		–1.5	1.5
12			0.2		–1	1
			0.2		–1	1
13			0.5		–2	2
			0.5		–2	2
14			0.2		–1	1
			0.2		–1	1
15			0.5		–2	2
			0.5		–2	2

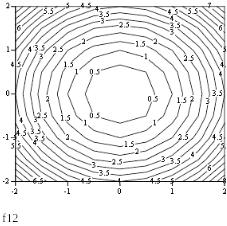
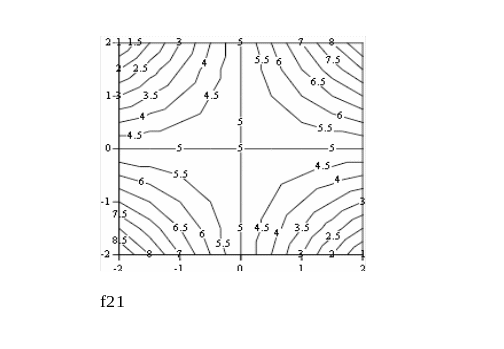
Пример выполнения лабораторной работы

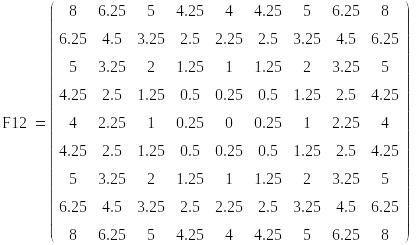
Табличный метод

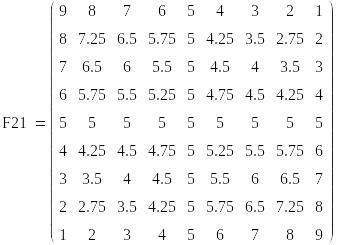
Определим гарантированный результат по критерию Вальда

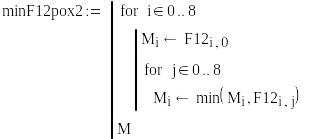
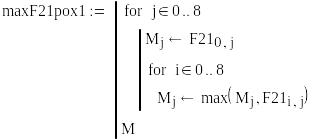
Определим гарантированный результат по критерию Лапласа

Гарантированный результат по критериям

Лапласа Вальда

для первого игрока

для второго игрока

Примечание: Результат по критериям Гурвица и Сэвиджа получить самостоятельно.

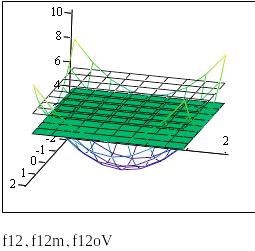
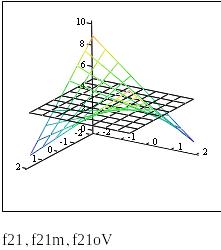
Множество Парето определяется системой неравенств

f12>f12o f21>f21o по табличным значениям

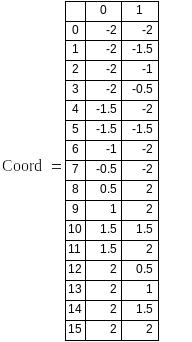
Координаты допустимых точек области Парето на плоскости х1,х2

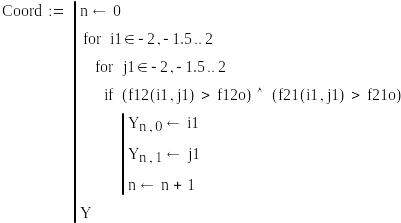
Определим оптимальные значения х1о и х2о перебором по допустимым узлам сетки

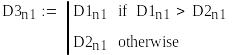
Оптимальные значения х1о и х2о соответственно:

–2, –0.5

–0.5, –2

0.5, 2

2, 0.5

Аналитический метод анализа экстремумов функций

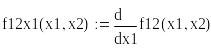
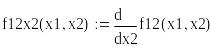
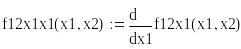
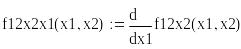
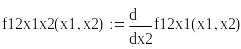
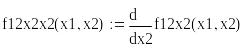
Критическая точка х1=0, х2=0

Проверим наличие экстремума

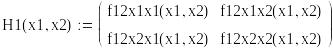
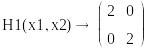
В критической точке – минимум

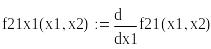
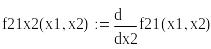
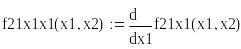
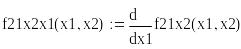
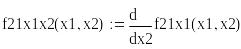
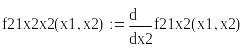
Критическая точка х1=0, х2=0

Проверим наличие экстремума

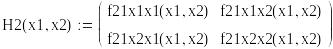
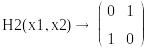
Критическая точка – точка перегиба (седловая)