Лабораторная работа 4 Раскрытие неопределенностей в задачах системного анализа

Цель работы: научиться находить область Парето и определять условия рационального компромисса для заданных целевых функций и ограничений.

Теоретические сведения

Одним из методов раскрытия неопределенностей в задачах системного анализа является метод, предложенный Парето: попытаться сократить множество исходных вариантов решений путем исключения из анализа таких вариантов, которые заведомо являются непригодными [2–7]. Реализация этой идеи осуществляется следующим образом. Положим, что сделан некоторый выбор вектора , обозначим его значение . Делаем теперь некоторый другой выбор такой, что для всех целевых функций

(4.1)

Все векторы со значением , для которых выполняется условие (4.1), следует исключить из данного анализа. Подвергать неформальному анализу, сопоставлять между собой следует те векторы , для которых не существует такого значения (хотя бы для одной из заданных целевых функций) для которого выполняется неравенство (4.1).

Множество всех значений для которых невозможно подобрать из условия (4.1), называется множеством Парето, а вектор называется неулучшаемым вектором результатов (вектор Парето).

Рассмотрим подход к нахождению множества Парето.

Пусть известен вектор целевых функций , заданных на множестве , в виде

,

Найдем такое множество граничных значений , которое делит исходное множество на два множества: множество и множество . Это множество должно удовлетворять условию

(4.2)

Множество состоит из таких значений , для которых для всех выполняется условие . Множество определяется соотношением

(4.3)

Множество состоит из таких для которых хотя бы для одной функции выполняется условие . Множество описывается следующим соотношением:

.

Таким образом, вектор является вектором неулучшаемых результатов, а множество , удовлетворяющее условию (4.3), является множеством Парето.

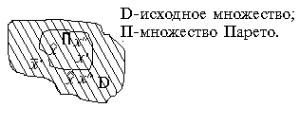
Рис. 4.1. Иллюстрация подхода к нахождению множества Парето

В силу условия (4.4) множество является границей, которая выделяет множество Парето из множества . В соответствии с (4.2) множество является подмножеством исходного множества , из которого выделено множество Парето (рис.4.1). Поэтому все варианты решений, которые принадлежат , исключаются из рассмотрения.

Пример. Пусть требуется выделить множество Парето в области

(рис. 4.2). Разобьем заданное множество на три подмножества. Область – область от 0 до , где – значение , при котором достигает максимума

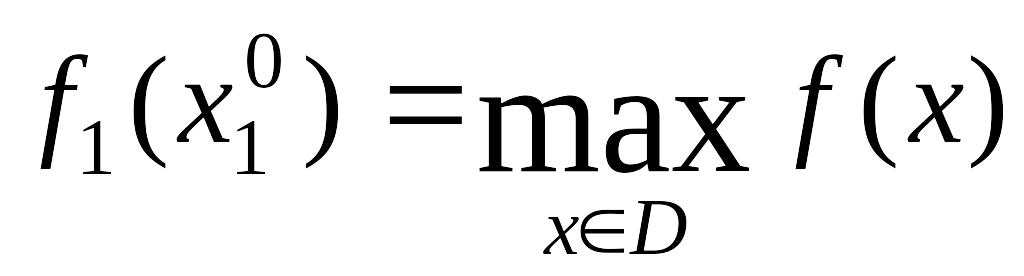
, x[0, ).

Область – область от до , где – такое значение , при котором достигает максимума

, .

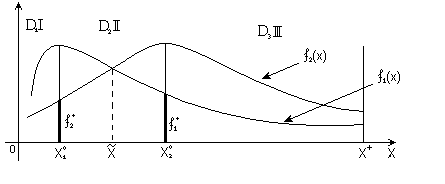
Рис. 4.2. Выделение множества Парето

Область – область от до . Сравним области и . Для них имеем , т.е. значения функции для любого меньше, чем значения для любого . Для имеем , то есть в определенном интервале области значения соизмеримы с ее значениями в определенном интервале области . Следовательно, область заведомо уступает области в смысле целевой функции . Аналогично, для области имеем значение функции для любого меньше, чем значение для любого . Но для имеем , то есть значения соизмеримы в определенном интервале области с ее значениями в определенном интервале области , следовательно, область заведомо уступает области в смысле целевой функции . Таким образом, из области необходимо исключить области и , поскольку в них не выполняется условие (4.1). Область в соответствии с (4.1) является множеством Парето. Для данной области выполняются ограничения:

; .

В теории принятия решений существует принцип, называемый “принципом Парето”, который утверждает, что рациональное решение многокритериальной задачи или рациональный компромисс в многоцелевой задаче находится среди , принадлежащих множеству Парето. Но принцип Парето не позволяет выделить единственное решение. Он позволяет только сузить множество возможных альтернативных решений. В рассматриваемом примере рациональное решение необходимо искать в области .

Возможны различные варианты раскрытия неопределенностей целей на основе приведения многоцелевой задачи к стандартной однокритериальной.

Вариант 1. Введем для каждого значения функцию,

(4.4)

и будем определять такие значения , которые соответствуют условию . Здесь – допустимая многомерная область изменения вектора , заданная, например, с помощью конструктивных или технологических ограничений. При такой постановке задачи гарантируется, что в наихудшем случае, который соответствует , обеспечивается максимальное значение . Такая задача обеспечения является максиминной задачей оптимизации.

Вариант 2. Введем для каждого значения функцию

(4.5)

и будем определять такое значение , при котором функция имеет минимальное значение

(4.6)

При данной постановке задачи гарантируется, что ее решение в наихудшем случае, который соответствует максимуму возможного отклонения , будет обеспечено минимальное значение . Такая задача обеспечения является минимаксной задачей оптимизации.

Отличие вариантов 1 и 2 состоит в том, что они относятся к разным условиям оптимальности. Вариант 1 обеспечивает максимально возможное отклонение среди всех от их заданных значений , поскольку такое отклонение обеспечивается для наихудшего случая, который характеризуется соотношением

(4.7)

Вариант 2 относится к обратной задаче – задаче обеспечения возможного минимального отклонения всех от заданных значений . Такое отклонение достигается для наихудшего случая при условии

(4.8)

Ход работы

При заданных целевых функциях и пороговых значениях определить множество Х, на котором выполняются неравенства , и построить на одном графике зависимости

По найденному интервалу определить область Парето.

Сузить область Парето используя принципы и . Построить на одном графике зависимости и .

При решении уравнений все вычисления провести с точностью до 0.01, шаг сетки брать равным 0.1.

Варианты заданий к лабораторной работе №4

№					границы
1			4	1	[0,4]
2			4	1	[–2,3]
3			1	3	[2,6]
4			1	3	[0,5]
5			1	–2	[–2,2]
6			2	–2	[0,5]
7			10	15	[4,7]
8			2	4	[0,5]
9			14	17	[6,10]
10			4	6	[0,3]
11			2	3	[0,5]
12			2	5	[–6,–2]
13			1	3	[0,4]
14			60	56	[2,9]