Лабораторная работа 3 Точечная аппроксимация функции алгебраическими многочленами методом наименьших квадратов

Цель работы: приобретение практических навыков в нахождении методом наименьших квадратов коэффициентов линейной регрессии и коэффициентов квадратичного аппроксимирующего многочлена для заданных функций.

Теоретические сведения

Если значения функции измерены в результате эксперимента со случайными погрешностями, то проводить интерполяцию нецелесообразно. В таких случаях разумнее применять среднеквадратические приближения, так как они сглаживают отдельные локальные ошибки наблюдения и лучше представляют реальную функциональную зависимость. Построение такого приближения называют сглаживанием экспериментальных данных [1, 2].

Наиболее эффективным методом построения наилучшего среднеквадратического приближения является метод наименьших квадратов.

Пусть функция f(x) задана значениями, которые могут содержать на дискретном или случайном множестве . Выберем систему линейно независимых на множестве функций рассмотрим их всевозможные линейные комбинации:

(3.1)

Будем аппроксимировать функцию обобщенным полиномом (x). По принципу наименьших квадратов параметры аппроксимирующего обобщенного полинома (x) определяется из условия, чтобы квадрат взвешенного квадратичного отклонения функции и (x) на множестве был наименьшим:

(3.2)

Многочлен (x), минимизирующий , называется многочленом наилучшего среднего квадратичного приближения функции , а метод его отыскания – методом наименьших квадратов.

Для определения минимума функции (с₀, с₁, … , с_n) приравниваем к нулю ее частные производные по неизвестным параметрам

(3.3)

Получим систему линейных алгебраических уравнений в развернутом виде

(3.4)

Ее называют нормальной системой метода наименьших квадратов. Определитель системы есть определитель Грамма и в случае линейно независимых функций _i(x), (i= 0,1,2…n) отличен от нуля, т.е. коэффициенты с_i определяются однозначно.

В приложениях метода наименьших квадратов наиболее часто полагают

(3.5)

т.е в качестве приближающей функции берется многочлен

(3.6)

Степень многочлена обычно выбирается значительно меньше числа наблюдений

Для данного частного случая полиномиальной аппроксимации коэффициенты и правые части нормальной системы метода наименьших квадратов определяются по формулам

(3.7)

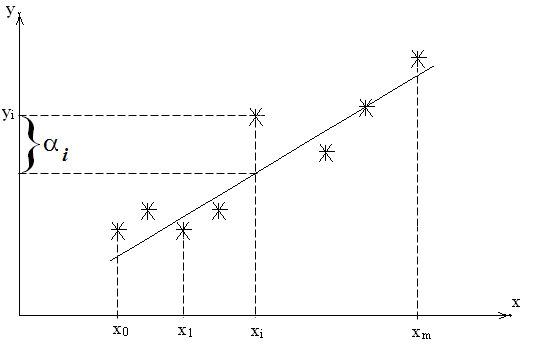
Рис. 3.1. Пример построения линейной регрессии

Если опытные данные при их изображении на графике выстраиваются почти по прямой (рис. 3.1), то сглаживание удобно проводить по прямой, называемой линией регрессии (n = 1)

(3.8)

Параметры ее определяются из системы

(3.9)

Здесь (m +1) – число узлов аппроксимации

При (n = 2) параметры квадратичной аппроксимирующей функции

(3.10)

определяются из системы

(3.11)

Полученные системы линейных алгебраических уравнений можно решить, например, методом Гаусса-Жордана.

Погрешность аппроксимации линейным и квадратичным многочленом определяется по формулам:

,

(3.12)

Ход работы

Для функции, заданной таблично, определить:

• Уравнение линейной регрессии .

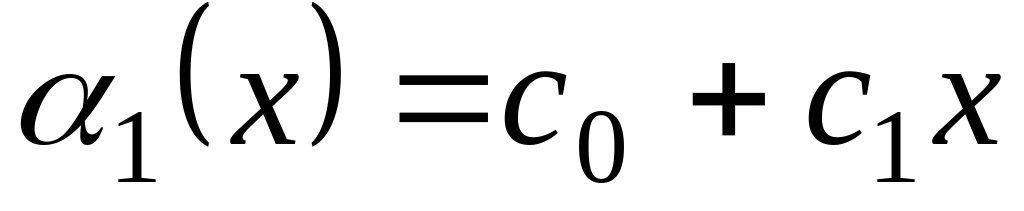• Уравнение квадратичного аппроксимирующего полинома .

• Погрешность аппроксимации линейным и квадратичным многочленом.

• Построить на одном графике функции .

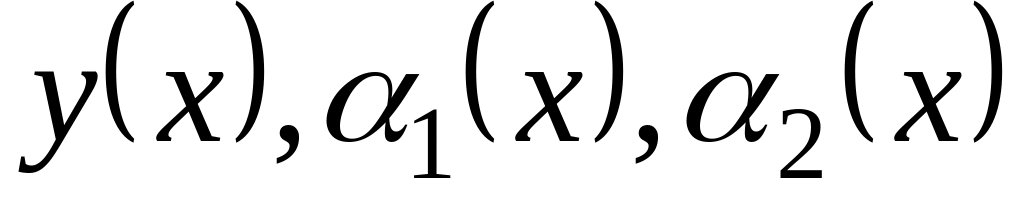Варианты заданий к лабораторной работе №3

	1	2	3	4	5	6	7	8	9	10	11	12
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1
№вар
1	1,21	2,85	3,95	4,41	5,45	6,22	4,88	3,98	3,46	2,33	1,96	1,39
2	2,78	3,67	3,87	4,67	6,91	7,35	6,56	4,78	5,22	3,71	3,23	3,02
3	6,43	5,99	5,55	5,12	4,87	4,56	4,08	4,65	5,89	6,78	7,03	7,45
4	1,27	2,25	3,85	4,45	5,95	6,12	4,33	3,78	3,76	2,53	1,46	1,19
5	2,18	3,57	3,97	4,44	6,96	7,75	6,99	5,66	5,72	3,36	3,13	2,02
6	7,43	6,99	6,55	5,88	4,09	4,02	3,08	4,25	5,19	6,58	7,55	7,98
7	4,48	5,37	6,97	6,64	8,96	9,25	8,59	7,16	7,42	5,76	5,43	4,82
8	3,38	3,63	4,17	4,65	6,51	8,65	7,96	5,78	5,22	3,61	3,83	3,62
9	5,43	5,84	6,78	6,99	7,67	8,75	7,98	6,94	6,67	5,94	5,56	4,78
10	1,42	2,96	3,99	4,62	5,26	6,45	4,97	3,67	3,23	2,67	1,96	1,56
11	9,18	8,57	7,57	7,49	6,95	5,75	6,99	7,66	7,72	8,36	9,13	9,82
12	0,78	1,84	2,94	3,49	4,96	5,66	6,79	5,33	4,68	3,66	2,76	1,69
13	8,67	8,22	7,45	6,48	5,87	4,53	4,59	5,83	6,73	7,59	8,59	9,34
14	0,44	1,56	2,34	3,67	4,24	5,17	6,45	5,03	4,58	3,47	2,16	1,20
15	2,63	3,97	4,16	4,84	6,76	7,17	6,89	5,36	5,55	4,36	3,55	2,67
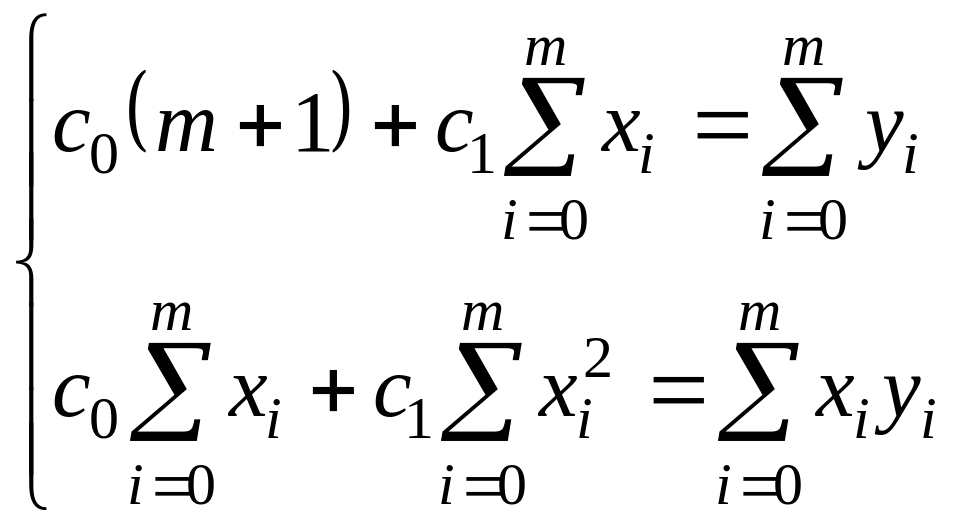
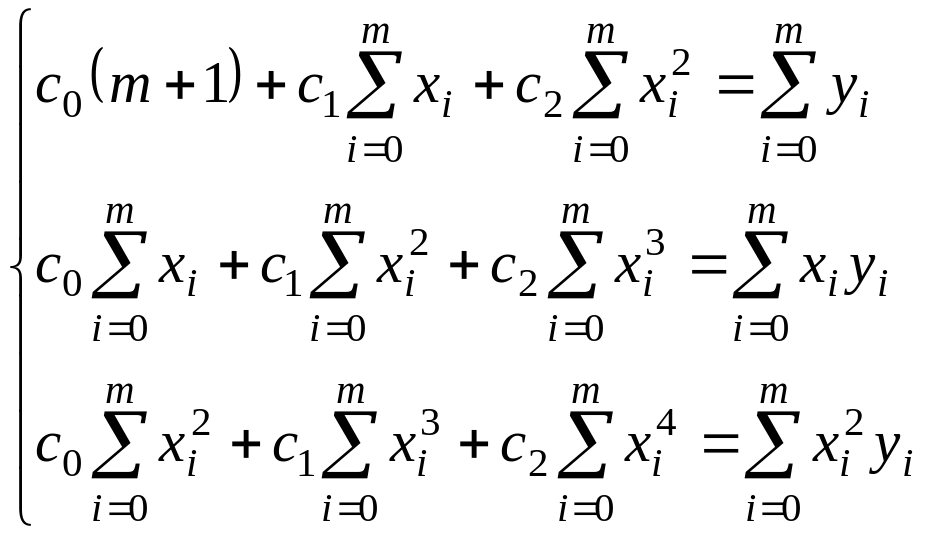