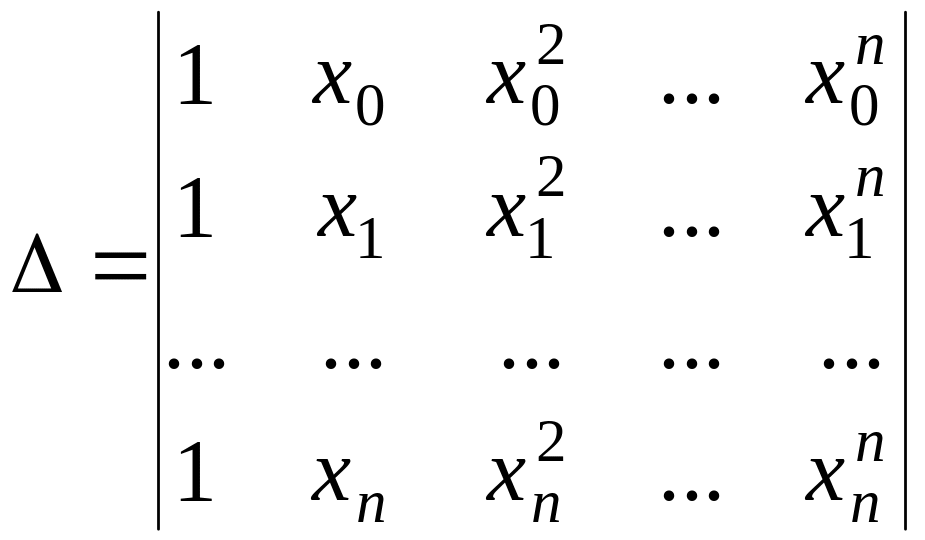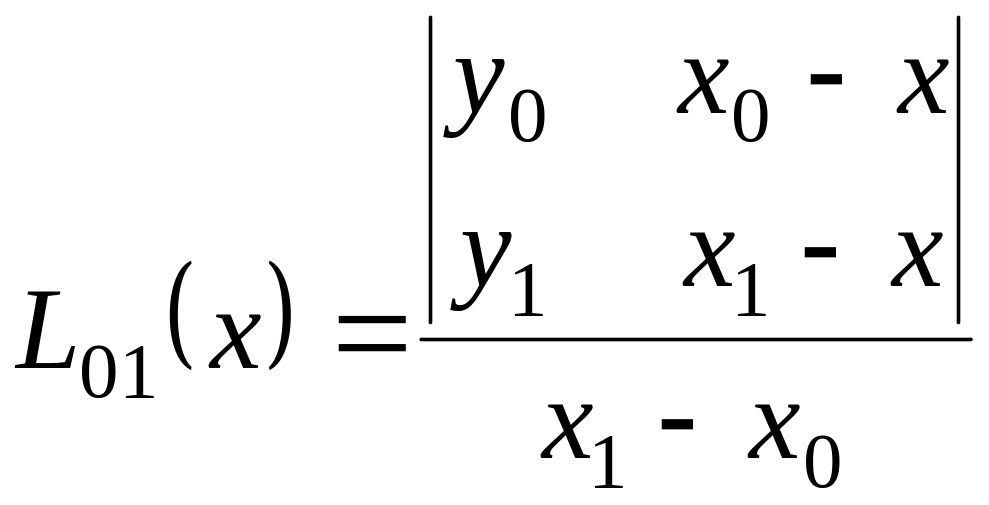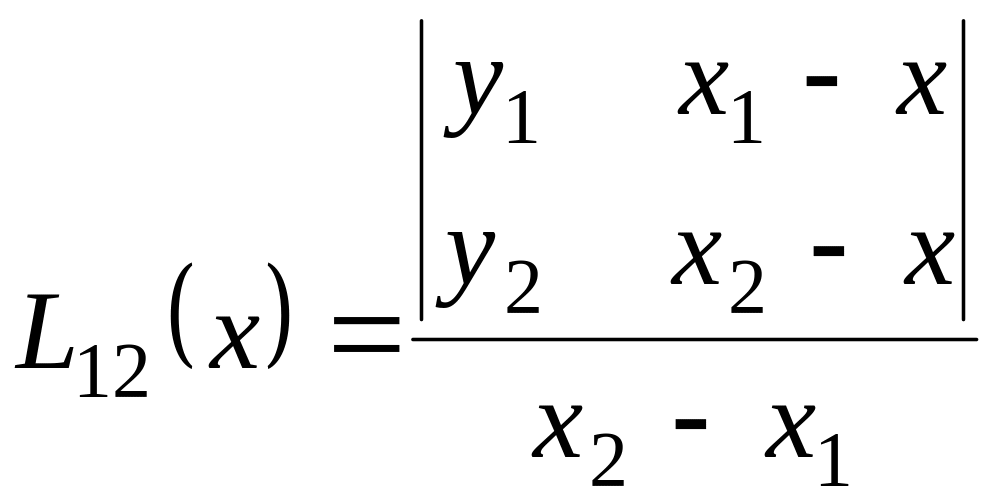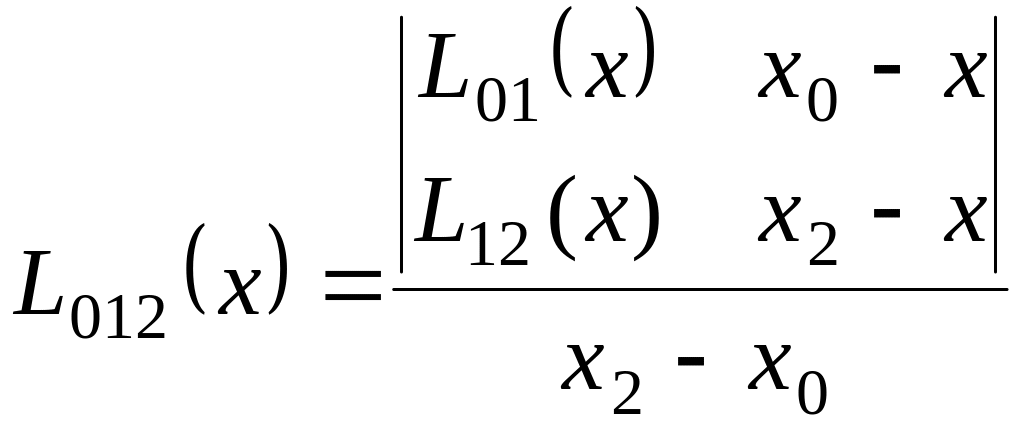Лабораторная работа 2 Аппроксимация функции, заданной таблицей, алгебраическими полиномами

Цель работы: Приобретение практических навыков в аппроксимации функции, заданной таблицей, алгебраическими полиномами.

Теоретические сведения

Задача приближения (аппроксимации) заключается в замене функциональной зависимости, заданной на множестве в виде таблицы, графика, формулы или в неявном виде, более простой приближающей функцией [1, 14].

Если X состоит из дискретного множества точек x₀,x₁…x_m, то приближение называется точечным, а если это отрезок [a;b], то приближение называется интегральным.

Пусть на отрезке [x₀;x_n] заданы точки x₀,x₁…x_n (узлы интерполяции) и известны значения функции y=f(x) в этих точках: y₀=f(x₀), y₁=f(x₁),…, y_n=f(x_n). Требуется построить функцию (х), совпадающую в узлах интерполяции со значениями функции f(x).

Таблица значений функции f(x) может быть интерполирована бесконечным множеством различных функций, поэтому нужно иметь некоторый критерий выбора. Многие интерполирующие функции строятся как линейные комбинации элементарных функций. Линейные комбинации одночленов приводят к алгебраическим полиномам, линейные комбинации тригонометрических функций приводят к тригонометрическим полиномам.

Рассмотрим интерполяцию алгебраическими полиномами.

Интерполяционный полином Лагранжа

Выберем в качестве приближающей функции (х) полином P_n(x) степени n, значение которого совпадают со значениями функции f(x) в узлах интерполяции. Геометрически это задача о построении параболы n–го порядка y=P_n(x), пересекающейся с графиком функции y=f(x) в (n+1)–й наперед заданной точке (рис. 2.1)

Покажем, что такая задача имеет единственное решение.

Пусть

(2.1)

Коэффициенты a_i (i=0,1,2,…n) можно определить из системы уравнений:

(2.2)

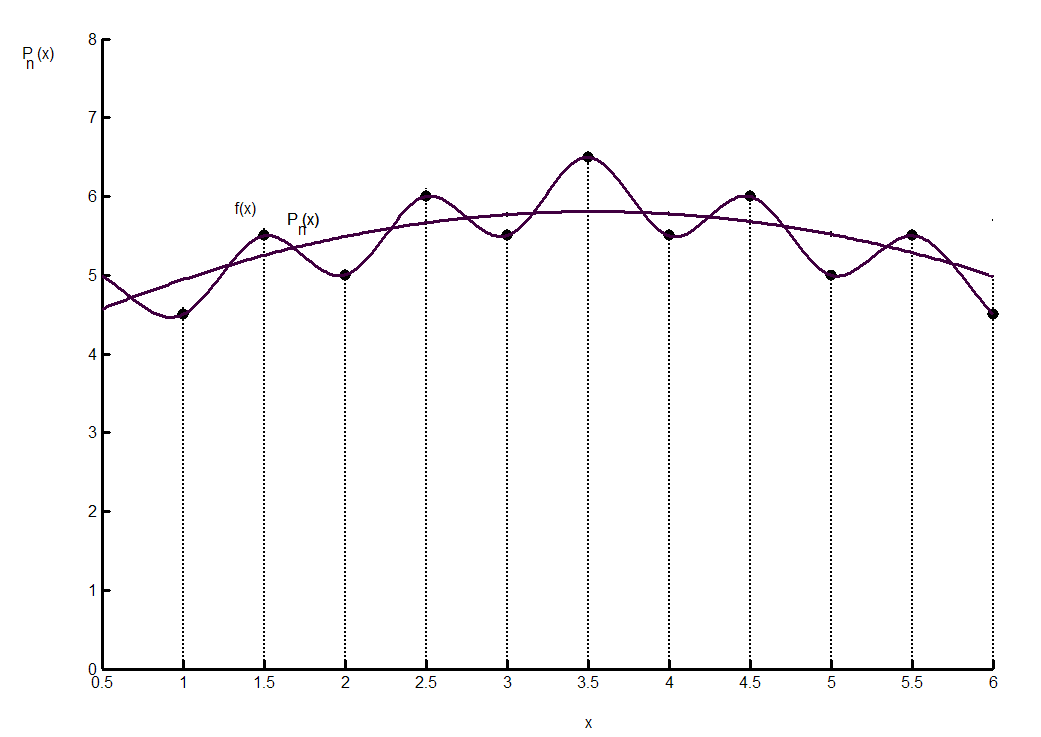
Рис. 2.1. Задача о построении параболы n–го порядка

Определитель этой системы называется определителем Вандермонда.

(2.3)

Если узлы интерполяции различны, то ∆=0 и система уравнений имеет единственное решение.

При определении полинома P_n(x) используют базис Лагранжевых коэффициентов L_i(x) (i=0,1,…n) степени n такие, что

Определим L_i(x) как многочлен степени n обращающийся в 0 в точках

x₀,x_1,…x_i–1,x_i+1,…x_n и равной единице в точке x_i.

Можно показать, что

(2.4)

Полином у_iL_i(x) принимает значение у_i в точке x_i и равен нулю во всех точках х_j . Лагранжевы коэффициенты L_i(x) называют ещё множителями влияния соответствующих узлов интерполирования.

Интерполирующий полином Лагранжа степени п выражается формулой:

(2.5)

Число арифметических операций для его вычисления пропорционально п².

Если не требуется находить общее выражение для полинома Лагранжа, а нужно только вычислить его значения для конкретных х, то удобно пользоваться интерполяционной схемой Эйткена. Согласно этой схеме выражение (2.6)которое является линейным интерполяционным полиномом для узлов х₀ и х₁.

(2.6)

Для другой пары значения соседних узлов x₁ и х₂ вычисляют аналогично (2.7).

(2.7)

Выражение (2.8) представляет собой квадратичный многочлен, интерполирующий значения у₀ у₁, у₂ соответственно в узлах x₀, х₁, х_2.

(2.8)

Подключая последовательно новые узлы интерполяции, в общем случае получим выражение.

(2.9)

которое будет интерполяционным многочленом Лагранжа, принимающем значения у₀, у₁, у₂… ,у_n соответственно в точках х_о, x₁, x₂, ... ,х_n. Вычисление значения этого полинома в точке х по схеме Эйткена удобно проводить, записывая промежуточные результаты в таблицу 2.1.

Таблица 2.1

xi	yi	Li–1,i	Li–2,i–1,i	Li–3,i–2,i–1,i	Li–4,i–3,i–2,i–1,i	...	L0,…,i
x0	y0
x1	y1	L01
x2	y2	L12	L012
x3	y3	L23	L123	L0123
x4	y4	L34	L234	L1234	L01234
…	...	...	...	...	...	...
xn	yn	Ln–1,n	Ln–2,n–1,n	Ln–3,n–2,n–1,n	Ln–4,n–3,n–2,n–1,n	...	L0,…,n

Описанный рекуррентный процесс интерполяции не требует априорного задания степени интерполяционного полинома. Новые узлы интерполяции подключаются в процессе вычислений.

Интерполяционный полином Ньютона

Укажем форму записи интерполяционного полинома Р_п(х)_, которая допускает уточнение результатов интерполяции последовательным прибавлением новых узлов. При этом будем использовать разделенные разности функции, являющиеся удобным аппаратом при работе с таблично заданными функциями. Пусть для функции f(x) заданы узлы интерполяции х₀, х₁,...х_n: y₀ = f(x₀), y₁ = f(x₁),... y_n = f(x_n) – соответствующие значения функции.

Разделёнными разностями первого порядка называются величины, имеющие смысл средних скоростей изменения функции и вычисляемые по формулам:

	(2.10)
	(2.11)

Аналогично определяются разделённые разности второго порядка:

(2.12)

В общем случае разделённые разности k–го порядка определяются через разделённые разности (k–1)–го порядка по рекуррентной формуле:

(2.13)

Вычисление разделённых разностей удобно проводить в таблице. Пример составления таблицы показан ниже (табл. 2.2).

Таблица 2.2

		Разделенные разности
		1–го порядка	2–го порядка	3–го порядка	4–го порядка
x0	f(x0)
x1	f(x1)	f(x0,x1)
x2	f(x2)	f(x1,x2)	f(x0,x1,x2)
x3	f(x3)	f(x2,x3)	f(x1,x2,x3)	f(x0,x1,x2,x3)
x4	f(x4)	f(x3,x4)	f(x2,x3,x4)	f(x1,x2,x3,x4)	f(x0,x1,x2,x3,x4)

Интерполяционный полином может быть записан через разделенные разности в виде

(2.14)

Записанный полином носит название интерполяционного полинома Ньютона. Он удобен тем, что при добавлении к узлам х_о,х₁, x₂,...,х_п нового узла x_n+1 все вычисленные ранее члены остаются без изменений, а в полиноме добавляется только одно слагаемое.

Ход работы

Для функции заданной таблично, определить интерполяционный полином Лагранжа по схеме Эйткена и интерполяционный полином Ньютона.

Вычислить значение полинома Лагранжа и интерполяционного полинома Ньютона в заданной точке.

Построить на одном графике функции y(x), L₀₁₂₃₄₅(x), P_n(x).

Далее показаны примеры интерполяции по формулам Лагранжа [9].