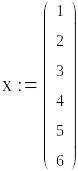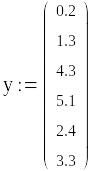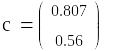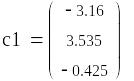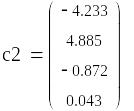МІНІСТЕРСТВО ОСВІТИ І НАУКИ, молоді та спорту УКРАЇНИ

ХЕРСОНСЬКИЙ НАЦІОНАЛЬний ТЕХНІЧНИЙ УНІВЕРСИТЕТ

КАФЕДРА ТЕХНІЧНОЇ КІБЕРНЕТИКИ

Реєстр. №

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

до виконання лабораторних робіт

з дисципліни «Системний аналіз складних систем управління» для студентів 4 курсу напрямків 6.050201 – Системна інженерія і 6.050202 – Автоматика та комп’ютерно-інтегровані технології

Херсон 2012

Методичні рекомендації до виконання лабораторних робіт з дисципліни «Системний аналіз складних систем управління». для студентів 4 курсу напрямку 6.050201 – Системна інженерія за професійним спрямуванням 6.05020101 – Комп’ютеризовані системи управління та автоматики і напрямку 6.050202 – Автоматика та комп’ютерно-інтегровані технології за професійним спрямуванням 6.05020201 – Автоматизоване управління технологічними процесами.

Укладачі: С.О. Рожков, О.В. Полівода. – 81 с. Рос. мовою.

Схвалено методичною комісією кафедри «Технічна кібернетика» спеціальностей 6.05020101 –комп’ютеризовані системи управління та автоматика та 6.05020201 – автоматизоване управління технологічними процесами.

Протокол від « 17 » вересня 2012 р. № 2.

Завідувач кафедри д.т.н., проф.

Марасанов В.В.

Відповідальний за випуск Рожков С.О.

Введение

Дисциплина «Системный анализ сложных систем управления» изучает математический аппарат общей теории систем, а так же методы идентификации систем управления, теории принятия решений, теории эффективности, теории информации и моделирования.

Применение этих методов является обязательным при разработке систем управления сложными системами, а поэтому овладение методами является необходимым условием для современного специалиста в области управления техническими системами.

Во время выполнения лабораторных работ студенты имеют возможность освоить математические пакеты, которые способны производить аналитические математические преобразования – Mathcad и Matlab.

Лабораторные работы 1–3 посвящены методам идентификации систем. В лабораторных работах 4–6 рассмотрены принципы и методы принятия решений в условиях неопределенности и риска. Лабораторная работа 7 посвящена информационному анализу системных задач.

В процессе выполнения лабораторных работ студенты должны оформить отчет по лабораторной работе. Отчет выполняется каждым студентом индивидуально на стандартных листах формата А4. В отчете указывается цель работы, приводятся краткие теоретические сведения по теме работы, результаты выполнения работы, выводы.

Лабораторная работа 1 Регрессионный анализ в среде Mathcad, Matlab, Curve Expert

Цель работы: приобретение практических навыков в аппроксимации функции, заданной таблицей в среде Mathcad, Matlab, Curve Expert.

Теоретические сведения

Регрессионный анализ (линейный) — статистический метод исследования зависимости между зависимой переменной y и одной или несколькими независимыми переменными x1,…,xp [1-–3].

Зависимая переменная — в научном эксперименте измеряемая переменная, изменения которой связывают с изменениями независимой переменной.

Независимая переменная — в эксперименте переменная, которая намеренно манипулируется или выбирается экспериментатором с целью выяснить ее влияние на зависимую переменную.

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии, т. е. требуется определить аналитическое выражение связи между результативным признаком y и факторными признаками x1,…,xp найти функцию:

Построение моделей множественной регрессии включает несколько этапов:

• выбор формы связи (уравнения регрессии);

• выбор факторных признаков;

• обеспечение достаточного объема выборки для получения несмещенных оценок.

Выбор формы связи затрудняется тем, что, используя математический аппарат, теоретически зависимость между признаками может быть выражена большим числом различных функций.

Выбор типа уравнения осложнен тем, что для любой формы зависимости выбирается целый ряд уравнений, которые в определенной степени будут описывать эти связи. Некоторые предпосылки для выбора определенного уравнения регрессии получают на основе анализа предшествующих аналогичных исследований или на базе анализа подобных работ в смежных отраслях знаний.

Поскольку уравнение регрессии строится главным образом для объяснения и количественного выражения взаимосвязей, оно должно хорошо отражать сложившиеся между исследуемыми факторами фактические связи. Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.

Сущность данного метода заключается в том, что большое число уравнений (моделей) регрессии, отобранных для описания связей какого–либо процесса, реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой, главным образом на основе t–критерия Стьюдeнта и F–критерия Фишера. Способ перебора является достаточно трудоемким и связан с большим объемом вычислительных работ. Практика построения многофакторных моделей взаимосвязи показывает, что все реально существующие зависимости между социально–экономическими явлениями можно описать, используя пять типов моделей:

• линейная

• степенная

• показательная

• параболическая

• гиперболическая

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации.

Ход работы

Замечание: Задание к лабораторной работе №1 следует выбрать согласно варианта из задания к лабораторной работе №3.

Аппроксимировать таблично заданную функцию при помощи Matlab:построить сплайн интерполяцию, а также аппроксимирующие функции 1–5 порядков, определить уравнения линий и ошибки аппроксимации.

Открыть программу Curve Expert 1.3 и в появившемся окне занести экспериментальные данные xi и yi.

На панели инструментов программы нажать кнопку “ Run curvefinder” (запустить нахождение кривой).

В появившейся панели нажать кнопку “all On” (все включить) и выбрать порядок полинома.

Программа предложит наилучший вариант регрессионной модели. На панели “User–Defined Model”(определяемая пользователем модель) нажать кнопку “info” и получить уравнение регрессии с числовыми значениями коэффициентов.

Провести интерполяцию исходных данных. Для этого на панели меню нажать кнопку “interpolate”. В появившемся подменю нажать кнопку “polynomial interpolation” (интерполяция по Лагранжу). Далее нажать кнопку “info” и получить уравнение интерполяционного полинома Лагранжа.

Выбрать подходящую модель аппроксимирующую исходные данные. Для этого в меню предусмотрена кнопка “apply fit” (примените пригодный). В появившемся подменю необходимо выбрать подходящую модель аппроксимации.

Произвести сплайн – интерполяцию, аппроксимацию функциями 1–5 порядков, отобразить уравнения линий и ошибки аппроксимации.

Пример выполнения лабораторной работы

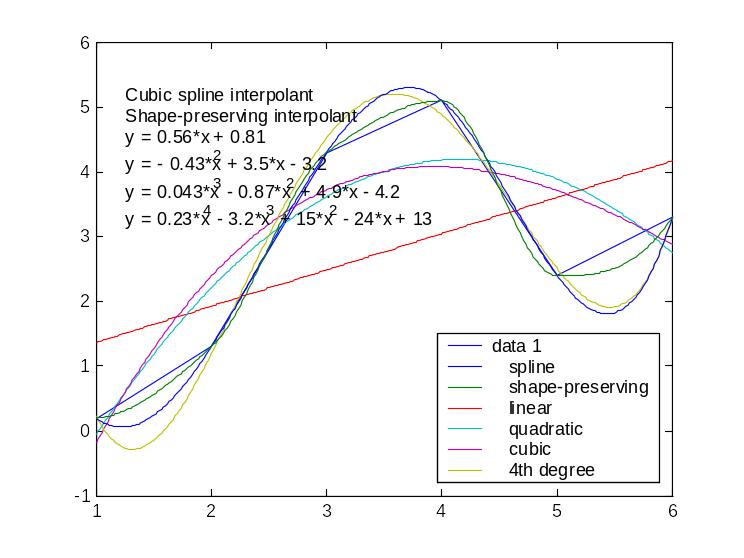
1. Аппроксимация при помощи MATLAB функции, заданной таблично.

Как пример, создадим скрипт m-файла в редакторе MATLAB и введем данные в следующем виде

x=[1 2 3 4 5 6];

y=[0.2 1.3 4.3 5.1 2.4 3.3];

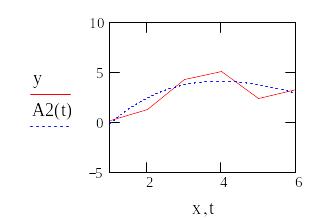
plot(x,y)

После запуска Debug – Run (F5) на экране появляется окно с построенным по введенным точкам графиком.

С помощью меню Tools → Basic Fitting построить сплайн интерполяцию, а также аппроксимирующие функции 1–5 порядков.

Отобразить уравнения линий и ошибки аппроксимации.

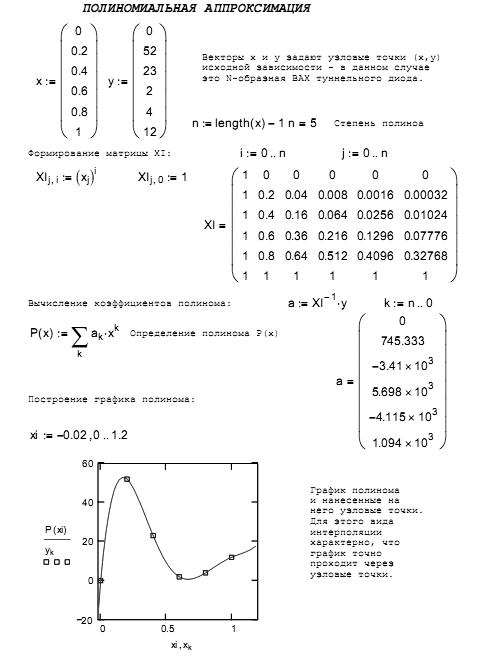
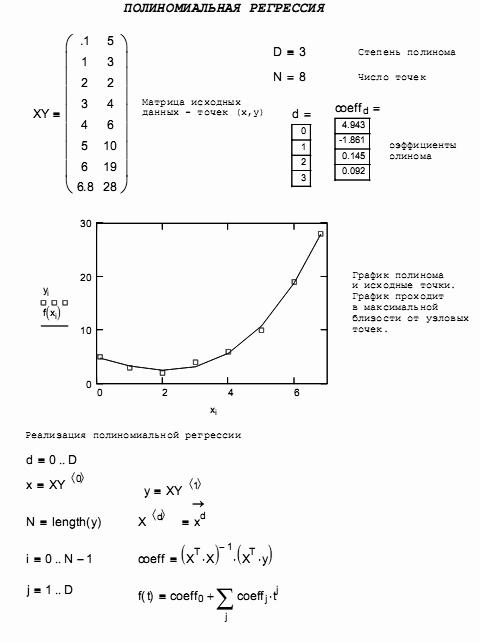
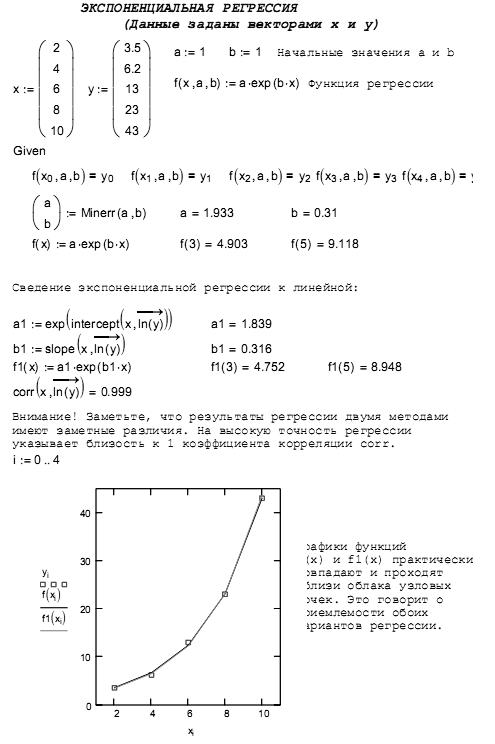
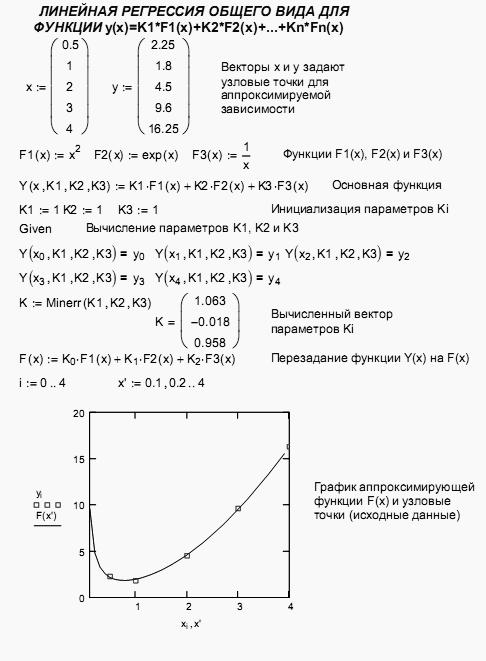
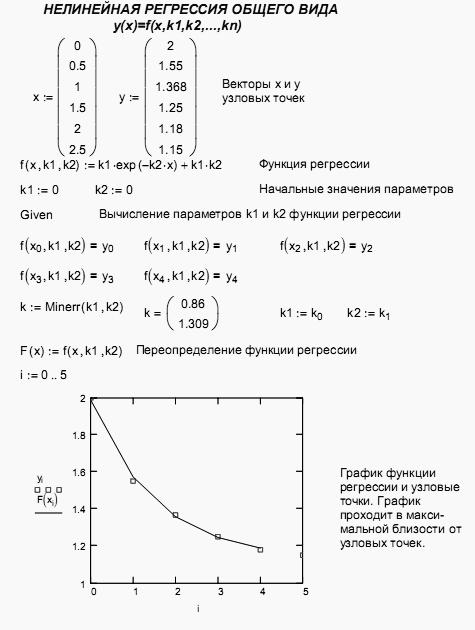
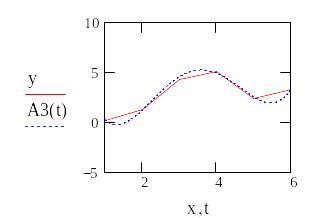
2. Аппроксимация функции заданной таблично в среде Mathcad

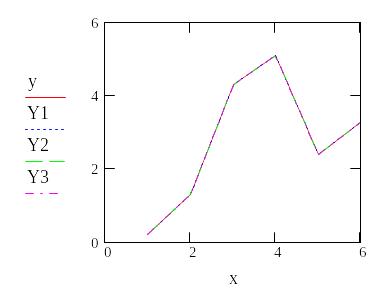
2. Интерполяция степенными полиномами

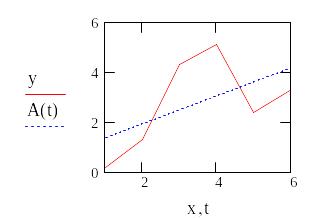
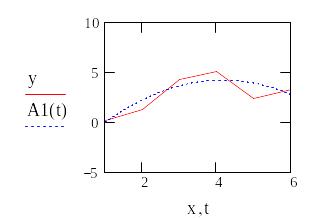
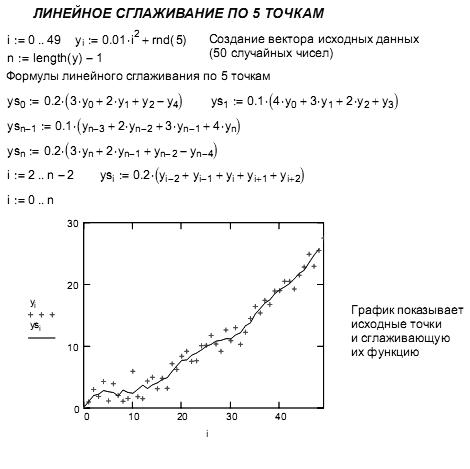
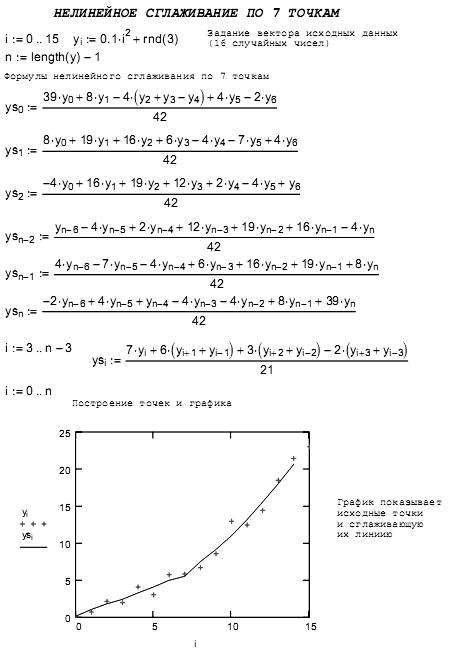
Далее показаны примеры вычислений регрессий и сглаживания данных из [9, 10, 13].