Завдання для самостійного розв’язання.

1. Обчислити значення виразу

при (параметри приймають значення, не рівні між собою).

2. Яке із заданих чисел , 3, є найбільшим та найменшим?

3. Розв’язати рівняння .

4. Довести, що якщо є простим числом, яке відмінне від 2 та 3, то хоча б одне із чисел та не є простим при довільному значенні параметра .

5. При яких значеннях параметра існує єдина пара цілих чисел та , які задовольняють рівняння та систему нерівностей ?

6. Скільки розв’язків має система 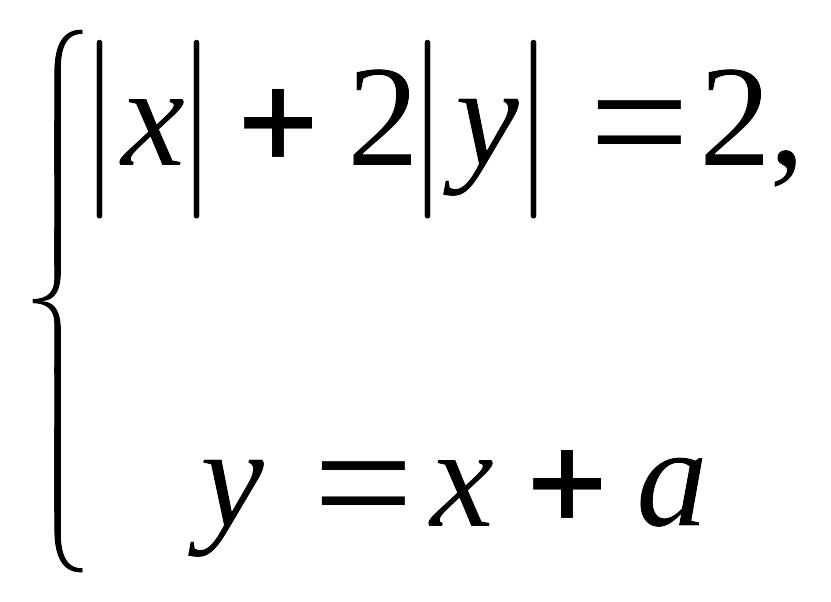у залежності від параметра ?

7. При яких значеннях параметра серед коренів рівняння нема додатних?

8

. Розв’язати рівняння

.

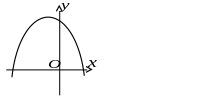
9. Аналізуючи графік функції

, визначити знаки коефіцієнтів (рис.4 та 5).

1

Рис. 5

0. Корені рівняння

Рис. 4

утворюють арифметичну прогресію. При якому значенні це можливо?

11. Корені рівняння утворюють геометричну прогресію. Визначити значення .

12. При яких значеннях параметра а знайдуться такі значення , при яких числа є послідовними членами геометричної прогресії?

13. Знайти всі значення параметра , для кожного з яких пряма, яка проходить через точку , перетинає графік функції у двох точках, сума ординат яких дорівнює .

14. При яких значеннях параметра площа фігури, обмеженої лініями та буде найбільшою?

15. Обчислити значення виразу , якщо .

16. Розв’язати рівняння .

17. При яких значеннях параметра вираз не залежить від параметра , де - корені рівняння .

18. При яких значеннях параметра рівняння має єдиний розв’язок?

19. Відомо, що нерівність виконується при . Знайти всі розв’язки цієї нерівності.

20. При яких значеннях параметра система нерівностей має єдиний розв’язок?

21. При яких значеннях параметра рівняння має рівно два цілих розв’язки?

Розділ 10 Вирази з двома параметрами та їх застосування для складання багатоваріантних завдань

У даному розділі ми повернемося до дослідження проблеми створення компактних за об’ємом дидактичних матеріалів, які дозволяють мати у розпорядженні фактично довільну кількість вправ з окремих тем елементарної математики із відомими відповідями на кожну із них. Як уже відмічалося у вступі (приклад 5), при розв’язуванні рівнянь, нерівностей та їх систем із двома параметрами на координатній площині можна виділити області, у кожній із яких відповідь на задачу задається певними співвідношеннями – деякими функціями від параметрів. Їх можна зобразити на карточці із вказанням загальної відповіді для кожної із областей. Фіксуючи значення кожного із параметрів, ми отримуємо на координатній площині конкретну точку і у залежності від того, в яку область вона попадає, дістаємо відповідь. Для цього у загальні співвідношення, характерні для даної області, підставляємо вибрані значення параметрів. Якщо зафіксувати значення тільки одного із параметрів, то у нашому розпорядженні появиться серія відповідних задач із одним параметром та з готовими відповідями на них. Зауважимо, що процес підготовки конкретних задач за допомогою таких карточок є цілком керованим процесом. Якщо ми, наприклад, хочемо отримати умову для ірраціонального рівняння, у процесі розв’язування якого можуть появитися сторонні корені, достатньо вибрати точку у зоні (якщо така є на карточці) сторонніх коренів. У прикладі 5 вступу – це область 3.

Наведемо ряд прикладів, які ілюструють методику створення таких дидактичних матеріалів.

Приклад 1. Розв’язати рівняння .

Р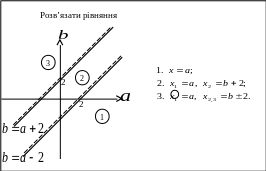 озв’язання. Перепишемо рівняння у виді . Очевидно, що є коренем рівняння, а при інших коренів нема. При дістанемо рівняння з коренями . Одержані значення будуть коренями заданого в умові рівняння, якщо вони задовольняють нерівності . Таким чином, при маємо три корені та ; при - два корені та і при - один корінь . Одержані результати зафіксуємо на карточці.

Розглянемо деякі частинні випадки.

При отримуємо рівняння з коренями при ; та 3 при і єдиним коренем при .

При дістаємо рівняння з коренем , оскільки точка знаходиться в області 1.

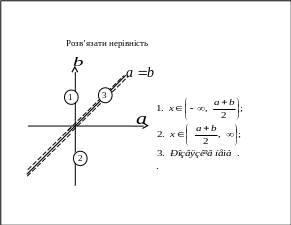
Приклад 2. Розв’язати нерівність .

Розв’язання. Замінимо нерівність рівносильною системою

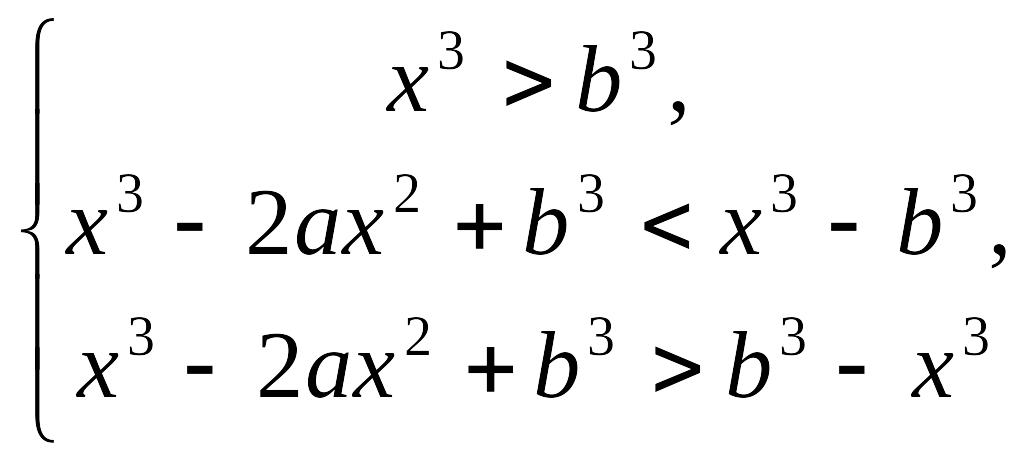
або

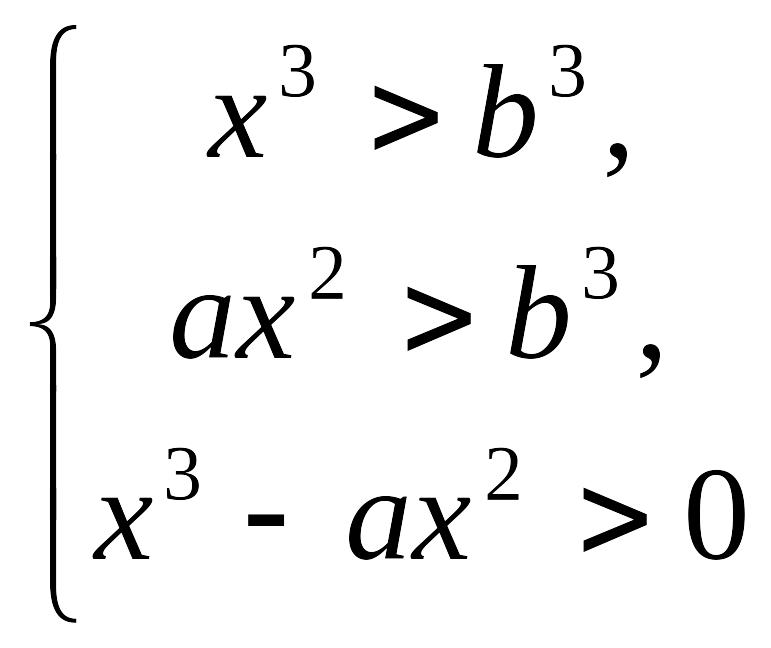
та розглянемо наступні випадки.

1. Якщо , то дістаємо систему

,

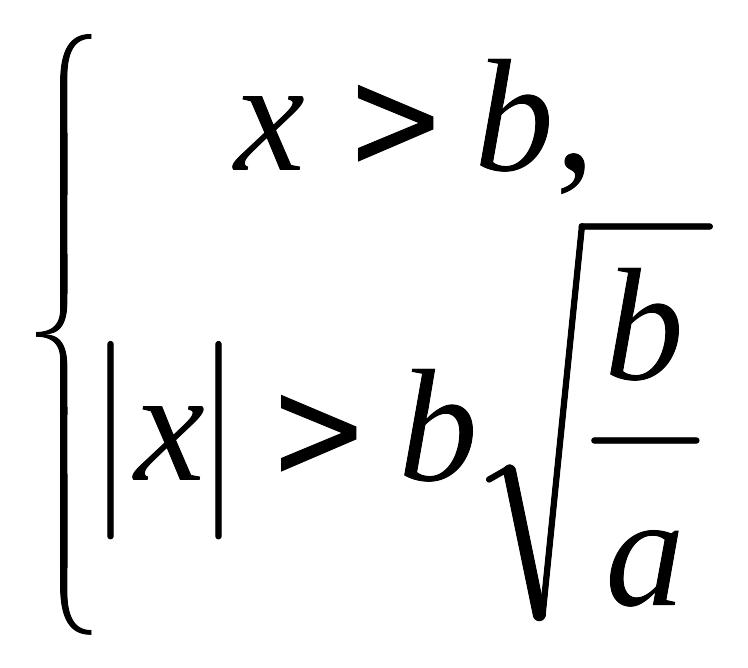звідки , оскільки і .

2. При дістаємо розвязок у виді нерівності .

3. При другу нерівність не задовольняє жодне значення , тому система розв’язків не має.

4. Якщо , то система набуде виду

,

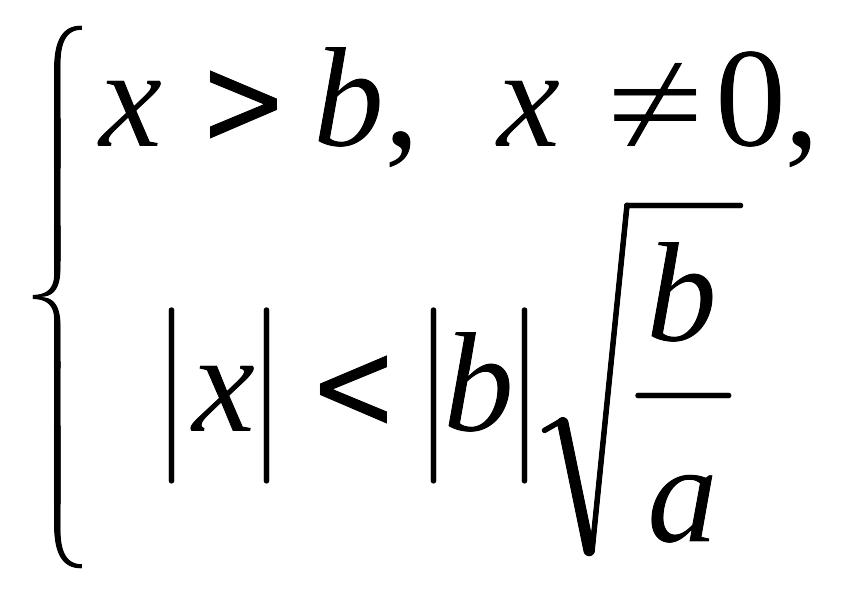звідки дістаємо , оскільки у цьому випадку і .

5. Якщо , то дістаємо систему

.

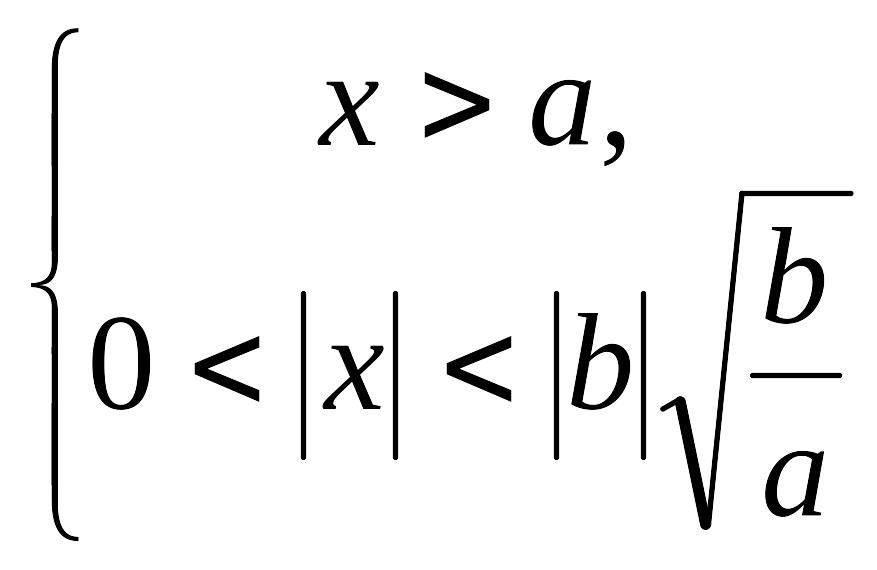Оскільки і тому , то система матиме розв’язки та .

6. При початкова нерівність має вид . Вона рівносильна системі , розглянутій вище у випадку 2.

Отриману вище інформацію про розв’язки нерівності зобразимо на координатній площині .

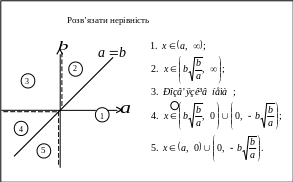
Точки прямої можна відносити до довільної області, яка прилягає до прямої.

Проілюструємо окремі частинні випадки.

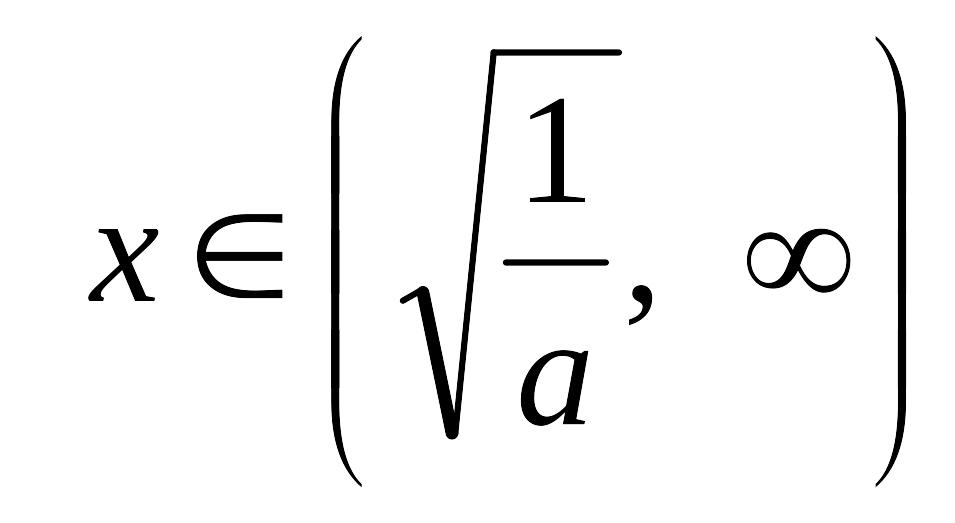При отримуємо нерівність з розв’язками при ; при . При інших значеннях розв’язків нема.

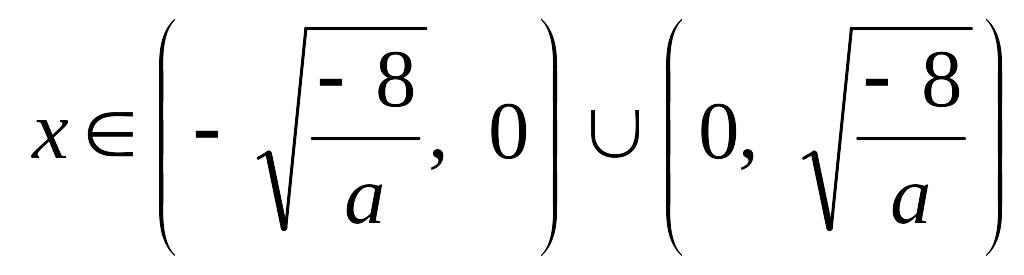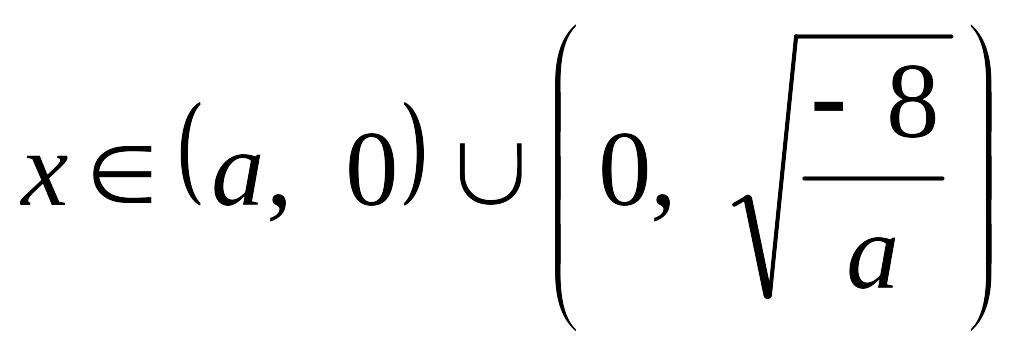Якщо , то маємо нерівність із розв’язками при ; при ; при .

При отримуємо нерівність з розв’язками при ; при .

При маємо нерівність без параметрів . Її розв’язки утворюють інтервал .

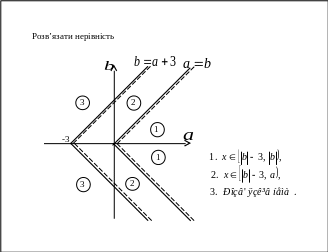
Приклад 3. Розв’язати рівняння .

Розв’язання. Замінимо рівняння рівносильною системою

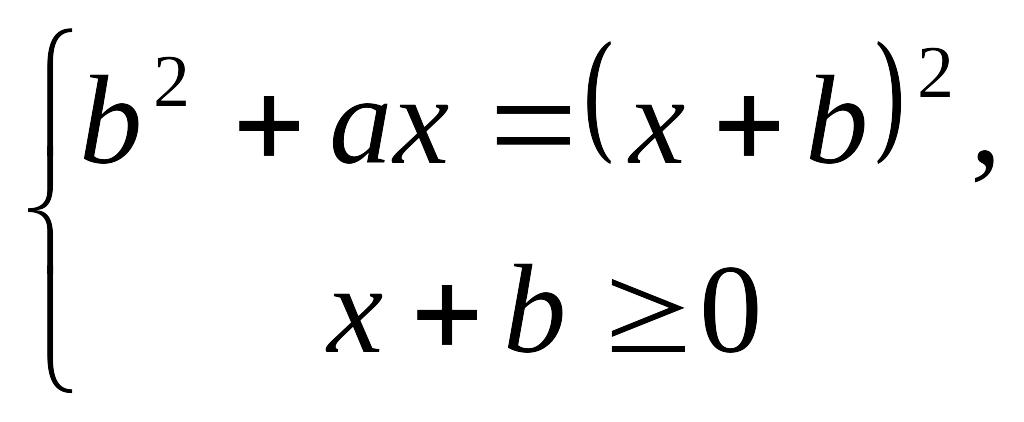
або

.

Корені першого рівняння та будуть розв’язками системи, якщо задовольнятимуть умову . Таким чином, значення буде розв’язком системи при , а значення - при . Користуючись одержаними результатами, складаємо карточку із різними вправами.

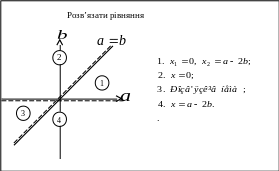
Деякі частинні випадки.

При отримуємо рівняння . Пряма перетинає графік в областях 2 та 1, тому відповідь виглядатиме наступним чином: коренями рівняння буде при , а також , при .

При дістаємо рівняння з коренем , який знаходимо, встановивши, що точка знаходиться в області 4.

Зауважимо, що для точок прямої , розташованих в області 1, корені та співпадають.

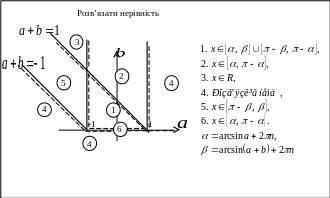
Приклад 4. Розв’язати рівняння .

Розв’язання. У залежності від розташування чисел 0 та на числовій осі можливі наступні 6 випадків:

1) ; 2) ; 3) ; 4) ; 5); ; 6) .

У першому випадку рівняння набуває виду . При воно має розв’язки , а при розв’язків не має.

У випадку 2) рівняння запишеться у виді , звідки . Одержане значення буде розв’язком, якщо задовольняє умову , тобто при .

У третьому випадку рівняння набуває виду . При воно має розв’язки , а при розв’язків не має.

У випадку 4) рівняння запишеться у виді і матиме розв’язки тільки у випадку, коли .

У випадку 5) одержуємо рівняння , звідки . Це значення буде розв’язком, якщо задовольняє умову , або .

Останній шостий випадок приводить до рівняння , яке при має розв’язки , а при розв’язків не має. Окремо зауважимо, що при розв’язком рівняння буде довільне .

Одержані результати виносимо на координатну площину .

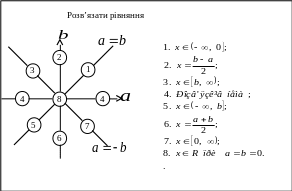
Для точок прямих та відповіді вказано на карточці.

Розглянемо частинні випадки при деяких конкретних значеннях параметрів.

Нехай . Рівняння матиме вид . Пряма перетинає графік по зонах 4, 3, 2, 1, 4. Залежно від областей, де вона проходить, одержуємо відповідь: при розв’язків нема; при ; при ; при .

Нехай . Рівняння має вид . Точка знаходиться у зоні 4, а для даної області рівняння розв’язків не має.

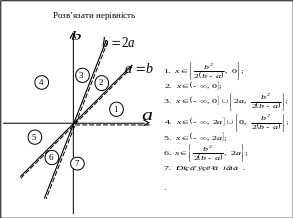
Приклад 5. Розв’язати нерівність .

Розв’язання. Замінимо нерівність рівносильною сукупністю двох систем

та ,

звідки отримуємо

та .

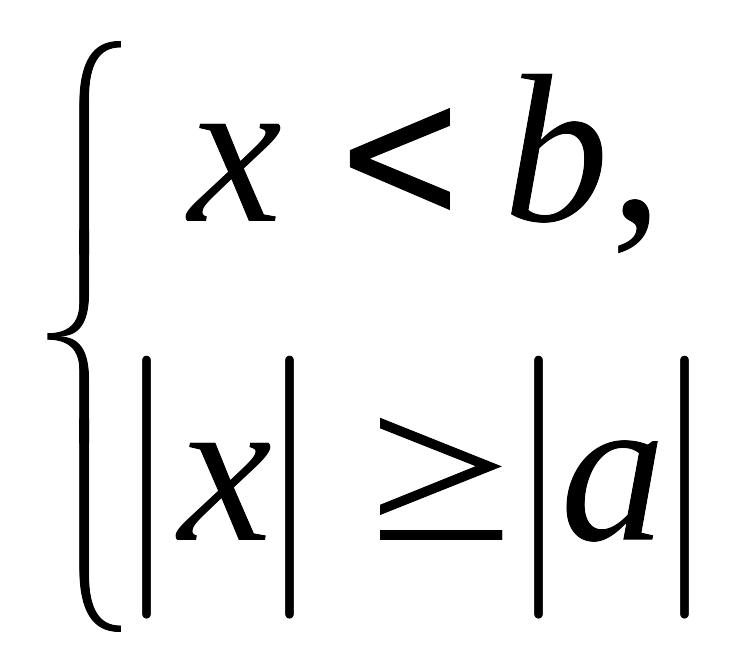Для відшукання розв’язків одержаних систем обмежимося розглядом випадку , оскільки параметр входить у запис нерівності у парному степені. Розглянемо наступні випадки.

1). Якщо , то виконується умова і розв’язками нерівності будуть ті значення , для яких .

2). При дістаємо, що і розв’язками нерівності будуть та .

3). Нехай . Тоді виконуватиметься нерівність і розв’язками заданої нерівності будуть .

4). У випадку, коли дістаємо , що дозволяє отримати розв’язки нерівності у виді .

Одержані результати зведемо у наступну карточку.

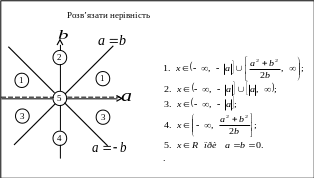
Точки прямих та можна відносити до довільної області, яка до них прилягає.

Розглянемо частинні випадки.

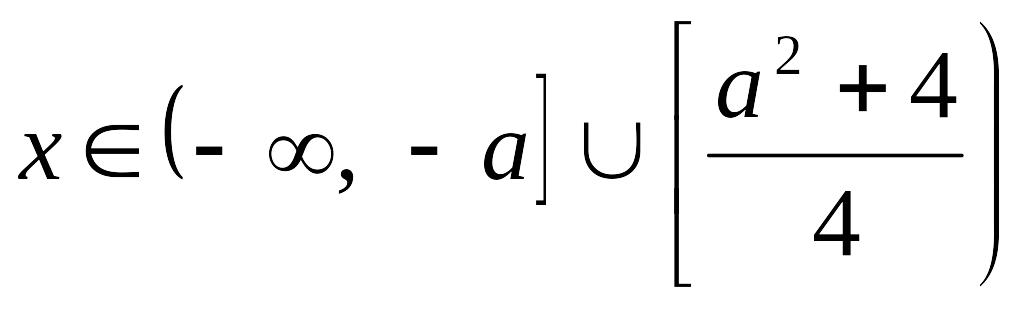Нехай . Нерівність набуде виду . Пряма перетинає графік в областях 1, 2 та 1. Прослідковуючи, в яких областях вона проходить, записуємо відповідь: при ; при .

Нехай . Нерівність запишеться у виді . Точка знаходиться в області 1, тому відповідь отримуємо у виді .

Приклад 6. Розв’язати рівняння .

Розв’язання. Розглянемо наступні випадки.

1). Нехай .

Тоді при рівняння запишеться у виді і матиме розв’язки при . Якщо , то розв’язків у цьому випадку не буде.

При отримуємо рівняння з розв’язком при умові, що виконується нерівність тобто .

При дістаємо рівняння , яке матиме розв’язки при та не матиме розв’язків при .

2). При рівняння має розв’язки при та не матиме розв’язків при .

3). Нехай . Тоді .

При дістаємо рівняння з розв’язками при . Якщо , то розв’язків у цьому випадку не буде.

При отримуємо рівняння . Значення буде розв’язком при умові, що виконується нерівність тобто .

При дістаємо рівняння , яке матиме розв’язки при та не матиме розв’язків при .

Одержані результати заносимо у наступну карточку.

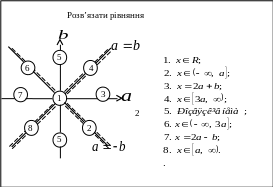
Розглянемо частинні випадки.

Нехай . Рівняння набуває виду . Пряма перетинає графік по областях 7, 6, 5, 4 та 3. У залежності від області, де вона проходить, отримуємо відповідь: при ; при ; при розв’язків нема; при ; при .

Нехай . Рівняння запишеться у виді . Точка знаходиться в області 3, тому відповідь отримуємо у виді .

Зрозуміло, що аналогічні карточки можна складати і з інших тем. Наведемо зразки ще декількох карточок, не пропонуючи міркувань, які приводять до їх створення.

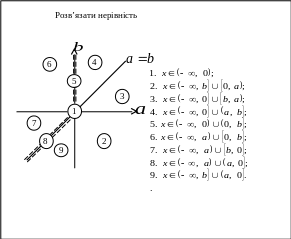
Відповіді

Розділ 1. 1. При . 2. . 3. . 4. При жодному. 5. При . 6. При . 7. та . 8. . 9. . 10. . 11. та при ; при ; при . При інших значеннях розв’язків нема. 12. . 13. . 14. . 15. . 16. Вказівка. Використати теорему Вієта для коренів обох рівнянь 17. . 18. . 19. -21. 20. Якщо , то . Якщо , то . Тут , . При інших значеннях корені не існують. 21. та при ; та при ; та при ; , та при ; та при . 22. . 23. Мінімальне значення , максимальне значення . 24. . 25. . 26. та . 27. . 28. . 29. . 30. .

Розділ 2. 1. . 2. . 3. . 4. Вказівка. Функція у точках та приймає значення різних знаків. 5. . 6. . 7. . 8. 11 при . 9. при . 10. . 11. При та довільному , або при .12. . 13. . 14. при . Для інших значень критичних точок нема. 15. При таких інтервалів нема. При зростає на проміжку . При зростає на всій числовій осі. 16. та . 17. . 18. . 19. . 20. або . 21. . 22. при . При інших значеннях розв’язків нема. 23. та при . При інших значеннях розв’язків нема. 24. при . При інших значеннях розв’язків нема. 25. .

Розділ 3. 1. . 2. . 3. та 100 при . При інших розв’язків нема. 4. при . Для інших розв’язків нема. 5. . 6. . 7. . 8. при . Для інших розв’язків нема. 9. або . 10. . 11. . 12. . 13. . 14. При жодному. 15. та .

Розділ 4. 1. Чотири при , три при , два при та при . При жодного. 2. Чотири при , три при , два при та при . При жодного. 3. Один при , два при . 4. Два при , один при . При жодного. 5. Два при , чотири при , три при . 6. . 7. . 8. Відповідь. 4 при та ; 8 при ; 6 при ; 2 при . При інших розв’язків нема. 9. 2 при ; 4 при та ; 6 при ; 8 при . При інших розв’язків нема. 10. . 11. . 12. . 13. . 14. та . 15. . 16. . . 17. та . 18. . 19. . 20. При та . 21. . 22. та . 23. .24. та . 25. та . 26. та . 27. . 28. Один при та ; два при , та ; три при . При інших розв’язків нема. 29. Два при , безліч при . При інших значеннях розв’язків нема.

Розділ 5. 1. при . При та . При інших розв’язків нема. 2. при . При та . При інших розв’язків нема. 3. при . При інших розв’язків нема. 4. Множина точок, розташованих нижче від параболи . 5. . Корені існують при . При відстань між коренями найбільша і дорівнює 6. 6. та при . При інших розв’язків нема. 7. при . При інших розв’язків нема. 8. при , при . 9. Частину площини , для точок якої виконується нерівність . 10. . 11. .

Розділ 6. 1. та при та ; при . 2. та при ; при ; при ; при . 3. та при ; , якщо або ; при . 4. та при ; , якщо ; при ; при ; , якщо . 5. . 6. . 7. та . 8. Вказівка. Розглянути вирази та . 9. . 10. . 11. . 12. . 13. При . 14. при ; та при ; при . 15. Два при , один при та жодного при інших значеннях . 16. Три при , один при . 17. При , або , або . 18. при ; при ; та при ; при . 19. при ; при ; та при ; при . 20. , . Вказівка. Записати ліву частину рівняння у виді , де - корінь рівняння, - знаменник прогресії, та прирівняти коефіцієнти многочленів. 21. .

Розділ 7. 1. та . 2. При . 3. . 4. . 5. 1. 6. . 7. . 8. 3. 9. та при ; при ; при розв’язків нема. 10. при ; при ; при , де ; при . При інших значеннях розв’язків нема. 11. при ; при , де . При інших значеннях розв’язків нема. 12. . Допустимими значеннями параметра є відрізок . 13. та . 14. . 15. при ; при ; при , . 16. при ; та при ; при . 17. при ; при інших розв’язків нема. 18. при ; та при . 19. . 20. при . При інших розв’язків нема. 21. . 22. Два при та при , один при . 23. при . При інших значеннях параметра розв’язків нема. 24. . 25. . 26. при ; при розв’язків нема. 27. При ; при . 28. . 29. . 30. . 31. при ; при . При розв’язків нема. 32. При ; при . При інших розв’язків нема. 33. . 34. при . 35. . 36. . 37. при . При розв’язків нема. 38. при ; при . 39. при ; при ; при . 40. , . 41. при ; при . 42. .

Розділ 8. 1. . 2. . 3. . 4. . 5. . 6. . 7. . 8. . 9. . 10. . 11. . 12. . 13. . 14. . 15. . 16. При розв’язками будуть пари та , а якщо - то та . При інших розв’язків нема. 17. якщо та , якщо . При інших розв’язків нема. 18. та . 19. . 20. . 21. Чотири при , два при та , три при або . 22. та . 23. При 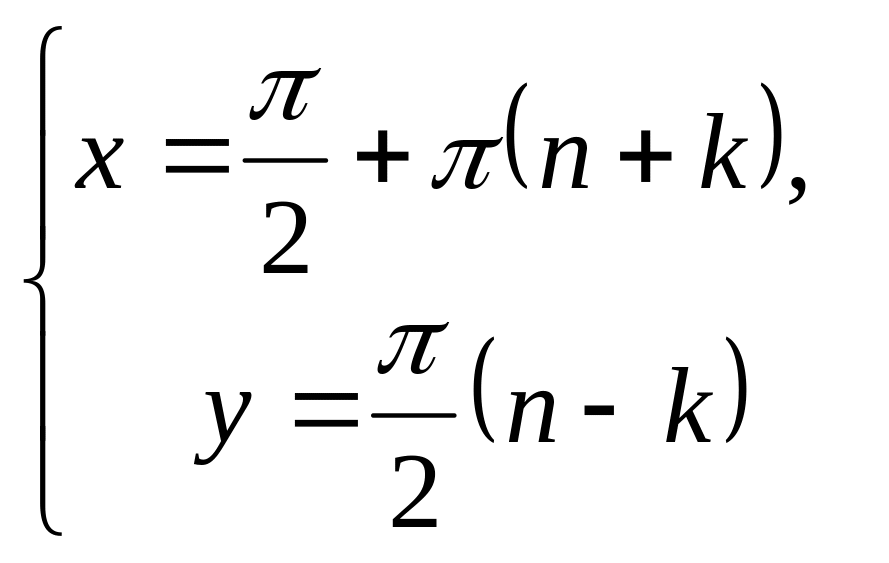, . При інших розв’язків нема. 24. . 25. .

Розділ 9. 1. 1. 2. При найменшим є число , а найбільшим число . При навпаки. При всі три числа рівні. 3. Три корені та 3 при , два корені та 3 при , один корінь при . 4. Вказівка: розглянути випадки . 5. . 6. Два розв’язки при , один розв’язок при . При інших розв’язків нема. 7. . 8. . 9. На рис. 3 , . На рис. 4 , . 10. . 11. . 12. . 13. . 14. . 15. , якщо . Для інших значень задача поставлена некоректно, оскільки вираз при жодному . 16. При , при , . При інших розв’язків нема. 17. . 18. та . 19. . 20. . 21. .