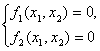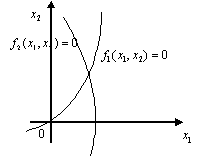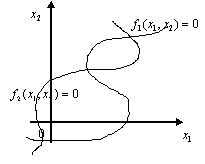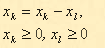6. Численное решение систем линейных алгебраических уравнений (метод Гаусса; метод итераций).

Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

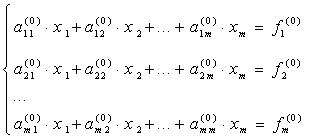
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x₁ из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим

.

Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

.

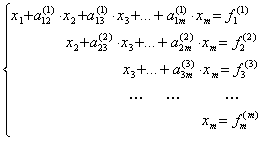Из нее в обратном порядке находим все значения x_i:

.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

, j = i+1,i+ 2, …, m;

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁ был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁ из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:

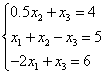
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:

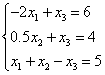
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:

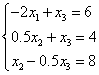
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:

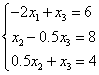
Исключим из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:

Обратный ход: .

Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.

Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.

Метод простой итерации или метод Якоби

Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

где , , .

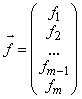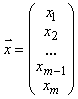Предположим, что диагональные элементы матриц A исходной системы не равны 0 (a_ii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(1),

Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:

(2)

Аналогично находятся следующие приближения , где в (2) вместо необходимо подставить .

Или в общем случае:

. (3)

или

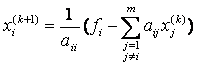
Условие окончания итерационного процесса .

Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .

Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.

Пример.

Решить систему линейных уравнений с точностью :

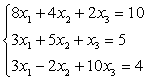
	8	4	2		10		x1
=	3	5	1	=	5	=	x2
	3	–2	10		4		x3

Решение прямыми методами, например, обратной матрицей, даёт решение:

.

Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .

Приводим систему уравнений к виду (1):

.

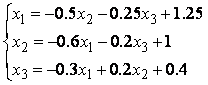Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:

k	x1	x2	x3	точность
0	0	0	0
1	1.250	1.000	0.400	1.2500
2	0.650	0.170	0.225	0.8300
3	1.109	0.565	0.239	0.4588
	………
4	0.908	0.287	0.180	0.2781
5	1.061	0.419	0.185	0.1537
6	0.994	0.326	0.165	0.0931
7	1.046	0.370	0.167	0.0515
8	1.023	0.594	0.160	0.2235
9	0.913	0.582	0.212	0.1101
10	0.906	0.505	0.242	0.0764
11	0.937	0.495	0.229	0.0305
12	0.945	0.516	0.218	0.0210
	……
13	0.937	0.523	0.220	0.0077

Здесь

,

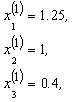
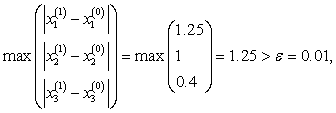
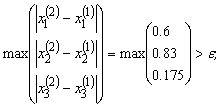
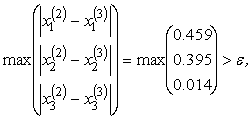
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.

Следовательно, приближенное решение имеет вид:

7. Численное решение нелинейных уравнений (метод простой итерации для решения нелинейных уравнений; метод Ньютона; решение систем нелинейных уравнений: решение обыкновенных дифференциальных уравнений).

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Дано нелинейное уравнение:

Необходимо решить это уравнение, т. е. найти его корень  .

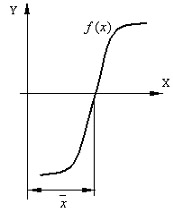
Если функция имеет вид многочлена степени m,

где a_i - коэффициенты многочлена,  , то уравнение f(x)=0 имеет m корней

Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x, то уравнение называется трансцендентным уравнением.

Примеры:

Такие уравнения обычно имеют бесконечное множество решений.

Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений.

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности. Для этого используются приближенные (численные) методы решения.

Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b], в котором лежит уточняемый корень уравнения

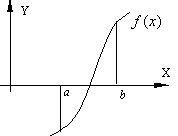
Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b)<0, то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

1. отделение корней, - т.е. определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;

2. уточнение корней, - т.е. сужение интервала [a,b] до величины равной заданной степени точности  .

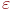Метод простых итераций.

В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).

Пусть с точностью   необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду

(4.2)

В качестве начального приближения 0 выбираем любую точку интервала [a,b].

Далее итерационный процесс поиска корня строится по схеме:

(4.3)

В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие

(4.4)

или число итераций превысит заданное число N.

Для того, чтобы последовательность х₁, х₂,…, х_n приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:

(4.5)

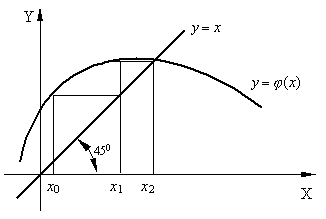
Рис. 4.6.  Геометрический смысл метода

Метод Ньютона (метод касательных).

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Дано нелинейное уравнение:

f(x)=0

Найти корень на интервале [a,b] с точностью  .

Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня (Рис. 4.8).

Выберем начальную точку x₀=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корняx₁.

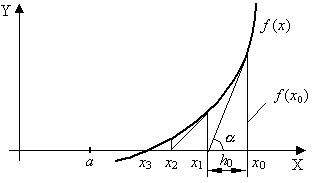
Рис. 4.8. 

x₁ = x₀ – h₀,

где

Поэтому

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой

(4.6)

Процесс поиска продолжаем до тех пор, пока не выполнится условие:

(4.7)

Упростим условие (4.7), исходя из (4.6). Получим:

(4.8)

Метод обеспечивает быструю сходимость, если выполняется условие:

(4.9)

т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x₀) и ее кривизны f"(x₀) совпадают.

Модифицированный метод Ньютона (метод секущих).

В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

Тогда рекуррентная формула (4.6) будет иметь вид:

(4.10)

где 

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Задача решения систем нелинейных уравнений часто встречается на практике. Достаточно вспомнить, что решение нелинейных краевых задач (как для обыкновенных дифференциальных уравнений, так и для уравнений с частными производными) методом конечных разностей, а также минимизация функций многих переменных численными методами приводят к нелинейным системам уравнений.

Требуется найти приближенное решение системы нелинейных уравнений:

(3.1)

где  – заданные функции   переменных  . Здесь под решением понимается такой набор вещественных чисел  , что при подстановке их в (3.1) получаются тождества.

Систему (3.1) можно представить в векторном виде:

,

где

,  .

(3.2)

Как видно из (3.1), при   имеет место случай одного нелинейного уравнения.

При численном решении системы (3.1) неизбежно возникает вопрос о существовании решения и его единственности. В общем случае ответить на этот вопрос очень сложно. В случае системы двух нелинейных уравнений ( ):

(3.3)

ответ на вопрос о существовании решения можно, в принципе, найти геометрическим способом. Для этого на плоскости   нужно изобразить графики функций и . Точки пересечения графиков и дадут множество решений системы (3.3).

Несколько возможных ситуаций в случае   представлено на рис.3.1.

Случай  :

Единственное решение	Несколько решений	Нет решений

Рис. 3.1

В дальнейшем предполагается, что система нелинейных уравнений (3.1) имеет интересующее нас вещественное решение

,

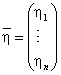хотя оно может быть и не единственным.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

 

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x, y, y ',  y '',  …  , y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия.

 

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 

Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 

Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

 

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

 

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

 

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Для решения уравнений, которые не интегрируются в квадратурах, применяются приближенные или численные методы.

8. Численные методы оптимизации (глобальная, локальная и безусловная оптимизация; оптимальное и рациональное решения; поиск минимума функции одной переменной; поиск минимума функции многих переменных, методы спуска).

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Теорию и методы решения задачи оптимизации изучает математическое программирование.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^*, который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:

1. Допустимое множество — множество  ;

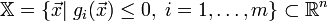2. Целевую функцию — отображение  ;

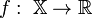3. Критерий поиска (max или min).

Тогда решить задачу   означает одно из:

1. Показать, что  .

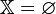2. Показать, что целевая функция 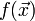  не ограничена снизу.

3. Найти  .

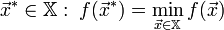4. Если 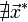 , то найти  .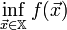

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек   таких, что всюду в некоторой их окрестности   для минимума и   для максимума.

Если допустимое множество  , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).^[1]

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

• Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

• Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

1. детерминированные;

2. случайные (стохастические);

3. комбинированные.

По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.

По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:

• Задачи оптимизации, в которых целевая функция   и ограничения 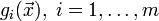  являются линейными функциями, разрешаются так называемыми методами линейного программирования.

• В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:

  • если   и   — выпуклые функции, то такую задачу называют задачей выпуклого программирования;

  • если 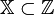 , то имеют дело с задачей целочисленного (дискретного) программирования.

По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:

• прямые методы, требующие только вычислений целевой функции в точках приближений;

• методы первого порядка: требуют вычисления первых частных производных функции;

• методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.

Помимо того, оптимизационные методы делятся на следующие группы:

• аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);

• численные методы;

• графические методы.

В зависимости от природы множества X задачи математического программирования классифицируются как:

• задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;

• задачи целочисленного программирования — если X является подмножеством множества целых чисел;

• задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.

• Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование.

Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

• Определение границ системы оптимизации

  • Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается

• Выбор управляемых переменных

  • «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)

• Определение ограничений на управляемые переменные

  • … (равенства и/или неравенства)

• Выбор числового критерия оптимизации (например, показателя эффективности)

  • Создаём целевую функцию

В настоящее время известны следующие методы решения задач оптимизации, суть которых определяется ее математической формулировкой:

Методы исследования функций классического анализа, применяемые в случаях, когда аналитический вид критерия оптимальности известен, ограничения отсутствуют и возможно аналитическое или численное решение.

Методы, основанные на использовании неопределённых множителей Лагранжа, применяемые для решения задач оптимизации с ограничениями типа равенств

Методы вариационного исчисления, используемые для решения задач статической и динамической оптимизации, в которых критерий оптимальности представлен в виде функционала, а решение заключается в отыскании вида функции.

Принцип максимума Понтрягина, применяемый для решения задач оптимального управления объектами, описываемыми системами дифференциальных уравнений, причем на управление наложены ограничения, а решение отыскивается в виде разрывных функций.

Метод динамического программирования, являющийся эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых критерий оптимальности является аддитивной функцией критериев оптимальности отдельных стадий, ограничения же на переменные учитываются при решении частных задач оптимизации на каждой стадии.

Методы математического программирования, включающие в себя методы линейного и нелинейного программирования, причем методы линейного программирования используются для решения задач, в которых критерий оптимальности и ограничения сформулированы в виде линейных алгебраических выражений.

Предполагая, что задача оптимизации некоторым образом определена, можно классифицировать методы оптимизации по способам решения задач следующим образом.

Аналитические методы, использующие классические методы дифференциального и вариационного исчислений. Эти методы заключаются в определении экстремума целевой функции путем нахождения тех значений переменных, которые обращают в ноль ее первые производные.

Численные методы, использующие предшествующую информацию для нахождения лучших решений при помощи итерационных процедур. Численные методы применяются для решения задач, которые не могут быть решены аналитически, и, поскольку достаточно часто практические задачи поддаются решению численными методами.

Графические методы, основанные на графическом изображении подлежащей максимизации или минимизации функции, зависящей от одной или двух переменных. Экстремум функции в этом случае получают непосредственно путем анализа ее графического изображения.

Экспериментальные методы. Экстремум функции находится путем в результате эксперимента непосредственно на реальном объекте. Результаты проведенного эксперимента используются для планирования следующего эксперимента, позволяющего получить лучшие результаты.

Методы исследования различных вариантов, основанные на анализе нескольких возможных решений одной и той же задачи с целью выбора наилучшего.

При проектировании изделий, как правило,  исходят из необходимости учитывать различные требования. Применительно к деформируемым механическим конструкциям таковыми являются прочность, жесткость, устойчивость и т.д.

Решение, которое удовлетворяет всем заданным ограничениям, называется допустимым. Из допустимых в процессе решения экстремальных задач выбираются оптимальные или рациональные решения.

Под оптимальным будем понимать такое допустимое решение, которое является наилучшим с точки зрения выбранного критерия оптимальности.

Критерий оптимальности формируется на основе одного или нескольких критериев эффективности. Критерием эффективности может быть: масса, стоимость, приведенные затраты, срок изготовления и т.п. Но не все критерии эффективности и ограничения, выражающие требования к проектируемым изделиям, могут быть формализованы, например, эстетичность, компактность, технологичность изготовления и пр. Такие критерии эффективности и ограничения анализируются путем качественной оценки проектируемого изделия экспертами в области эстетики, компоновки, технологии и т.п. В этом случае целесообразно ввести понятие рационального решения.

Под рациональным будем понимать такое решение, которое получается неформальным путем, т.е. с учетом экспертных (или других неформальных) оценок.

При поиске оптимальной конструкции по принятому критерию оптимальности и ограничениям можно получить оптимальную, но нерациональную конструкцию. Например, если требование технологичности не нашло количественной оценки и не вошло в число ограничений, то можно получить проект минимального веса (оптимальный по весу), но нерациональный проект в силу нетехнологичности. Более тяжелая конструкция, но удобная с технологической точки зрения, может оказаться более рациональной.

Применительно к деформируемым механическим конструкциям рациональное проектирование может быть определено как проектирование, основанное на принципах механики деформируемого твердого тела и имеющее целью получение оптимальной конструкции на базе выбранного проектантом критерия. Оптимизационные задачи (и их различные постановки) представляют собой отдельные подзадачи в процессе разработки в целом рационального проекта.

Для решения задачи оптимизации необходимо иметь множество возможных (альтернативных) решений Y. Решение называют допустимым, если оно удовлетворяет ограничениям (требованиям, предъявляемым к объекту): ресурсным, социальным и т.д. При этом

Y д ⊆ Y,

где символ ⊆ означает, что множество Y д есть часть или совпадает с множеством Y возможных решений.

В множестве допустимых решений можно выделить множество эффективных решений Y э , которое включает в себя несравнимые между собой наилучшие решения (несколько таких решений):

Y э ⊆ Y д .

В множестве эффективных решений есть одно оптимальное решение, которое надо найти. Решение Y о называется оптимальным, если оно обеспечивает экстремум (максимум, минимум) одновременно всех критериев. Оптимальное решение находится в множестве эффективных решений:

Y о ⊆ Y э .

Поскольку все критерии одновременно не могут принять экстремальные значения (мощность – минимальная, производительность – максимальная, уровень шума – минимальный, стоимость –

минимальная и т.д.), то при решении многокритериальной задачи находят только одно рациональное решение. Таким образом, задача оптимизации направлена на определение наилучшего (рационального) решения, путем последовательного сужения множеств Y, Y д , Y э в соответствии с допустимыми ограничениями и принятыми критериями:

Y о ⊆ Y э ⊆ Y д ⊆ Y.

Чем больше подобрано альтернативных вариантов, и чем более удачно подобраны критерии, тем больше вероятность того, что найденное решение будет самым лучшим.

Субъектом всякого решения является лицо, принимающее решение (ЛПР). Это собирательное понятие, включающее как одно индивидуальное лицо, так и группу лиц (групповое ЛПР).

ЛРП осуществляет выбор решения. Выбор – это ключевая процедура процесса оптимизации. Выбор может быть критериальный, волевой и случайный. С помощью критериев решаются одно- и многокритериальные задачи. Выбор с помощью критериев – самый точный. Волевой выбор решения представляет собой осознанный и ответственный выбор в условиях, когда отсутствует полный комплекс критериев. Случайный выбор применяется при полном незнании критериев

оценки. Им можно пользоваться, когда область допустимых решений минимальна.

Для облегчения процесса выбора, исследуемые варианты оцениваются количественно и качественно. Количественное измерение важности и предпочтительности вариантов решений выполняется методом ранжирования.

Ранжирование – это процедура упорядочения. Выполняется она ЛПР. При ранжировании варианты решений расставляются в порядке предпочтения по отношению к каждому критерию.

Если среди вариантов нет эквивалентных (равнозначных) решений, то из них можно составить последовательность

mх х х х f f f f ... 3 2 1 , (1)

где вариант х 1 более предпочтителен из всех вариантов; вариант х 2 менее предпочтителен х 1 , но предпочтительнее всех остальных и т.д.

Отношение (1) можно записать отношением чисел

с 1 > с 2 > с 3 >… > с m .

Возможна обратная последовательность чисел

с 1 < с 2 < с 3 <… < с m . (2)

Если наиболее предпочтительному варианту присвоить число 1, то получим числовую последовательность

1 < 2 < 3 <…< m. (3)

Здесь числа 1, 2, 3,…m называют рангами.

При ранжировании наиболее предпочтительному варианту присваивается ранг, равный единице, второму по предпочтительности – ранг, равный двум и т.д. Для эквивалентных вариантов назначаются одинаковые ранги, равные среднему арифметическому значению рангов. В этом случае, например, ранги r 1 =r 2 = r 3 = (3+4+5)/3 = 4.

Выбор решений – это заключительный и наиболее ответственный этап процесса принятия решений. Выбор выполняют путем последовательного сужения области решений и уменьшения неопределенностей. При этом множество допустимых вариантов решений сужается до множества эффективных вариантов решений. Процедура эта выполняется следующим образом.

Пусть множество допустимых решений содержит варианты Y 1 , Y 2 ,… Y 8 . Для оценки вариантов подобраны критерии вариантов А 1 , А 2 ,… А 6 .

Для определения эффективных решений значения всех критериев развития по вариантам приводят к рангам, и результаты заносят в таблицу.

Сначала ранжируют варианты решений по критерию А 1 . Для этого надо определить: в каком решении критерий А 1 наилучшим образом реализован. В приведенном примере предпочтение отдано варианту Y 1 , и ему присвоен ранг 1. Остальные варианты решений менее предпочтительны, и им присвоены ранги в пределах 2…5. Затем решения ранжируют последовательно по остальным критериям.

Определение области эффективных решений делается путем попарного сравнения вариантов решений. Сравнение выполняются по принципу Парето, согласно которому одно решение Y i предпочтительнее другого решения Y j, если выполняется векторное отношение

“не хуже”: (у i1 , у i2 , … у iq ,) ≥ (у j1 , у j2 , … у jq ,).

Таким образом, одно решение предпочтительнее другого, если все значения рангов первого решения не хуже значений соответствующих рангов второго решения и, по крайней мере, для одного критерия имеет место строгое предпочтение.

Будем сравнивать решения попарно. Сравниваем ранги решений Y 1 и Y 2 . Первое решение будет предпочтительнее второго, так как его ранги выше, а шестой ранг не хуже чем у второго. Второе решение исключается из дальнейшего рассмотрения.

Затем сравниваем Y 1 и Y 3 . Все ранги первого решения выше, чем у третьего, но второй ранг хуже и поэтому третье решение исключить из рассмотрения нельзя.

Сравнивая попарно остальные решения, приходим к выводу, что все они хуже, чем решения Y 1 и Y3 . Все они исключаются из дальнейшего рассмотрения. Таким образом, область допустимых решений сужена до двух эффективных решений Y 1 и Y 3 .

Определение единственного решения – заключительный этап процедуры выбора. Для решения задачи нужна дополнительная информация. Если такой информации нет, то решение можно выбрать из области эффективных решений волевым порядком. Волевое решение

будет близко к оптимальному. Дополнительная информация может быть подготовлена группой

экспертов, которые могут установить вес ωj для каждого выбранного критерия. Вес критерия назначают в пределах 0…1 (1 – существенная значимость критерия; 0,5 умеренная значимость; 0 – несущественная значимость).

Поиск минимума функций.

Для поиска минимума необходимо определить интервал, на котором функция могла бы иметь минимум. Для этого можно использовать (1) графическое представление функции, (2) аналитический анализ аппроксимирующей функции и (3) сведения о математической модели исследуемого процесса (т.е. законы поведения данной функции).

Численные методы поиска минимума функции одной переменной.

Функция f(x) имеет локальный минимум при некотором  , если существует некоторая конечная ξ-окрестность этого элемента, в которой   ,  . Требуется, чтобы на множестве X функция f(x) была по крайней мере кусочно-непрерывной.

Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение.

Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f(x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам.

Методы поиска минимума по нахождению корней уравнений.

Если функция f(x) аналитически дифференцируема, то решаем f ^/>(x) = 0

При этом условие f ^//(x) > 0 в найденной точке указывает нам на минимум. Для использования этих методов необходимо знать либо аналитический вид первой и второй производных, либо рассчитать их численно, если это не приведет к потере точности.

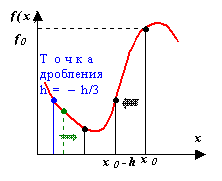
Метод дробления.

Наиболее простой метод поиска минимума. Пусть дана начальная точка x₀, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f(x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f(x_k+1) > f(x_k), где k– порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h/3 и процесс продолжается до тех пор, пока

|x_k+1 – x_k| ≤ ξ . (1)

Данный метод является одним из самых медленных для поиска минимума. Основное достоинство данного алгоритма – возможность использования в программах управления экспериментальными исследованиями, когда значения функции f(x) последовательно измеряются с шагом h ≥ h_min.

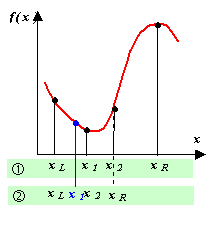
Метод золотого сечения.

Пусть f(x) задана и кусочно-непрерывна на [x_L, x_R], и имеет на этом отрезке только один локальный минимум. Золотое сечение, о котором упоминал ещё Евклид, состоит в разбиении интервала [_L, x_R] точкой x₁ на две части таким образом, что отношение длины всего отрезка к его большей части равно отношению большей части к меньшей:

Таким образом, возьмем на отрезке две точки x₁ и x₂, симметрично относительно границ делящие исходный отрезок в отношении золотого сечения:

,

,

где коэффициент  .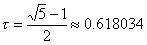

Если f(x)₁ < f(x)₂, мы должны сузить отрезок справа, т.е. новое значение _R = x₂, в противном случае x_L = x₁. Оставшаяся внутри нового отрезка точка является первым приближением к минимуму и делит этот отрезок в отношении золотого сечения. Таким образом, на каждой итерации приближения к минимуму (см. рисунок) нам нужно ставить только одну точку (x₁ или x₂), в которой считать значение функции и сравнивать его с предыдущим. Условием выхода из итерационного процесса будет, подобно предыдущему случаю, условие |x₂ – x₁| ≤ ξ.

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

Метод парабол.

Пусть f(x) имеет первую и вторую производную. Разложим f(x) в ряд Тейлора в некоторой точке x_k, ограничиваясь при этом тремя членами разложения:

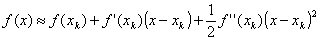
Иными словами, аппроксимируем нашу функцию в точке x_k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3):  . Пусть минимум аппроксимирующей параболы находится в точке x_k+1. Тогда вычислив значение функции f(x_k+1), мы получаем новую точку приближения к минимуму.

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f(x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагомh:

Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x_k+h, x_k, x_k–h. Окончательное выражение, по которому можно строить итерационный процесс, таково:

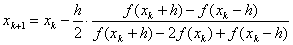. (4)

Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний ~h², сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если

1. знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагаю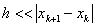т  . Иногда ради упрощения расчетов полагают  , однако это существенно уменьшает скорость сходимости.

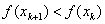2. . Если это не так, то от x_k следует сделать шаг 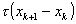 с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

В этом разделе будем рассматривать методы, используемые при поиске безусловных минимумов функций нескольких переменных.

Многомерная задача оптимизации формулируется следующим образом:

f(x)min, x Rⁿ, Rⁿ-n-мерное пространство

(т.е. ограничения на х отсутствуют),

где х=(x₁, x₂,…, x_n)^T – вектор управляемых переменных размерностью n, f - скалярная целевая функция.

Точка х является точкой глобального минимума, если для всех x Rⁿ, выполняется неравенство: f = f(x)-f(x)0 (1).

Точку глобального минимума будем обозначать х**.

Если формула (1) справедлива лишь в некоторой -окрестности точки х, т.е. для всех х, таких, что ||x-x||<, при заданном >0, то х есть точка локального минимума. Ее будем обозначать х*. Норма (модуль, длина) вектора

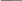||x||=(x, x)=x^T x=x₁² + x₂² + … +x_n²

(x, x)=x^T x – скалярное произведение х на себя x^T = (x₁, x₂, …, x_n)

Если же выполняется f = f(x) - f(x)  0, (2)

то х есть точка максимума (локального или глобального в соответствии с данными ранее определениями).

Исключение знака равенства из формул (1) и (2) позволяет определить точку строгого минимума или максимума.

В случае, когда f принимает как положительные и отрицательные, так и нулевые значения в зависимости от выбора точек из  - окрестности, точка х представляет собой седловую точку.

Точка х, в которой находится минимум или максимум, или седловая точка, должна удовлетворять условию стационарности:

f(x) = 0 (x – стационарная точка)

f f f ^T

f(x) = x₁, x₂, …, x_n - градиент функции f(x) = f(x₁, x₂, …, x_n)

Приведем некоторые сведения из линейной алгебры.

Квадратичной формой называется функция n переменных вида:

A(x₁, x₂, …, x_n) = A(x) = _i=1ⁿ_j=1ⁿ q_ijx_ix_j = x^TQx, где

x

x = x , Q_(n*n) = [q_ij] – матрица.

…

x

Q будем считать симметрической матрицей.

Определения:

1. матрица Q является положительно определенной тогда и только тогда, когда x^TQx > 0 для всех х  0.

2. матрица Q является положительно полуопределенной тогда и только тогда, когда значения квадратичной формы x^TQz  0, для всех х и существует вектор х  0 такой, что x^TQz = 0.

3. матрица Q является отрицательно определенной тогда и только тогда, когда -Q есть положительно определенная матрица. Другими словами – тогда и только тогда, когда x^TQx < 0 для всех х  0.

4. матрица Q является отрицательно полуопределенной тогда и только тогда, когда -Q есть положительно полуопределенная матрица.

5. матрица Q является неопределенной, если квадратичная форма x^TQx может принимать как положительные, так и отрицательные значения.

Справедливы следующие утверждения:

1) Стационарная точка х есть точка минимума, если H_f(x) = ²f(x) - положительно полуопределенная матрица.

H_f(x) = ²f(x) = [²f/(x_ix_j)] – матрица Гессе (гессиан)

2) Стационарная точка х есть точка максимума, если H_f(x) = ²f(x) - отрицательно полуопределенная матрица.

1. Стационарная точка х есть седловая точка, если H_f(x) = ²f(x) - неопределенная матрица.

Необходимые условия: для наличия в точке х* локального минимума необходимо, чтобы выполнялось равенство:

f(x*) = 0 (чтобы точка х* была стационарной)

и матрица H_f(x*) = ²f(x*) была положительно полуопределенной. (неотрицательно определенной) H_f(x) = ²f(x) = [²f/(x_ix_j)] – матрица Гессе (гессиан).

Достаточные условия: Если f(x*) = 0 и матрица H_f(x*) = ²f(x*) – положительно определена, то х* точка изолированного (строгого) локального минимума функции f(x).

Примечание. Если удастся показать, что x^T²f(x)  0 для всех х, то f(x) является выпуклой функцией, а локальный минимум оказывается глобальным.

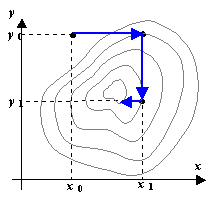
Метод координатного спуска.

Пусть требуется найти минимум f(x, y). Выберем нулевое приближение (x₀ , y₀). Рассмотрим функцию одной переменной f(x, y₀) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x₁ , y₀). Теперь точно так же будем искать минимум функции одной переменной f(x₁ , y). Этот минимум окажется в точке (x₁ , y₁). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие  .

Сходимость метода зависит от вида функции и выбора нулевого приближения. Вблизи невырожденного минимума гладкой функции спуск по координатам линейно сходится к минимуму. Если линии уровня образуют истинный овраг, возможен случай, когда спуск по одной координате приводит на дно оврага, а любое движение по следующей координате ведет на подъем. Процесс координатного спуска в данном случае не сходится к минимуму. При попадании траектории спуска в разрешимый овраг сходимость становится чрезвычайно медленной. В физических задачах овражный рельеф указывает на то, что не учтена какая-то закономерность, определяющая связь между переменными. Явный учет этой закономерности облегчает использование численных методов.

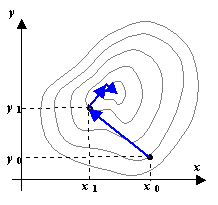
Метод градиентного (наискорейшего) спуска.

В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном  . Вдоль этого направления функция зависит от одной параметрической переменной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения  против градиента до минимума t определяет новую точку  , в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет  .

С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

9. Методы исследования операций (прямые и обратные задачи исследования операций; методы математического программирования; методы стохастического программирования; методы линейного программирования – производственные и распределительные задачи; принятие решений группой лиц).

Исследование операций — это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (или оптимального) управления организационными системами.

Предмет исследования операций — это системы организационного управления (организации), которые состоят из большого числа взаимодействующих между собой подразделений, причем интересы подразделений не всегда согласуются между собой и могут быть противоположными.

Целью исследования операций является количественное обоснование принимаемых решений по управлению организациями.

Решение, которое оказывается наиболее выгодным для всей организации, называется оптимальным, а решение, наиболее выгодное одному или нескольким подразделениям, будет субоптимальным.

Создание АСУ невозможно без предварительного обследования управляемого процесса методами математического моделирования. С ростом масштабов и сложности операций математические методы обоснования решений приобретают все большую роль. Природа систем, фигурирующих в приведенном определении под именем организационных, может быть самой различной, а их общие математические модели находят применение не только при решении производственных и экономических задач, но и в биологии, социологических исследованиях, в геологоразведке и других практических сферах.

Несмотря на многообразие задач организационного управления, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое операциональное исследование.

Задачи исследования операций делятся на две категории: а) прямые и б) обратные.

Прямые задачи отвечают на вопрос: чему будет равен показатель эффективности Z, если в заданных условиях y Î Y будет принято некоторое решение x Î X. Для решения такой задачи строится математическая модель, позволяющая выразить показатель эффективности через заданные условия и решение, а именно:

где заданные факторы (исходные данные),

управляющие переменные (решение),

Z — показатель эффективности (целевая функция),

F — функциональная зависимость между переменными.

Эта зависимость в разных моделях выражается по-разному. Зависимость между  и  обычно выражается в виде ограничений на

Если вид зависимости F известен, то показатель Z находится прямой подстановкой  и  в данный функционал.

Обратные задачи отвечают на вопрос: как при данных условиях  выбрать решение  чтобы показатель эффективности Zобратился в максимум (минимум). Такую задачу называют задачей оптимизации решения.

Пусть прямая задача решена, т.е. модель операции задана и вид зависимости F известен. Тогда обратная задача (т.е. задача оптимизации) может быть сформулирована следующим образом.

Требуется найти такое решение  при котором показатель эффективности Z = opt:

Эта формула читается так: Z есть оптимальное значение  взятое по всем решениям, входящим в множество возможных решений X.

Метод поиска экстремума показателя эффективности Z и связанного с ним оптимального решения  должен всегда выбираться, исходя из особенностей функции F и вида ограничений, накладываемых на решение. (Например, классическая задача линейного программирования.)

Математическое программирование (оптимальное программирование) — область прикладной математики, объединяющая различные математические методы и дисциплины: линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование и др. Общая задача математического программирования состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений. В самом общем виде эта задача записывается так:

где — совокупность управляющих воздействий; М — область допустимых значений переменных; G — целевая функция.

Названные выше разнообразные дисциплины отличаются Друг от друга видом целевой функции G(m) и области М. Например, если G(m) и М — линейны, имеем задачу линейного программирования; если же дополнительно ставится условие, чтобы переменные были целочисленны — задача целочисленного программирования; если зависимость (т. е. форма G(m)) носит нелинейный характер — задача нелинейного программирования и т. д.

Проблематика оптимизации решений имеет давнюю историю и восходит к задачам поиска экстремума в математическом анализе и вариационном исчислении.

К математическому программированию относится:

1. Линейное программирование: состоит в нахождении экстремального значения линейной функции многих переменных при наличии линейных ограничений, связывающих эти переменные; 

2. Нелинейное программирование: целевая функция и ограничения могут быть нелинейными функциями; 

3. Особым случаем в задачах линейного и нелинейного программирования является случай, когда на оптимальные решения накладывается условие целочисленности. Такие задачи относятся к целочисленному программированию;

4. Динамическое программирование: для отыскания оптимального решения планируемая операция разбивается на ряд шагов (этапов) и планирование осуществляется последовательно от этапа к этапу. Однако выбор метода решения на каждом этапе производится с учетом интересов операции в целом; 

5. Теория графов: с помощью теории графов решаются многие сетевые задачи, связанные с минимальным протяжением сети, построение кольцевого маршрута и т.д. 

6. Стохастическое линейное программирование  Бывает много практических ситуаций, когда коэффициенты c_i целевой функции, коэффициенты a_ij в матрице коэффициентов, коэффициенты ограничений b_i - являются случайными величинами. В этом случае сама целевая функция становится случайной величиной, и ограничения типа неравенств могут выполняться лишь с некоторой вероятностью. Приходится менять постановку самих задач с учётом этих эффектов и разрабатывать совершенно новые методы их решения. Соответствующий раздел получил название стохастического программирования. 

7. Геометрическое программирование Под задачами геометрического программирования понимают задачи наиболее плотного расположения некоторых объектов в заданной двумерной или трехмерной области. Такие задачи встречаются в задачах раскроя материала для производства каких-то изделий и т.п. Это - еще недостаточно разработанная область математического программирования и имеющиеся здесь алгоритмы в основном ориентированы на сокращение перебора вариантов с поиском локальных минимумов. 

8. Задачами теории массового обслуживания является анализ и исследование явлений, возникающих в системах обслуживания. Одна из основных задач теории заключается в определении таких характеристик системы, которые обеспечивают заданное качество функционирования, например, минимум времени ожидания, минимум средней длины очереди. 

9. Теория игр пытается математически объяснить явления возникающие в конфликтных ситуациях, в условиях столкновения сторон. Такие ситуации изучаются психологией, политологией, социологией, экономикой. 

Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:

• математические модели очень большого числа экономических задач линейны относительно искомых переменных;

• эти типы задач в настоящее время наиболее изучены;

• для них разработаны специальные конечные методы, с помощью которых эти задачи решаются, и соответствующие стандартные программы для их решения на ЭВМ;

• многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;

• некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что  а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

• максимум или минимум целевой функции (критерий оптимальности);

• систему ограничений в форме линейных уравнений и неравенств;

• требование неотрицательности переменных.

В других ситуациях могут возникать задачи с большим количеством переменных, в систему ограничений которых, кроме неравенств, могут входить и равенства. Поyтому в наиболее общей форме задачу линейного программирования формулируют следующим образом:

	(2.4)
	(2.5)
	(2.6)

Коэффициенты a_i,j, b_i, c_j, j = 1, 2, ... , n, i =1, 2, ... , m – любые действительные числа (возможно 0).

Итак, решения, удовлетворяющие системе ограничений (2.4) условий задачи и требованиям неотрицательности (2.5), называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) (2.6) целевой функции, - оптимальными.

Выше описанная задача линейного программирования (ЗЛП) представлена в общей форме, но одна и та же (ЗЛП) может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная.

В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, ..., х_n являются неотрицательными:

	(2.7)
	(2.8)
	(2.9)

К канонической форме можно преобразовать любую задачу линейного программирования.

Правило приведения ЗЛП к каноническому виду:

1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» - со знаком «-»

(2.10)

Вводим переменную

.

Тогда неравенство (2.10) запишется в виде:

(2.11)

В каждое из неравенств вводится своя “уравнивающая” переменная, после чего система ограничений становится системой уравнений.

2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных

, l - свободный индекс

3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1)

4. Наконец, если исходная задача была задачей на минимум, то введением новой целевой функции F₁ = -F мы преобразуем нашу задачу на минимум функции F в задачу на максимум функции F₁.

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные X₁, X₂, ..., X_r. Тогда наша система уравнений может быть записана как

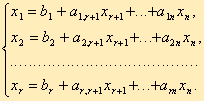
К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.

Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X₁, X₂, ..., X_r, то решение {b₁, b₂,..., b_r, 0, ..., 0} будет опорным при условии, что b₁, b₂,..., b_r ≥ 0.

Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.

Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.

Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.

Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.

Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.  При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.

Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.

Не останавливаясь подробнее на сути алгоритма, опишем его вычислительную сторону. Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные. Вопрос об этих предварительных преобразованиях мы рассмотрим ниже. Сейчас же будем считать, что они уже выполнены и задача имеет вид:

Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X₁, X₂, ..., X_r и что при этом b₁, b₂,..., b_r ≥ 0 (соответствующее базисное решение является опорным).

Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств:

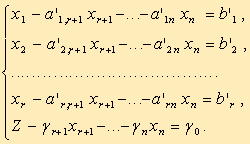
Далее эта система оформляется в виде симплекс-таблиц:

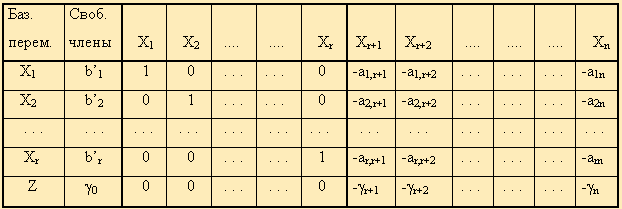
Примечание. Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими.

Порядок работы с симплекс таблицей

Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.

Алгоритм перехода к следующей таблице такой:

• просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов 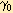 ) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;

• просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;

• среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находитсяключевой;

• в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:

• разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.

• строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.

• в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1.

• столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же.

• строка, у которой в ключевом столбце имеется 0,в новой таблице будет такой же.

• в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы:

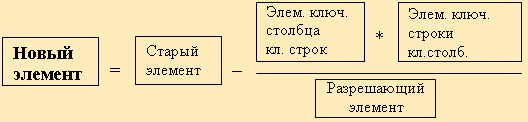
В результате получают новую симплекс-таблицу, отвечающую новому базисному решению.

Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте   (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму. 

Частным случаем задачи линейного программирования является транспортная задача.  ТЗ в общем виде состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А₁ , А₂ , ..., А_m в n пунктов назначения B₁ , B₂ , ..., B_n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки.  Рассмотрим задачу с первым критерием, обозначив через сn тарифы перевозок единицы груза из i-го пункта отправления в j-й пункт назначения, через a_i - запасы груза в пункте А_i через b_j - потребности в грузе пункта B_j , x_ij - количество единиц груза, перевозимого из i-го пункта в j-й пункт.  Составим математическую модель задачи. Так как от i-гo поставщика к j-му потребителю запланировано к перевозке x_ij единиц груза.

Таблица 2.2

Поставщики	Потребители				Запасы
	B1	B2	...	Bn
А1	C11 X11	C12 X12	...	C1n X1n		a1
А2	C21 X21	C22 X22	...	C2n X2n		a2
...	...	...	...	...		...
Аm	Cm1 Xm1	Cm2 Xm2	...	Cmn Xmn		am
Потребности	b1	b2	...	bn		∑ai=∑bj

Соответственно математическая постановка задачи состоит в определении минимума целевой функции

(2.17)

при условиях:

	(i = l, ..., m),	(2.18)
	(j = 1, ..., n),	(2.19)
xij ≥ 0	(i = l, ..., m; j = l, ..., n).	(2.20)

Всякое неотрицательное решение систем уравнений (2.18)-(2.20), определяемое матрицей X=(x_ij ), называют опорным планом ТЗ, а план X*=(x_ij ), при котором функция Z принимает минимальное значение - называется оптимальным планом ТЗ.  Все данные, а затем и опорный план, удобно занести в распределительную таблицу (см, в примерах параграфа).  Если общее количество груза в пунктах отправления и общая потребность в нем в пунктах назначения совпадают, т.е.

(2.21)

то модель ТЗ называется закрытой.

Метод северо-западного угла

Пусть условия транспортной задачи заданы таблице 2.3. Не учитывая стоимости перевозки единицы груза, начинаем удовлетворение потребностей первого потребителя B1 за счет запаса поставщика А₁. Для этого сравниваем a₁ = 100 с b_i = 200, a₁< b₁ меньший из объемов, т. е. = 100 ед. записываем в левый нижний угол клетки А₁B₁. Запасы первого поставщика полностью израсходованы, по этому остальные клетки первой строки прочеркиваем. Потребности В остались неудовлетворенными на 200–100=100 ед. Сравниваем этот остаток с запасами поставщика А₂: так как 100<250, то 100 ед. записываем в клетку А₂ .B₁, чем полностью удовлетворяем потребности потребителя B₁, а оставшиеся клетки в первом столбце прочеркиваем.

Таблица 2.3

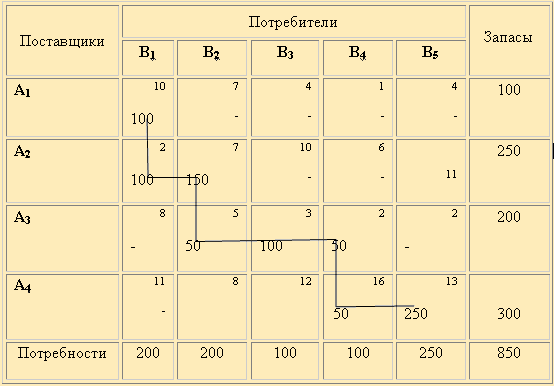
У поставщика А₂ осталось 150 ед. груза. Удовлетворяем потребителя B₂ за счет оставшегося у поставщика А₂ груза. Для этого сравниваем этот остаток с потребностями потребителя B₂: 150<200, записываем 150 ед. в клетку А₂B₂ и, так как запасы А₂ полностью израсходованы, прочеркиваем остальные клетки второй строки. Потребности B₂ остались неудовлетворенными на 50 ед. Удовлетворяем их за счет поставщика А₃ и переходим к удовлетворению B₃ за счет остатка, имеющегося у поставщика А₃, и т. д. Процесс продолжаем до тех пор, пока не удовлетворим всех потребителей за счет запасов поставщиков. На этом построение первоначального опорного плана заканчивается. Таким образом, в табл. в правых верхних углах клеток стоят числа, определяющие стоимость перевозки единицы грузов, а в левых нижних углах — числа, определяющие план перевозок, так как их сумма по строкам равна запасам соответствующего поставщика, а сумма по столбцам — потребности соответствующего потребителя.  Проверим, является ли план, построенный в табл. 2.2, опорным. Видим, что, начиная движение от занятой клетки A1B1, вернуться не только в нее, но и в любую другую занятую клетку, двигаясь только по занятым ячейкам, невозможно. Следовательно, план является опорным. В то же время план невырожденный, так как содержит точно m + n -1 = 4 + 5 - 1 = 8 занятых клеток.  При составлении первоначального опорного плана методом северо-западного угла стоимость перевозки единицы груза не учитывалась, поэтому построенный план далек от оптимального, получение которого связано с большим объемом вычислительных работ. Поэтому рассмотренный метод используется при вычислениях-с помощью ЭВМ.  Найдем общую стоимость составленного плана как сумму произведений объемов перевозок, стоящих в левом углу занятых клеток, на соответствующие стоимости в этих же ячейках:  Z = 100 *10 + 100*2 + 150 *7+ 50 *5 + 100*3 + 50*2 + 50*16+ 250*13 = 6950 (eд. стоимости)  Если при составлении опорного плана учитывать стоимость перевозки единицы груза, то, очевидно, план будет значительно ближе к оптимальному.

Метод минимальной стоимости

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j . Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.  Составим с помощью этого метода опорный план уже рассмотренной задачи. Запишем ее условие в таблицу (табл. 2.5). Выбираем в таблице наименьшую стоимость (это стоимость, помещенная в клетке A₁ , B₄ ) так как A₁ = b₄, 100 ед. груза помещаем в этой клетке и исключаем из рассмотрения первую строку и четвертый столбец. В оставшейся таблице стоимостей наименьшей является стоимость, расположенная в клетке A₂ , B₁ и в клетке A₃ , B₅. Заполняем любую из них, например A₂ , B₁. Имеем 200 < 250, следовательно, записываем в нее 200 и исключаем из рассмотрения столбец B₁. В клетку A₃ , B₅ записываем 200ед. и исключаем из рассмотрения строку A₃ . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план  X = (X₁₄ = 100; X₂₁ = 200; X₂₂ = 50; X₃₅= 200, X₄₂ = 150; X₄₃ = 100; X₄₅ = 50),  остальные значения переменных равны нулю.

Таблица 2.5

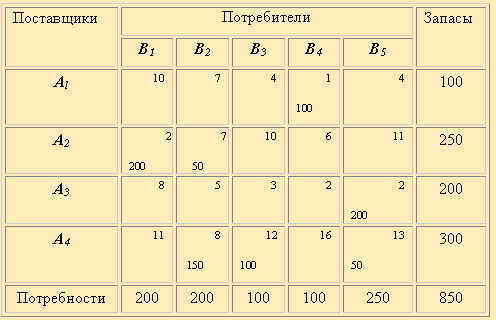
План не содержит циклов и состоит из семи положительных перевозок, следовательно, является вырожденным опорным планом. Определим его стоимость:  Z = 100*1+200*2+50*7+200*2+150*8+100*12+50*13= 4300 (ед)  Стоимость плана перевозок значительно меньше, следовательно, он ближе к оптимальному.

Метод потенциалов

Пусть одним из рассмотренных в п.2.6 методов найден опорный план, содержащий n + m - 1 занятых клеток (в некоторых из них могут стоять нули). Поставим в соответствие каждому пункту отправления А_i некоторое число u_i (i = l, ..., m) и каждому пункту назначения B_j - число v_j (j = 1, ..., n). Эти числа назовем потенциалами, соответственно, пунктов отправления и пунктов назначения.

Вопрос об оптимальности опорного плана решает следующая теорема:

Теорема 5. Если для некоторого плана X*= (x_ij ), (i = l, ..., m; j = l, ..., n) транспортной задачи выполняются условия:

1. u_i + v_j = c_ij для x_ij > 0 (для занятых клеток),          (2.22) 2. u_i + v_j < c_ij для x_ij = 0 (для свободных клеток),     (2.23)

то план X* является оптимальным. Из теоремы следует, что если для некоторой свободной клетки  u_i + v_j < c_ij , то план не является оптимальным.

Отметим, что система (2.22) (m + n - 1) уравнений содержит (m + n) неизвестных u_i , v_j , и потому, приравнивая одно из них, например u₁ к нулю, однозначно определим остальные неизвестные.

Для «улучшения» опорного плана (при невыполнении условия (2.23)) выбирают свободную клетку с max (u_i + v_j - c_ij ) и строят для нее цикл пересчета (сдвига).

Циклом называют замкнутую ломаную линию, все вершины которой лежат в занятых ячейках, кроме одной, расположенной в свободной клетке, подлежащей заполнению, а звенья параллельны строкам и столбцам, причем в каждой строке (столбце) лежит не более 2-х вершин. Всем вершинам поочередно приписывают знаки «+» и «-», начиная со свободной клетки.  Далее, в свободную клетку помещают груз величиной λ, равной минимальному значению из всех чисел в отрицательных ячейках цикла. Во все положительные клетки прибавляется λ, из отрицательных - вычитается λ (сдвиг по циклу). Нетрудно подсчитать, насколько изменится (уменьшится) стоимость перевозок при новом плане:

, где   - сумма тарифов в положительных вершинах,  - в отрицательных вершинах цикла.  Новый опорный план снова проверяют на оптимальность с помощью системы уравнений потенциалов.  Заметим, что в результате пересчета по циклу может оказаться число занятых клеток меньше, чем n+m-1 (план называется вырожденным). В этом случае следует заполнить числом «0» пустую клетку, имеющую минимальный тариф, и не образующую с занятыми клетками замкнутого прямоугольного контура.

Свойство 1. Если, для некоторого оптимального плана X*= (x_ij ), (i = l, ..., m; j = l, ..., n) транспортной задачи, выполняется условие: u_i + v_j = c_ij для x_ij =0 (для свободных клеток), то, существует как минимум еще один оптимальный план, для которого общая стоимость плана перевозок остается прежней, поскольку (u_i+ v_j) – c_ij = 0.

Свойство 2. Любая выпуклая линейная комбинация двух оптимальных планов также является оптимальным планом.  Это свойство можно использовать для улучшения планирования, при этом можно учесть особенности, которые не были учтены в математической модели задачи (ранее взятые договорные обязательства, сложившиеся традиции в отношениях и т. д.).

Стохасти́ческое программи́рование — это подход, позволяющий учитывать неопределённость в оптимизационных моделях.

В то время как детерминированные задачи оптимизации формулируются с использованием заданных параметров, реальные прикладные задачи обычно содержат некоторые неизвестные параметры. Когда параметры известны только в пределах определенных границ, один подход к решению таких проблем называется робастной оптимизацией. Этот подход состоит в том, чтобы найти решение, которое является допустимым для всех таких данных и в некотором смысле оптимально.

Модели стохастического программирования имеют подобный вид, но используют знание распределений вероятностей для данных или их оценок. Цель здесь состоит в том, чтобы найти некоторое решение, которое является допустимым для всех (или почти всех) возможных значений данных и максимизируют математическое ожидание некоторой функции решений и случайных переменных. В общем, такие модели формулируются, решаются аналитически или численно, их результаты анализируются, чтобы обеспечить полезную информацию для лиц, принимающих решения.

Наиболее широко применяются и хорошо изучены двухэтапные линейные модели стохастического программирования. Здесь лицо, принимающее решение, предпринимает некоторое действие на первом этапе, после которого происходит случайное событие, оказывающее влияние на результат решения первого этапа. На втором этапе может тогда быть принято корректирующее решение, которое компенсирует любые нежелательные эффекты в результате решения первого этапа.

Оптимальным решением такой модели является единственное решение первого этапа и множество корректирующих решений (решающих правил), определяющих, какое действие должно быть предпринято на втором этапе в ответ на каждый случайный результат.

Процесс принятия группового решения тесно связан с проблемой лидерства и руководства, потому что принятие решения – одна из важных функций руководителя, а организация группы для принятия такого решения – особенно сложная функция. В современных условиях, когда деятельность групп активизируется во многих звеньях общественного организма, эта проблема приобретает особую актуальность. Не только в социальной психологии, психологии управления, но и в повседневной практике разработаны различные методы принятия групповых решений, и дело науки – выявить в полной мере их возможности, оценить их эффективность и применимость в различных конкретных ситуациях. Более подробное рассмотрение управленческих аспектов процесса принятия группового решения будет способствовать повышению качества групповых решений и сплоченности коллективов, более эффективной деятельности групп.

При групповом принятии решения речь идет о групповом обсуждении определенной проблемы, в результате, которого группа как таковая принимает конкретное решение.

Процесс группового принятия решения состоит из четырех этапов:

1. Установление фактов (групповое интервью).

2. Оценка фактов (мнения по поводу установленных фактов).

3. Поиск решения (брейнсторминг).

4. Принятие решений.

Первый этап: основная задача заключается в сборе данных. Этот этап носит исключительно фактический и объективный характер. На этом этапе участники совместного обсуждения стараются воздерживаться от оценки собираемых фактов. Наиболее распространенный метод сбора всей совокупности мнений в группе по определенному вопросу – групповое интервью. Эффективность проведения группового интервью зависит от тщательности подготовки:

• заранее оповестить всех членов группы о целях группового обсуждения, четко обозначить тему;

• выбрать удобное для всех время обсуждения, установив продолжительность около 1,5 часов;

• обеспечить физический и психологический комфорт (желательно иметь круглый стол, должны отсутствовать посторонние наблюдатели и т.д.).

Примером коллективного принятия решений может служить метод Дельфи, получивший название от греческого города Дельфы, прославившегося жившими там мудрецами — предсказателями будущего. Метод Дельфи — многотуровая процедура анкетирования. После каждого тура данные анкетирования дорабатываются, и полученные результаты сообщаются экспертам с указанием расположения оценок. Первый тур анкетирования проводится без аргументации, во втором отличающийся от других ответ подлежит аргументации или же эксперт может изменить оценку. После стабилизации оценок опрос прекращается и принимается предложенное экспертами или скорректированное решение.

Морфологический метод и метод анализа круга проблем. Методы состоят в разложении исходной проблемы на компоненты или возникающие проблемы, а затем в их последующей разбивке на альтернативные способы реализации. Затем составляются все возможные варианты сочетаний. Для каждого из них или лишь для наиболее перспективных вариантов составляется соответствующий проект .

Метод аналогий. Идея метода состоит в вычленении возникшей проблемы и попытке ее решения с помощью идей из других сфер жизни и науки. Одно время метод применялся настолько успешно, что на его основе родилась целая наука - синектика. Ее область, занимающаяся заимствованием технических идей в биологии, называется бионикой.

Для использования метода аналогий необходимо:

• вычленить причину затруднений;

• предельно формализовать ее до уровня, воспринимаемого специалистами из других областей;

• описать цели будущего решения и объективные ограничения;

• выделить область жизни или науки, в которой могут быть близкие по своему смыслу решения;

• подобрать команду специалистов из выбранной области;

• организовать и провести мозговой штурм;

• интерпретировать для исходной области полученные варианты решений;

• выбрать из них реализуемые и наиболее эффективные¹.

Случайный импульс. Наш мыслительный аппарат функционирует в виде самоукрупняющейся запоминающей системы. Объем внимания отличается ограниченностью и ассоциативностью. Т.е. при одновременном поступлении в мозг двух сигналов при специально созданных условиях между ними должна установиться некая логическая цепочка, которая может существенно изменить восприятия каждого из сигналов.

Основные приемы для ускорения этого процесса:

• объединение множества людей;

• посещение мест, где много случайных вещей (магазин, выставка, библиотека и т.д.);

• сознательное объединение ранее несвязанных мыслей, например, с помощью случайных слов-подсказок².

Метод «635». Шесть человек высказывают по три идеи по заданному вопросу за пять минут. Затем по часовой стрелке листки с их мнениями передаются, например, по часовой стрелке. За следующие пять минут каждый участник должен ознакомиться со всеми предложениями своего соседа и детализировать их. Так поступают до тех пор, пока каждый не поработал над всеми идеями группы. Через полчаса, как максимум, готово 18 разработанных предложений. Следующие полчаса даются на их обсуждение, дополнение и выбор наилучших вариантов³.

Метод модераций. Участники заполняют по три карточки с кратким описанием имеющихся проблем (анонимно). Модератор тасует полученные карточки и по очереди оглашает их содержание, предлагая отнести их к определенным группам. Если мнения участников расходятся, окончательное решение принадлежит автору данной карточки. В результате все проблемы оказываются разбиты на группы (кластеры). Обсуждается каждый из кластеров. Предлагаются следующие возможности: исключение (включение) из него каких-либо проблем, разбиение на несколько более мелких групп или, наоборот, их укрупнение. Разрабатывается общее наименование кластеров. Определяется их относительная важность.

Есть еще японская (кольцевая) система принятия решений — «кингисё», суть которой состоит в том, что на рассмотрение готовится проект новшества. Он передается для обсуждения лицам по списку, составленному руководителем. Каждый должен рассмотреть предлагаемое решение и дать свои замечания в письменном виде. После этого проводится совещание. Как правило, приглашаются те специалисты, чье мнение руководителю не совсем ясно. Эксперты выбирают свое решение в соответствии с индивидуальными предпочтениями. И если они не совпадают, то возникает вектор предпочтений, который определяют с помощью одного из следующих принципов:

• большинства голосов — выбирается решение, имеющее наибольшее число сторонников;

• диктатора — за основу берется мнение одного лица. Этот принцип характерен для военных организаций, а так же для принятия решений в чрезвычайных обстоятельствах;

• принцип Курно используется в том случае, когда коалиций нет, т.е. предлагается число решений, равное числу экспертов. В этом случае необходимо найти такое решение, которое отвечало бы требованию индивидуальной рациональности без ущемления интересов каждого в отдельности;

• принцип Парето используется при принятии решений, когда все эксперты образуют единое целое, одну коалицию. В этом случае оптимальным будет такое решение, которое невыгодно менять сразу всем членам группы, поскольку оно объединяет их в достижении общей цели;

• принцип Эджворта используется в том случае, если группа состоит из нескольких коалиций, каждой из которых невыгодно отменять свое решение⁴.

Зная предпочтения коалиций, можно принять оптимальное решение, не нанося ущерба друг другу.

Интересные результаты были получены Д. Снайзек, которая сопоставляла пять типов методик принятия решений, применяемых группами:

1) «консенсус», когда в лобовом, открытом обсуждении выбирается оценка, принимаемая всеми членами группы;

2) «диалектическая» методика, в которой члены группы обсуждали факторы, которые могут повлиять на их оценку;

3) «диктатура», когда обсуждение заканчивается выбором субъекта, чья оценка и станет оценкой группы;

4) метод Дельфи, когда члены группы не встречаются лицом к лицу, а представляют ответы анонимно в серии раундов, пока не будет достигнут консенсус или принято среднее решение;

5) «коллективная» методика, предотвращает все интриги среди членов группы, просто усредняя индивидуальные оценки для получения оценки коллективной⁵.

Автор обнаружил, что каждая из четырех первых методик достигала более точных результатов, чем простое усреднение (пятая методика), но лучшие результаты принесла «диктатура», при которой процент ошибок был в три раза меньше. Характерно, что в каждом случае применения метода «диктатуры», «диктатор» группы изменял свое конечное мнение в направлении коллективного среднего, тем самым увеличивая величину ошибки. Другими словами, группы были способны выбирать «диктаторов», но они под воздействием феномена «огруппления мышления» и других факторов группового давления, быстро становились «демократами» и тем самым снижали эффективность групповой работы. Результаты данного исследования еще раз обращают внимание на то, что при решении дилеммы: «Лучше одна голова или несколько голов?», следует учитывать, как эти головы соединены и взаимодействуют.

Действительно, добиться высокой эффективности при организации групповой деятельности не легко. Слишком много факторов психологических, социальных, этно-функциональных… и даже пространственно-территориальных влияет на успешность каждого участника совместной деятельности и всей группы в целом.

!!!10 вопрос отсутствует в билетах!!!
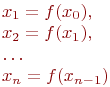
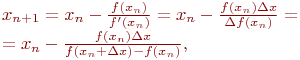
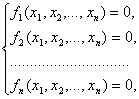
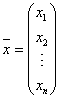