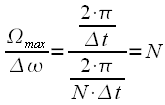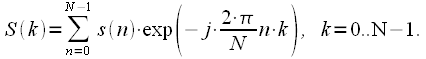- •Основы информационных технологий (теория систем, дискретная и компьютерная математика, теория управления, моделирование) (Первые вопросы в билетах).
- •Интерполирование функций (многочленами Лагранжа; интерполяционная формула Ньютона; интерполяция кубическими сплайнами).
- •Приближение функций (метод наименьших квадратов; линейная регрессия; нелинейная регрессия; полиномиальная аппроксимация; дискретное преобразование Фурье).
- •Формула трапеций
- •Численное решение систем линейных алгебраических уравнений (метод Гаусса; метод итераций).
- •11. Универсальный метод информационных технологий – статистическое моделирование нелинейных систем со случайными характеристиками в условиях помех (метод Монте-Карло).
- •!!!13 И 14 вопросы отсутствуют в билетах!!!
- •!!!16 Вопрос отсутствует в билетах!!!
- •1.2.1. Принцип разомкнутого управления
- •1.2.2. Принцип компенсации
- •1.2.3. Принцип обратной связи
- •1. Введение
- •2. Итерационные методы Якоби и Зейделя
- •3. Метод последовательной верхней релаксации
- •4. Матрично-векторное представление итерационных методов
- •Динамические модели в экономике (регрессионные, авторегрессионные, регрессионно-авторегрессионные модели; модели накопления и дисконтирования; модели «затраты-выпуск»).
- •Основы вычислительной техники. (Вторые вопросы в билетах)
- •Характеристики современных операционных систем (многопоточность, симметричная многопроцессорность, распределенные операционные системы, объектно-ориентированный дизайн).
- •Дискретный сигнал
- •Вычислительные сети и системы (протоколы обмена тср, iр, ssl, skip, NetBeui, ipx, spx, NetBios, модель osi, типы соединения эвм, используемые при построении локальных сетей).
- •Информация (аналоговая и цифровая информация, оценки количества информации, энтропийный подход).
- •Структура микропроцессора (алу, регистры: аккумуляторы, ввода-вывода, понятие шины: шина данных, адресная шина, шина команд; запоминающие устройства: пзу, озу, созу, кэш-память).
- •!!!16 Вопроса нет в билетах!!!
- •17. Понятие нелинейных преобразователей (транзисторы, ключи, диодные выпрямители, логические элементы, нейронные сети).
- •1.8. Основные методы расчета сложных электрических цепей
- •19. Расчет комплексных сопротивлений линейных цепей (последовательные цепи: rc-цепь, rl-цепь, rlc-цепь; параллельные цепи: rc-цепь, rl-цепь, lc-цепь; последовательно-параллельные цепи: r-lc, c-rl).
- •Основы алгоритмизации и программирования. (Третьи вопросы в билетах)
- •2. Методы сортировки и поиска данных в массивах и файлах. Оценки скорости.
- •Современные языки программирования (с, Java, Delphi, vb). Типы данных языка. Структура приложения.
- •Примитивные типы
- •Типы данных
- •Объекты
- •Статическая и динамическая память, определение, область применения. Алгоритмы обработки очереди, списка, стека.
- •4 Шага добавления
- •Основные компоненты в языках (с, Java, Delphi). Их свойства, методы, события. Реализация графики.
- •7. Понятия объектно-ориентированного программирования. Поля, свойства, методы, события. Область видимости. Пример класса.
- •Базы данных. Типы бд. Реляционные бд. Типы полей. Типы связей. Язык запросов sql. Индексирование баз данных.
- •Создание Internet-приложений (на стороне клиента и сервера). Язык разметки гипертекста html. Специализированные инструменты (php). Создание Internet-приложений средствами языков с, Java, Delphi.
- •Глава 1 – содержание элемента html
- •6.3. Рисунки
- •Основные элементы блок схем программирования, типовые блок схемы (ввода-вывода, исполнения команд, условного перехода; ветвящиеся программы, циклические программы, вложенные циклы).
Приближение функций (метод наименьших квадратов; линейная регрессия; нелинейная регрессия; полиномиальная аппроксимация; дискретное преобразование Фурье).
Теория приближений — раздел математики, изучающий вопрос о возможности приближенного представления одних математических объектов другими, как правило более простой природы, а также вопросы об оценках вносимой при этом погрешности. Значительная часть теории приближения относится к приближению одних функций другими, однако есть и результаты, относящиеся к абстрактным векторным или топологическим пространствам.
Вместо вычисления точного значения функции
 при
малых
при
малых  можно
воспользоваться самим
,
то есть
можно
воспользоваться самим
,
то есть  .
Чем больше будет
,
тем больше будет погрешность такого
приближения.
.
Чем больше будет
,
тем больше будет погрешность такого
приближения.
Чтобы запомнить некоторую функцию можно запомнить ее значения в некоторых точках (говорят: на сетке), а в остальных точках вычислять ее по какой-нибудь интерполяционной формуле. Вопрос об оптимальном выборе (для конкретной функции или для функций из какого-то класса) сетки и формулы относится как раз к теории приближения.
Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.
Приближение функций – нахождение по данной функции некоторой другой, в определенном смысле мало отличающейся от данной, но обладающей, в отличие от нее, какими-то специальными требуемыми свойствами – принадлежащей к определенному семейству, семейству приближающих функций.
Часто для приближения функций используют алгебраические многочлены Рn(x) = a0xn + a1xn-1 + a2xn-2 + … + an-1x + an,
рациональные дроби
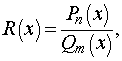
где числитель и знаменатель – алгебраические многочлены; тригонометрические полиномы

Вообще для приближения используют многочлены, составленные из заданного семейства функций fk(x):
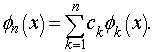
Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.
Постановка
задачи приближения функции по методу
наименьших квадратов. Пусть
функция y=f(x) задана
таблицей своих значений: ![]() , i=0,1,-n. Требуется
найти многочлен фиксированной степени m,
для которого среднеквадратичное
отклонение (СКО)
, i=0,1,-n. Требуется
найти многочлен фиксированной степени m,
для которого среднеквадратичное
отклонение (СКО)  минимально.
минимально.
Так
как многочлен ![]() определяется
своими коэффициентами, то фактически
нужно подобрать набор кофициентов
определяется
своими коэффициентами, то фактически
нужно подобрать набор кофициентов ![]() ,
минимизирующий функцию
,
минимизирующий функцию  .
.
Используя
необходимое условие
экстремума, ![]() , k=0,1,-m получаем
так называемую нормальную систему
метода наименьших квадратов:
, k=0,1,-m получаем
так называемую нормальную систему
метода наименьших квадратов: ![]() , k=0,1,-m.
, k=0,1,-m.
Полученная система есть система алгебраических уравнений относительно неизвестных . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
Запишем нормальную
систему наименьших квадратов для
двух простых случаев: m=0
и m=2.
При m=0
многочлен примет вид: ![]() .
Для нахождения неизвестного
коэффициента
.
Для нахождения неизвестного
коэффициента ![]() имеем
уравнение:
имеем
уравнение: .
Получаем, что коэффициент
.
Получаем, что коэффициент ![]() есть
среднее арифметическое значений функции
в заданных точках.
есть
среднее арифметическое значений функции
в заданных точках.
Если
же используется многочлен второй
степени ![]() ,
то нормальная система уравнений примет
вид:
,
то нормальная система уравнений примет
вид:

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x
![]()
где ![]() —
вектор неизвестных параметров модели
—
вектор неизвестных параметров модели
![]() —
случайная
ошибка модели.
—
случайная
ошибка модели.
Пусть
также имеются выборочные наблюдения
значений указанных переменных. Пусть ![]() —
номер наблюдения (
—
номер наблюдения (![]() ).
Тогда
).
Тогда ![]() —
значения переменных в
-м
наблюдении. Тогда при заданных значениях
параметров b можно рассчитать теоретические
(модельные) значения объясняемой
переменной y:
—
значения переменных в
-м
наблюдении. Тогда при заданных значениях
параметров b можно рассчитать теоретические
(модельные) значения объясняемой
переменной y:
![]()
Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):
![]()
Величина остатков зависит от значений параметров b.
Сущность
МНК (обычного, классического) заключается
в том, чтобы найти такие параметры b, при
которых сумма квадратов
остатков ![]() (англ. Residual
Sum of Squares[1])
будет минимальной:
(англ. Residual
Sum of Squares[1])
будет минимальной:
![]()
где:
![]()
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:
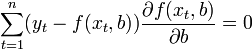
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).
Суть
метода наименьших квадратов (МНК).
Задача
заключается в нахождении коэффициентов
линейной зависимости, при которых
функция двух переменных а и b ![]() принимает
наименьшее значение. То есть, при
данных а и b сумма
квадратов отклонений экспериментальных
данных от найденной прямой будет
наименьшей. В этом вся суть метода
наименьших квадратов.
Таким
образом, решение примера сводится к
нахождению экстремума функции двух
переменных.
Вывод
формул для нахождения
коэффициентов.
Составляется
и решается система из двух уравнений с
двумя неизвестными. Находим частные
производные функции
по
переменным а и b,
приравниваем эти производные к
нулю.
принимает
наименьшее значение. То есть, при
данных а и b сумма
квадратов отклонений экспериментальных
данных от найденной прямой будет
наименьшей. В этом вся суть метода
наименьших квадратов.
Таким
образом, решение примера сводится к
нахождению экстремума функции двух
переменных.
Вывод
формул для нахождения
коэффициентов.
Составляется
и решается система из двух уравнений с
двумя неизвестными. Находим частные
производные функции
по
переменным а и b,
приравниваем эти производные к
нулю.
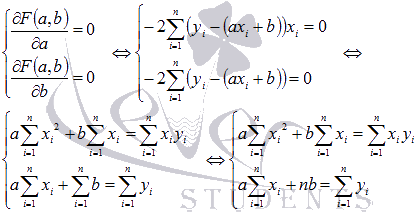 Решаем
полученную систему уравнений любым
методом (например методом
подстановки или методом
Крамера)
и получаем формулы для нахождения
коэффициентов по методу наименьших
квадратов (МНК).
Решаем
полученную систему уравнений любым
методом (например методом
подстановки или методом
Крамера)
и получаем формулы для нахождения
коэффициентов по методу наименьших
квадратов (МНК).
 При
данных а и b функция
принимает
наименьшее значение. Доказательство
этого факта приведено ниже
по тексту в конце страницы .
Вот
и весь метод наименьших квадратов.
Формула для нахождения параметра a содержит
суммы
При
данных а и b функция
принимает
наименьшее значение. Доказательство
этого факта приведено ниже
по тексту в конце страницы .
Вот
и весь метод наименьших квадратов.
Формула для нахождения параметра a содержит
суммы ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
параметр n -
количество экспериментальных данных.
Значения этих сумм рекомендуем вычислять
отдельно. Коэффициент b находится
после вычисления a.
и
параметр n -
количество экспериментальных данных.
Значения этих сумм рекомендуем вычислять
отдельно. Коэффициент b находится
после вычисления a.
Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости. Метод аппроксимации линейной зависимости между входными и выходными переменными. Если ищется связь между одной входной и одной выходной переменными, то имеет место простая линейная регрессия. Для этого определяется уравнение регрессии y=ax+b и строится соответствующая прямая, известная как линия регрессии. Коэффициенты a и b, называемые также параметрами модели, выбираются таким образом, чтобы сумма квадратов отклонений точек, соответствующих реальным наблюдениям данных, от линии регрессии, была бы минимальной. Подбор коэффициентов производится по методу наименьших квадратов. Если ищется зависимость между несколькими входными и одной выходной переменными, то имеет место множественная линейная регрессия. Соответствующее уравнение имеет вид:
Y = b0+d1x1+b2x2+...+bnxn,
где n – число входных переменных. Очевидно, что в данном случае модель будет описываться не прямой, а гиперплоскостью. Коэффициенты уравнения множественной линейной регрессии подбираются так, чтобы минимизировать сумму квадратов отклонения реальных точек данных от этой гиперплоскости. Широкое применение линейной регрессии обусловлено тем, что достаточно большое количество реальных процессов в экономике и бизнесе можно с достаточной точностью описать линейными моделями. В Data Mining регрессия широко используется для решения задач прогнозирования и численного предсказания.
Регрессионная модель
![]()
где ![]() -параметры
модели,
-
случайная ошибка модели, называется
линейной регрессией, если функция
регрессии
-параметры
модели,
-
случайная ошибка модели, называется
линейной регрессией, если функция
регрессии ![]() имеет
вид
имеет
вид
![]()
где ![]() -
параметры (коэффициенты) регрессии,
-
регрессоры (факторы модели), k-
количество факторов модели.
-
параметры (коэффициенты) регрессии,
-
регрессоры (факторы модели), k-
количество факторов модели.
Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):
![]()
Параметр ![]() ,
при котором нет факторов, называют
часто константой.
Формально - это значение функции при
нулевом значении всех факторов. Для
аналитических целей удобно считать,
что константа - это параметр при "факторе",
равном 1 (или другой произвольной
постоянной, поэтому константой называют
также и этот "фактор"). В таком
случае, если перенумеровать факторы и
параметры исходной модели с учетом
этого (оставив обозначение общего
количества факторов - k), то линейную
функцию регрессии можно записать в
следующем виде, формально не содержащем
константу:
,
при котором нет факторов, называют
часто константой.
Формально - это значение функции при
нулевом значении всех факторов. Для
аналитических целей удобно считать,
что константа - это параметр при "факторе",
равном 1 (или другой произвольной
постоянной, поэтому константой называют
также и этот "фактор"). В таком
случае, если перенумеровать факторы и
параметры исходной модели с учетом
этого (оставив обозначение общего
количества факторов - k), то линейную
функцию регрессии можно записать в
следующем виде, формально не содержащем
константу:

![]() -
вектор регрессоров,
-
вектор регрессоров, ![]() -
вектор-столбец параметров (коэффициентов)
-
вектор-столбец параметров (коэффициентов)
Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно.
Пусть
дана выборка объемом
n наблюдений переменных y и x.
Обозначим t -
номер наблюдения в выборке. Тогда ![]() -
значение переменной y в t-м
наблюдении,
-
значение переменной y в t-м
наблюдении, ![]() -
значение j-го
фактора в t-м
наблюдении. Соответственно,
-
значение j-го
фактора в t-м
наблюдении. Соответственно, ![]() -
вектор регрессоров в t-м
наблюдении. Тогда линейная регрессионная
зависимость имеет место в каждом
наблюдении:
-
вектор регрессоров в t-м
наблюдении. Тогда линейная регрессионная
зависимость имеет место в каждом
наблюдении:
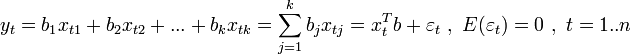
Введем обозначения:
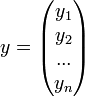 -
вектор наблюдений зависимой переменой y,
-
вектор наблюдений зависимой переменой y, 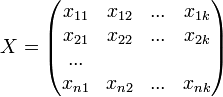 -
матрица факторов.
-
матрица факторов. 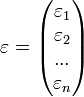 -
вектор случайных ошибок.
-
вектор случайных ошибок.
Тогда модель линейной регрессии можно представить в матричной форме:
![]()
Нелинейная регрессия — частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.
Задана выборка из ![]() пар
пар ![]() .
Задана регрессионная
модель
.
Задана регрессионная
модель ![]() ,
которая зависит от параметров
,
которая зависит от параметров ![]() и
свободной переменной
и
свободной переменной ![]() .
Требуется найти такие значения параметров,
которые доставляли бы минимум сумме
квадратов регрессионных
остатков
.
Требуется найти такие значения параметров,
которые доставляли бы минимум сумме
квадратов регрессионных
остатков
![]()
где
остатки ![]() для
для ![]() .
.
Для
нахождения минимума функции ![]() ,
приравняем к нулю её первые частные
производные параметрам
,
приравняем к нулю её первые частные
производные параметрам ![]() :
:
![]()
Так
как функция
в
общем случае не имеет единственного
минимума[1],
то предлагается назначить начальное
значение вектора параметров ![]() и приближаться
к оптимальному вектору по шагам:
и приближаться
к оптимальному вектору по шагам:
![]()
Здесь ![]() -
номер итерации,
-
номер итерации, ![]() -
вектор шага.
-
вектор шага.
На
каждом шаге итерации линеаризуем модель
с помощью приближения рядом
Тейлора относительно
параметров ![]()
Здесь
элемент матрицы Якоби ![]() -
функция параметра
-
функция параметра ![]() ;
значение свободной переменной
;
значение свободной переменной ![]() фиксировано.
В терминах линеаризованной модели
фиксировано.
В терминах линеаризованной модели
![]()
и регрессионные остатки определены как
![]()
Подставляя последнее выражение в выражение (*), получаем
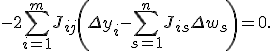
Преобразуя,
получаем систему из ![]() линейных
уравнений, которые называются нормальным
уравнением
линейных
уравнений, которые называются нормальным
уравнением
![]()
Запишем нормальное уравнение в матричном обозначении как
![]()
В том случае, когда критерий оптимальности регрессионой модели задан как взвешенная сумма квадратов остатков
![]()
нормальное уравнение будет иметь вид
![]()
Для нахождения оптимальных параметров нелинейных регрессионных моделей используются метод сопряжённых градиентов, метод Ньютона-Гаусса или алгоритм Левенберга-Марквардта.
Основная идея методов аппроксимации заключается в том, что исходная функция f(x) описывается в виде некоторого полинома fa(x), достаточно хорошо приближающего исходную функцию. Затем ищется точка минимума x* полинома fa(x), которая является оценкой истинной точки минимума. Ясно, что точность такой оценки определяется тем, насколько хорошо подобрана аппроксимирующая функция.
Согласно теореме Вейерштрасса об аппроксимации, если функция непрерывна в некотором интервале, то ее с любой степенью точности можно аппроксимировать полиномом достаточно высокого порядка. Качество оценок точки минимума аппроксимирующего полинома можно повысить двумя способами: использованием полинома более высокого порядка и уменьшением интервала аппроксимации.
Практика показывает, что второй способ, вообще говоря, является более предпочтительным, поскольку построение аппроксимирующего полинома порядка выше третьего становится весьма сложной процедурой, тогда как уменьшение интервала в условиях, когда выполняется предположение об унимодальности функции, особой сложности не представляет.
Квадратичная аппроксимация является простейшим вариантом полиномиальной интерполяции, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной.
Если задана последовательность точек x1, x2, x3 и известны соответствующие этим точкам значения функции f1, f2, f3, то можно определить постоянные величины a0, a1 и a2 таким образом, что значения квадратичной функции
q(x)=a0 + a1(x-x1)+a2(x-x1)(x-x2) (1.24)
совпадут со значениями f(x) в трех указанных точках. Перейдем к вычислению q(x) в каждой из трех заданных точек. Прежде всего, так как
f1=f(x1)=q(x1)=a0,
имеем a0=f1.
Далее, поскольку
f2=f(x2)=q(x2)=f1+ a1(x2-x1),
получаем
a1=(f2-f1)/(x2-x1).
Наконец, при x=x3
f3=f(x3)=q(x3)=f1+(f2-f1)/(x2-x1)(x3-x1)+a2(x3-x1)(x3-x2).
Разрешая последнее уравнение относительно a2, получаем
a2=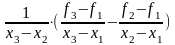 .
.
Таким образом показано, что по трем заданным точкам и соответствующим значениям функции можно оценить параметры a0, a1 и a2 аппроксимирующего квадратичного полинома с помощью приведенных выше формул.
Если точность аппроксимации исследуемой функции в интервале [x1, x3] c помощью указанного полинома оказывается достаточно высокой, то в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координат точки минимума.
В данном случае, согласно необходимому условию экстремума, найдя первую производную полинома и приравняв ее нулю, получим
q'(x)= a1+a2(x-x2)+a2(x-x1)=0,
откуда искомая оценка минимума равна
xa*=(x2-x1)/2 - (a1/2a2).
Алгоритм последовательной квадратичной аппроксимации
Задано: x1-начальная точка,
x-величина шага по оси x.
Вычислить x2=x1+x.
Вычислить f1=f(x1) и f2=f2(x2).
Если f1> f2, то x3=x1+2x;
иначе x3=x1-2x.
Вычислить f3=f(x3)
и найти
fmin=min{f1, f2, f3},
xmin-точка, которой соответствует fmin.
Вычислить xa* по трем точкам x1, x2 и x3 в соответствии с формулой квадратичной аппроксимации.
Вычислить [fmin-f(xa*)] и (xmin- xa*).
Если обе разности достаточно малы, то Стоп.
Выбрать "наилучшую" точку из xmin и xa* и две точки по обе стороны от нее. Пронумеровать эти точки в естественном порядке и перейти к 4.
Заметим, что при первой реализации шага 5 границы интервала, содержащего точку минимума, не обязательно оказываются установленными. При этом полученная точка xа* может находиться за точкой x3. Для того чтобы исключить возможность слишком большого экстраполяционного перемещения, следует провести после шага 5 дополнительную проверку и в случае, когда точка xа* находится слишком далеко от x3, заменить xа* точкой, координата которой вычисляется с учетом заранее установленной длины шага.
В соответствии с рассматриваемым методом минимизируемая функция f аппроксимируется полиномом третьего порядка. Логическая схема метода аналогична схеме методов с использованием квадратичной аппроксимации. Однако в данном случае построение аппроксимирующего полинома проводится на основе меньшего количества точек, поскольку в каждой точке можно вычислять как значение функции, так и ее производной.
Работа алгоритма начинается в точке x1, задаваемой пользователем, а затем находится другая точка x2, такая, что производные f'(x1) и f'(x2) имеют разные знаки. Это означает, что стационарная точка x*, в которой f'(x*)=0, будет лежать в интервале между выбранными точками x1 и x2.
Аппроксимирующая кубическая функция записывается в виде:
fa(x)=a0+a1(x-x1)+a2(x-x1)(x-x2)+ a3(x-x1)2(x-x2). (1.25)
Параметры уравнения (1.25) подбираются таким образом, чтобы значения fa(x) и ее производной в точках x1 и x2 совпадали со значениями f(x) и f’(x) в этих точках. Первая производная fa(x) равна
fa’(x)=a1+a2(x-x1)+a2(x-x2)(x-x2)+a3(x-x1)2+2a3(x-x1)(x-x2).(1.26)
Коэффициенты a0, a1, a2 и a3 уравнения (1.26) определяются по известным значениям f(x1), f(x2), f’(x1) и f’(x2) путем решения следующей системы линейных уравнений:
f1 = f(x1)=a0,
f2 =f(x2)=a0+a1(x2-x1),
f1’=f’(x1)=a1+a2(x1-x2),
f2’=f’(x2)=a1+a2(x2-x1)+a3(x2-x1)2.
Заметим, что данная система легко решается рекурсивным методом. После того как коэффициенты найдены, действуя по аналогии со случаем квадратичной аппроксимации, можно оценить координату стационарной точки функции f c помощью аппроксимирующего полинома (1.25). При этом приравнивание к нулю производной (1.26) приводит к квадратному уравнению. Используя формулу для вычисления корней квадратного уравнения, запишем решение, определяющее стационарную точку аппроксимирующего кубического полинома, в следующем виде:
xa*= ,
(1.27)
,
(1.27)
где
=(f2’+w-z)/(f2’-f1’+2w),
z =3(f1-f2)/(x2-x1)+f1’+f2’,
(z2-f1’f2’)1/2, если x1<x2,
w =
-(z2-f1’f2’)1/2, если x1<x2.
Формула для w обеспечивает надлежащий выбор одного из двух корней квадратного уравнения; для значений , заключенных в интервале от 0 до 1, формула (1.27) гарантирует, что получаемая точка xа* расположена между x1 и x2.
Затем снова выбираются две точки для реализации процедуры кубической аппроксимации - xа* и одна из точек x1 и x2, причем значения производной исследуемой функции в этих точках должны быть противоположны по знаку, и процедура кубичной аппроксимации повторяется.
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путёмдискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Дискретизация сигнала по времени. Спектр дискретного сигнала
Итак пара непрерывного преобразования Фурье (интеграл Фурье) имеет вид:
|
(1) |
где ![]() –
спектр сигнала
–
спектр сигнала ![]() (в
общем случае и сигнал и спектр —
комплексные).
(в
общем случае и сигнал и спектр —
комплексные).
Выражения для прямого ДПФ и обратного дискретного преобразования Фурье (ОДПФ) имеют вид:
|
(2) |
Выражение
для ДПФ ставит в соответствие ![]() отсчетам
сигнала
отсчетам
сигнала ![]() ,
, ![]() ,
в общем случае комплексного,
отсчетов
спектра
,
в общем случае комплексного,
отсчетов
спектра ![]() ,
, ![]() .
.
Можно
обратить внимание, что как и в непрерывном,
так и в дискретном случае, в выражении
для обратного преобразования имеется
нормировочный коэффициент. В случае
интеграла Фурье это ![]() ,
в случае ОДПФ –
,
в случае ОДПФ – ![]() .
Можно отметить, что в случае непрерывного
преобразования нормировочный
коэффициент
.
Можно отметить, что в случае непрерывного
преобразования нормировочный
коэффициент 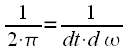 призван
корректно отображать масштабирование
сигнала во времени в частотную область
и наоборот. Другими словами, если
последовательно рассчитать спектр
некоторого сигнала, а после взять
обратное преобразование Фурье, то
результат обратного преобразования
должен полностью совпадать с исходным
сигналом. Нормировочный коэффициент
уменьшает
амплитуду сигнала на выходе обратного
преобразования для того чтобы она
совпадала с амплитудой исходного
сигнала.
призван
корректно отображать масштабирование
сигнала во времени в частотную область
и наоборот. Другими словами, если
последовательно рассчитать спектр
некоторого сигнала, а после взять
обратное преобразование Фурье, то
результат обратного преобразования
должен полностью совпадать с исходным
сигналом. Нормировочный коэффициент
уменьшает
амплитуду сигнала на выходе обратного
преобразования для того чтобы она
совпадала с амплитудой исходного
сигнала.
Рассмотрим
теперь сигнал ![]() ,
как результат умножения непрерывного
сигнала
на
решетчатую функцию
,
как результат умножения непрерывного
сигнала
на
решетчатую функцию
|
(3) |
где ![]() –
дельта-функция,
–
дельта-функция,
|
(4) |
![]() –
интервал
дискретизации. Графически процесс
дискретизации можно представить как
это показано на рисунке 1.
–
интервал
дискретизации. Графически процесс
дискретизации можно представить как
это показано на рисунке 1.
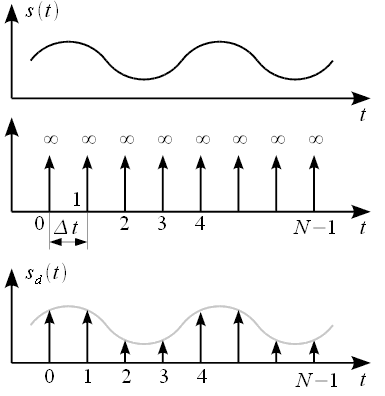 Рисунок
1: Процесс дискретизации сигнала
Рисунок
1: Процесс дискретизации сигнала
Вычислим спектр дискретного сигнала, для этого подставим выражения для дискретного сигнала (3) в выражения для преобразования Фурье (1), получим:
|
(5) |
Поменяем местами операции суммирования и интегрирования и вспомним фильтрующее свойство дельта-функции:
|
(6) |
Тогда выражение (5) с учетом (6):
|
(7) |
Таким
образом мы избавились от интегрирования
в бесконечных пределах, заменив конечным
суммированием комплексных экспонент.
Но пока частота ![]() меняется
на всей числовой оси. Однако можно
заметить что комплексные экспоненты
под знаком суммы в выражении (7) являются
периодическими функциями с периодом:
меняется
на всей числовой оси. Однако можно
заметить что комплексные экспоненты
под знаком суммы в выражении (7) являются
периодическими функциями с периодом:
|
(8) |
Необходимо
отметить, что ![]() исключено
из выражения (8), так как при
комплексная
экспонента равна единице для всех
частот. Таким образом максимальный
период повторения спектра
будет
при
исключено
из выражения (8), так как при
комплексная
экспонента равна единице для всех
частот. Таким образом максимальный
период повторения спектра
будет
при ![]() и
равен
и
равен
|
(9) |
В
результате можно рассматривать только
один период повторения спектра
при ![]()
Повторение сигнала во времени. Дискретное преобразование Фурье
Для
цифровой обработки требуются как
дискретные отсчеты сигнала, так и
дискретные отсчеты спектра. Известно
что дискретный (или как еще говорят
линейчатый спектр) имеют периодические
сигналы, а линейчатый спектр получается
путем разложения в ряд Фурье периодического
сигнала. Значит, чтобы получить дискретный
спектр, надо сделать исходный дискретный
сигнал периодическим, или другими
словами необходимо повторить данный
сигнал во времени бесконечное количество
раз с некоторым периодом ![]() ,
тогда его спектр будет содержать
дискретные гармоники кратные
,
тогда его спектр будет содержать
дискретные гармоники кратные ![]() .
Графически процесс повторения сигнала
во времени представлен на рисунке 2.
.
Графически процесс повторения сигнала
во времени представлен на рисунке 2.
 Рисунок
2: Повторение сигнала во времени
Рисунок
2: Повторение сигнала во времени
Черным показан исходный сигнал, серым его повторения через некоторый период .
Как
следует из рисунка 2, повторять сигнал
можно с различным периодом
,
однако необходимо чтобы период повторения
был более или равен длительности сигнала,
т.е. ![]() .
При этом минимальный период повторения
сигнала
.
При этом минимальный период повторения
сигнала
|
(10) |
Это
тот минимальный период при котором
сигнал и его повторения не накладываются
друг на друга. Повторение сигнала с
минимальным периодом ![]() представлен
на рисунке 3.
представлен
на рисунке 3.
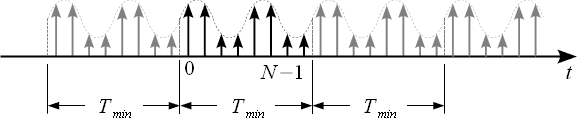 Рисунок
3: Повторение сигнала с минимальным
периодом
Рисунок
3: Повторение сигнала с минимальным
периодом
При повторении сигнала с минимальным периодом получим линейчатый спектр сигнала, состоящий из гармоник кратных
|
(11) |
и
на одном периоде ![]() получим
получим
|
(12) |
гармоник спектра.
Таким
образом мы можем продискретизировать
спектр дискретного сигнала на одном
периоде повторения
с
шагом  и
получим тем самым
отсчетов
спектра. Учтем вышесказанное в выражении
(7), получим:
и
получим тем самым
отсчетов
спектра. Учтем вышесказанное в выражении
(7), получим:
|
(13) |
Если
опустить в выражении (13) шаг дискретизации
по времени
и
по частоте ![]() ,
то получим окончательное выражение для
ДПФ:
,
то получим окончательное выражение для
ДПФ:
|
(14) |
Можно сделать вывод, что ДПФ ставит в соответствие отсчетам дискретного сигнала отсчетов дискретного спектра, при этом предполагается, что и сигнал и спектр являются периодическими и анализируются на одном периоде.
Численные методы дифференцирования и интегрирования (конечно-разностные аппроксимации производных; использование интерполяционного многочлена Лагранжа для численного дифференцирования; квадратурные формулы прямоугольников, трапеций и Симпсона для численного интегрирования).
Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
Основными задачами являются вычисление производной на краях таблицы и в ее середине. Для равномерной сетки формулы численного дифференцирования «в начале таблицы» можно представить в общем виде следующим образом:
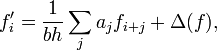
где ![]() —
погрешность формулы. Здесь
коэффициенты
—
погрешность формулы. Здесь
коэффициенты ![]() и
и ![]() зависят
от степени n использовавшегося
интерполяционного многочлена, то есть
от необходимой точности (скорости
сходимости к точному значению при
уменьшении шага сетки) формулы.
зависят
от степени n использовавшегося
интерполяционного многочлена, то есть
от необходимой точности (скорости
сходимости к точному значению при
уменьшении шага сетки) формулы.
При решении практических задач часто нужно найти производные указанных порядков от функции y=f(x). Возможно, что в силу сложности аналитического выражения функции f(x) непосредственное ее дифференцирование затруднено. В этих случаях обычно используют приближенные численные методы дифференцирования функций.
Идея всех методов численного дифференцирования сводится к замене исходной функции f(x) некоторой функцией P(x), ее интерполирующей (чаще всего полиномом или сплайном). Затем полагают:
 (9.1)
(9.1)
Если для интерполирующей функции известна погрешность R(x)=f(x)-P(x), то погрешность вычисления производной функции f(x) может быть вычислена по формуле
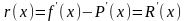 (9.2)
(9.2)
Следует отметить, что численное дифференцирование представляет собой операцию, менее точную, чем интегрирование. Близость друг к другу ординат двух кривых y=f(x)=P(x) на [a,b] еще не гарантирует близость на этом отрезке их производных, т.е. малого расхождения угловых коэффициентов касательных к графикам рассматриваемых кривых (рис. 9.1.).
Использование сплайнов со специально выбранными граничными условиями, уменьшающими осцилляцию сплайна между узлами интерполяции во многих случаях может существенно повысить точность вычисления производной функции.
Пусть имеем функцию y=f(x), заданную в равноотстоящих точках
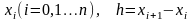
Введем
переменную
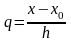 ,
тогда интерполяционная формула Ньютона
имеет вид
,
тогда интерполяционная формула Ньютона
имеет вид
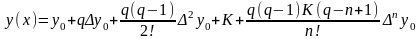
или
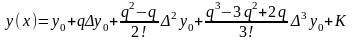 (9.3)
(9.3)
Учитывая, что
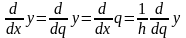
имеем
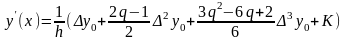 (9.4)
(9.4)
Для вычисления второй производной, дифференцируя (9. 4), получим:
 (9.5)
(9.5)
Аналогично можно получить формулу для вычисления производных более высоких порядков.
Если
производная функции вычисляется в точке

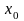 , то учитывая, что q=0,
имеем следующие формулы для вычисления
дифференциалов функции f(x):
, то учитывая, что q=0,
имеем следующие формулы для вычисления
дифференциалов функции f(x):
 (9.6)
(9.6)
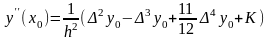 (9.7)
(9.7)
Оценка погрешности вычисления производных функций.
Ранее было показано, что . Для формулы Ньютона имеем:
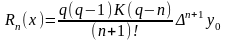
Тогда
 (9.8)
(9.8)
Конечно-разностные аппроксимации производных.
Основная идея метода заключается в замене частных производных их разностными аналогами. Рисунок 1.2 (графическая интерпретация некоторых конечно-разностных аппроксимаций для производных).
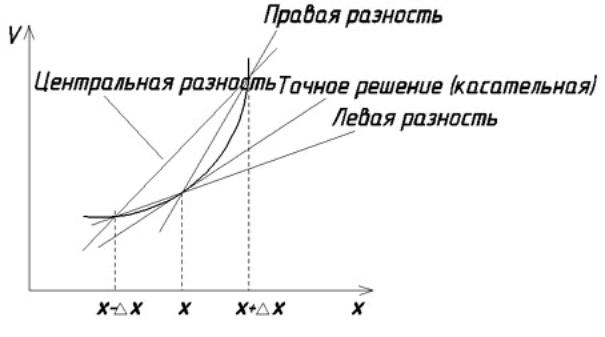
Рисунок 1.2.
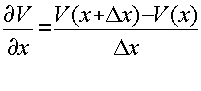 -
правая схема
-
правая схема
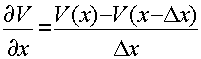 -
левая схема
-
левая схема
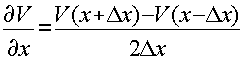 -
центральная схема
-
центральная схема
Получение разностных аналогов:
(1)
(2)
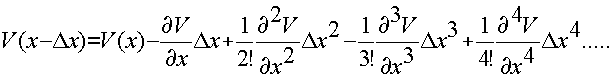
Центральная разность (1) - (2):
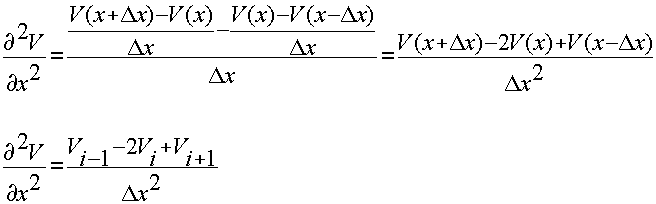
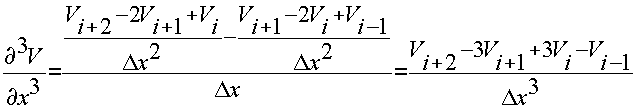
Алгоритм метода конечных разностей
Метод конечных разностей (МКР) является старейшим методом решения краевых задач.
Алгоритм (рис 1.3) МКР состоит из этапов традиционных для метода сеток:
1. Построение сетки в заданной области. В МКР используется сетка, задаваемая конечным множеством узлов. В узлах сетки определяются приближенные значения φh искомой функции φ. Совокупность узловых значений φhназывают сеточной функцией.
2. Замена дифференциального оператора Lh=∂φ/∂u в исходном дифференциальном уравнении разностным аналогом Lh, построенным по одной из схем, рассмотренных ниже. При этом непрерывная функция φ аппроксимируется сеточной функцией φh.
3. Если есть граничные условия второго и третьего рода, то для граничного узла с этим условием записывается соответствующая аппроксимация. В результате должна получиться замкнутая система НАУ.
4. Решение полученной системы алгебраических уравнений.
Использование интерполяционных многочленов Лагранжа для формул численного дифференцирования
Пусть
функция ![]() определена
на отрезке
определена
на отрезке ![]() и
в точках
и
в точках ![]()
![]() этого
отрезка принимает значение
этого
отрезка принимает значение ![]() .
.
Разность
между соседними значениями
аргумента ![]() постоянна
и является шагом
постоянна
и является шагом ![]() разбиением
отрезка на
частей,
причём
разбиением
отрезка на
частей,
причём ![]() и
и ![]() .
.
Найдём
аппроксимации производных первого и
второго порядков с помощью значений
функций ![]() в
узловых точках
с
погрешностью одного и того же порядка
в зависимости от шага
в
узловых точках
с
погрешностью одного и того же порядка
в зависимости от шага ![]()
Для
того чтобы выразить значения производных
через значения функции
в
узлах интерполяции ![]() построим
интерполяционный многочлен
Лагранжа
построим
интерполяционный многочлен
Лагранжа ![]() степени
степени ![]() ,
удовлетворяющий условиям
,
удовлетворяющий условиям
![]()
![]()
![]()
Многочлен
интерполирует
функцию ![]() на
отрезке
на
отрезке ![]() Дифференцируя
многочлен
,
получаем значения производных в
точках
Дифференцируя
многочлен
,
получаем значения производных в
точках ![]()
![]()
Если ![]() ,
то
,
то ![]() –
линейная функция, график которой проходит
через точки
–
линейная функция, график которой проходит
через точки ![]() и
и ![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
.
Если ![]() ,
то график интерполяционного многочлена
Лагранжа
,
то график интерполяционного многочлена
Лагранжа ![]() − парабола,
проходящая через три точки
,
и
− парабола,
проходящая через три точки
,
и ![]() .
Вычислим первую и вторую производные
многочлена
на
отрезке
.
Вычислим первую и вторую производные
многочлена
на
отрезке ![]() :
:
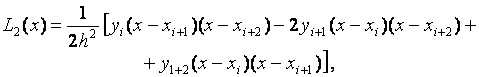
![]()
![]()
Первая
и вторая производные многочлена
Лагранжа
в
точках ![]() являются
приближениями соответствующих производных
функции
в
этих точках:
являются
приближениями соответствующих производных
функции
в
этих точках:
 (6.4)
(6.4)
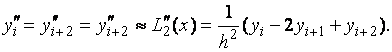 (6.5)
(6.5)
Если функция на отрезке имеет непрерывную производную до третьего порядка включительно, то справедливо представление функции в виде суммы:
![]() (6.6)
(6.6)
где ![]() −
остаточный член интерполяционной
формулы, причём
−
остаточный член интерполяционной
формулы, причём
![]() ,
, ![]() .
.
В этом случае можно дать оценку погрешности приближений производных соотношениями (6.4) и (6.5). Дифференцируя (6.6), получим
![]() (6.7)
(6.7)
![]() (6.8)
(6.8)
![]()
![]() (6.9)
(6.9)
![]() .
(6.10)
.
(6.10)
Погрешности при вычислении производных в точках определяются из формул (6.7)–(6.9) следующими значениями остатков:
![]() (6.11)
(6.11)
![]()
![]()
![]() (6.12)
(6.12)
Таким
образом, равенства (6.11) показывают, что
погрешности аппроксимации первой
производной ![]() с
помощью формул (6.4) имеют один и тот же
порядок
с
помощью формул (6.4) имеют один и тот же
порядок ![]() ,
и естественна следующая рекомендация
по их применению на отрезке
,
и естественна следующая рекомендация
по их применению на отрезке ![]() в
точках
в
точках ![]() при
при ![]() :
:
![]()
![]()
![]() (6.13)
(6.13)
![]() .
.
Из
равенств (6.13) следует, что приближение
второй производной с помощью формулы
(6.5) имеет различный порядок в
зависимости от ![]() в разных
точках: в точках
в разных
точках: в точках ![]() имеется
погрешность порядка
,
а в точке
имеется
погрешность порядка
,
а в точке![]() порядок
погрешности выше
порядок
погрешности выше ![]() .
.
В
случае интерполяции функции
,
имеющей на отрезке
непрерывную
производную до четвёртого порядка
включительно, можно получить погрешность
интерполяции второй производной, имеющую
порядок ![]() и
одинаковую во всех точках, с помощью
многочлена Лагранжа третьей степени
и
одинаковую во всех точках, с помощью
многочлена Лагранжа третьей степени ![]() по
четырём узлам интерполяции
по
четырём узлам интерполяции ![]()
![]() .
Опуская выкладки, приведём результаты
для аппроксимации второй производной:
.
Опуская выкладки, приведём результаты
для аппроксимации второй производной:
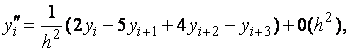
 (6.14)
(6.14)
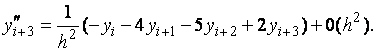
Формулы
(6.14) дают порядок аппроксимации ![]() для
производных первого порядка функции
,
непрерывно-дифференцируемой до третьего
порядка включительно на отрезке
.
Этот порядок сохраняется при вычислении
производной второго порядка на отрезке
в
точках
при
для
производных первого порядка функции
,
непрерывно-дифференцируемой до третьего
порядка включительно на отрезке
.
Этот порядок сохраняется при вычислении
производной второго порядка на отрезке
в
точках
при ![]() по
формулам:
по
формулам:

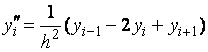 (6.15)
(6.15)
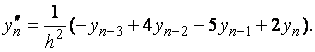
Если
функция
на
отрезке ![]() имеет
непрерывную производную до
имеет
непрерывную производную до ![]() -го
порядка включительно, то справедливо
представление
-го
порядка включительно, то справедливо
представление ![]() ,
где
−
интерполяционный многочлен Лагранжа
степени
,
аппроксимирующий функцию
по
узлам интерполяции
,
где
−
интерполяционный многочлен Лагранжа
степени
,
аппроксимирующий функцию
по
узлам интерполяции ![]()
![]()
![]() −
остаточный член интерполяционной
формулы, причём
−
остаточный член интерполяционной
формулы, причём
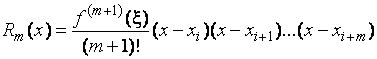 ,
, ![]() .
.
Далее, используя приведённую схему и выбирая подходящую степень интерполяционного многочлена, можно добиться нужной точности при аппроксимации производных различных порядков.
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Численное интегрирование применяется, когда:
Сама подинтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.
Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например,
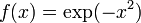 .
.
При решении задач научного и инженерно-технического характера математическими методами часто возникает необходимость проинтегрировать какую-либо функцию. Есть функции, которые невозможно интегрировать аналитически, т.е. только в некоторых случаях по заданной функции можно найти первообразную. Общим способом интегрирования любых функций является численное интегрирование, методы которого в большинстве своем просты и легко переводятся на алгоритмические языки.
Геометрически интеграл функции f(x) в пределах от a до b представляет собой площадь криволинейной трапеции, ограниченной графиком этой функции, осью x и прямыми x = a и x = b.
Численные методы интегрирования используют замену площади криволинейной трапеции на конечную сумму площадей более простых геометрических фигур, которые могут быть вычислены точно. В этом смысле говорят об использовании квадратурных формул (по аналогии с задачей о квадратуре круга – построение квадрата с площадью, равной площади круга с определенным радиусом).
В большинстве методов используется приближенной представление интеграла в виде конечной суммы (квадратурная формула):
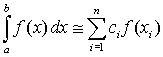
где ci – постоянные, называемые весами, а xi – принадлежат интервалу [ a, b] и называютсяузлами.
В основе квадратурных формул лежит идея аппроксимации на отрезке интегрирования графика подынтегрального выражения функциями более простого вида, которые легко могут быть проинтегрированы аналитически и, таким образом, легко вычислены. Наиболее просто задача построения квадратурных формул реализуется для полиномиальных математических моделей.
Многочлен (полином) порядка n имеет вид
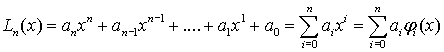 ,
,
и
определяется, таким образом, значениями
(n+1) констант ai .
Если известно значение функции в (n+1)
точках ![]() i =
0, 1, …, n,
то данные параметры легко определяются
из системы (n+1)
линейных уравнений с (n+1) переменными ai
i =
0, 1, …, n,
то данные параметры легко определяются
из системы (n+1)
линейных уравнений с (n+1) переменными ai
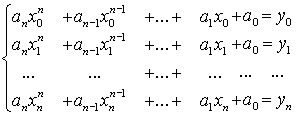
Если все xi различны, то данная система уравнений имеет единственное решение, так как определитель системы, составленный из коэффициентов системы линейных уравнений (так называемый определитель Вандермонда) будет отличен от нуля
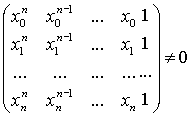
Определив коэффициенты интерполяционного многочлена, можно легко вычислить приближенное значение интеграла, заменив подынтегральную функцию на полученный многочлен

Узлы интерполирования на отрезке интегрирования могут быть расположены на равном удалении друг от друга (эквидистантные узлы). В этом случае для полинома степени n имеем следующее
![]() ,
, ![]() ,
, ![]()
![]()
h – шаг, xi – узлы интерполирования.
При n = 0 получаем метод прямоугольников. График функции f(x) на отрезке интегрирования заменяется на горизонтальную линию (полином степени 0).
Ф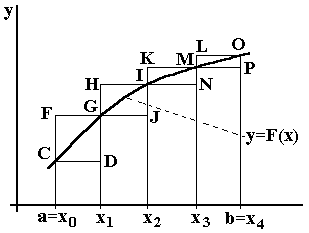 ормула
прямоугольников.
ормула
прямоугольников.
Интегрирование методом прямоугольников (метод Эйлера).
Пусть функцию (рисунок справа ) необходимо проинтегрировать численным методом на отрезке [a, b]. Разделим отрезок на N равных интервалов (на рисунке N = 4).
Площадь каждой из 4-х криволинейных трапеций можно заменить на площадь прямоугольника.
Ширина
всех прямоугольников одинакова и равна ![]()
В качестве выбора высоты прямоугольников можно предложить выбрать значение функции на левой границе. В этом случае высота первого прямоугольника составит f(a), второго – f(x1), третьего – f(x2), последнего – f(x3). Приближенное значение интеграла получается суммированием площадей прямоугольников
![]()
Если в качестве выбора высоты прямоугольников взять значение функции на правой границе, то в этом случае высота первого прямоугольника составит f(x1), второго – f(x2), третьего – f(x3), последнего – f(b).
![]()
Как видно, в этом случае, одна из формул дает приближение к интегралу с избытком, а вторая c недостатком. Можно предложить еще один способ, очевидно лучший, чем обе эти формулы – использовать для аппроксимации значение функции в середине отрезка интегрирования.
![]()
В общем виде, если отрезок [a, b] разбить на N равных интервалов интегрирования (h) и к каждому интервалу применить формулу прямоугольников, то получим
![]()

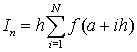


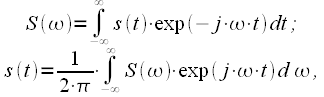
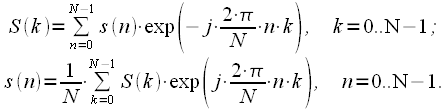
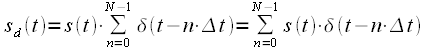 ,
,
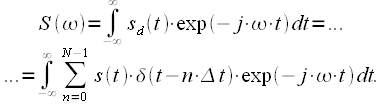
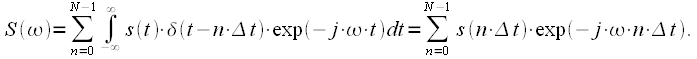

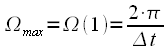 .
.