
- •Основы информационных технологий (теория систем, дискретная и компьютерная математика, теория управления, моделирование) (Первые вопросы в билетах).
- •Интерполирование функций (многочленами Лагранжа; интерполяционная формула Ньютона; интерполяция кубическими сплайнами).
- •Приближение функций (метод наименьших квадратов; линейная регрессия; нелинейная регрессия; полиномиальная аппроксимация; дискретное преобразование Фурье).
- •Формула трапеций
- •Численное решение систем линейных алгебраических уравнений (метод Гаусса; метод итераций).
- •11. Универсальный метод информационных технологий – статистическое моделирование нелинейных систем со случайными характеристиками в условиях помех (метод Монте-Карло).
- •!!!13 И 14 вопросы отсутствуют в билетах!!!
- •!!!16 Вопрос отсутствует в билетах!!!
- •1.2.1. Принцип разомкнутого управления
- •1.2.2. Принцип компенсации
- •1.2.3. Принцип обратной связи
- •1. Введение
- •2. Итерационные методы Якоби и Зейделя
- •3. Метод последовательной верхней релаксации
- •4. Матрично-векторное представление итерационных методов
- •Динамические модели в экономике (регрессионные, авторегрессионные, регрессионно-авторегрессионные модели; модели накопления и дисконтирования; модели «затраты-выпуск»).
- •Основы вычислительной техники. (Вторые вопросы в билетах)
- •Характеристики современных операционных систем (многопоточность, симметричная многопроцессорность, распределенные операционные системы, объектно-ориентированный дизайн).
- •Дискретный сигнал
- •Вычислительные сети и системы (протоколы обмена тср, iр, ssl, skip, NetBeui, ipx, spx, NetBios, модель osi, типы соединения эвм, используемые при построении локальных сетей).
- •Информация (аналоговая и цифровая информация, оценки количества информации, энтропийный подход).
- •Структура микропроцессора (алу, регистры: аккумуляторы, ввода-вывода, понятие шины: шина данных, адресная шина, шина команд; запоминающие устройства: пзу, озу, созу, кэш-память).
- •!!!16 Вопроса нет в билетах!!!
- •17. Понятие нелинейных преобразователей (транзисторы, ключи, диодные выпрямители, логические элементы, нейронные сети).
- •1.8. Основные методы расчета сложных электрических цепей
- •19. Расчет комплексных сопротивлений линейных цепей (последовательные цепи: rc-цепь, rl-цепь, rlc-цепь; параллельные цепи: rc-цепь, rl-цепь, lc-цепь; последовательно-параллельные цепи: r-lc, c-rl).
- •Основы алгоритмизации и программирования. (Третьи вопросы в билетах)
- •2. Методы сортировки и поиска данных в массивах и файлах. Оценки скорости.
- •Современные языки программирования (с, Java, Delphi, vb). Типы данных языка. Структура приложения.
- •Примитивные типы
- •Типы данных
- •Объекты
- •Статическая и динамическая память, определение, область применения. Алгоритмы обработки очереди, списка, стека.
- •4 Шага добавления
- •Основные компоненты в языках (с, Java, Delphi). Их свойства, методы, события. Реализация графики.
- •7. Понятия объектно-ориентированного программирования. Поля, свойства, методы, события. Область видимости. Пример класса.
- •Базы данных. Типы бд. Реляционные бд. Типы полей. Типы связей. Язык запросов sql. Индексирование баз данных.
- •Создание Internet-приложений (на стороне клиента и сервера). Язык разметки гипертекста html. Специализированные инструменты (php). Создание Internet-приложений средствами языков с, Java, Delphi.
- •Глава 1 – содержание элемента html
- •6.3. Рисунки
- •Основные элементы блок схем программирования, типовые блок схемы (ввода-вывода, исполнения команд, условного перехода; ветвящиеся программы, циклические программы, вложенные циклы).
!!!16 Вопроса нет в билетах!!!
17. Понятие нелинейных преобразователей (транзисторы, ключи, диодные выпрямители, логические элементы, нейронные сети).
Нелинейность вольт-амперной характеристики полупроводниковых диодов может быть использована не только в схемах логарифмирования, но и во множестве других узлов, выполняющих различные нелинейные преобразования сигнала. Такие схемы носят название нелинейных преобразователей. Наиболее известны такие виды нелинейных преобразователей как: квадраторы, экстрематоры, усилители с возрастающим или убывающим коэффициентом передачи и т.п.
Транзи́стор (англ. transistor), полупроводниковый триод — радиоэлектронный компонент из полупроводникового материала, обычно с тремя выводами, позволяющий входным сигналам управлять током в электрической цепи. Обычно используется для усиления, генерации и преобразования электрических сигналов. В общем случае транзистором называют любое устройство, которое имитирует главное свойство транзистора - изменения сигнала между двумя различными состояниями при изменении сигнала на управляющем электроде.
В полевых и биполярных транзисторах управление током в выходной цепи осуществляется за счёт изменения входного напряжения или тока. Небольшое изменение входных величин может приводить к существенно большему изменению выходного напряжения и тока. Это усилительное свойство транзисторов используется в аналоговой технике (аналоговые ТВ, радио, связь и т. п.). В настоящее время в аналоговой технике доминируют биполярные транзисторы (БТ) (международный термин — BJT, bipolar junction transistor). Другой важнейшей отраслью электроники является цифровая техника (логика, память, процессоры, компьютеры, цифровая связь и т. п.), где, напротив, биполярные транзисторы почти полностью вытеснены полевыми.
В 1956 г. за изобретение транзистора Уильям Шокли, Джон Бардин и Уолтер Браттейн получили Нобелевскую премию по физике.
На принципиальных схемах обозначается «VT» или «Q». В русскоязычной литературе и документации до 1970-х гг. применялись обозначения «Т», «ПП» (полупроводниковый прибор) или «ПТ» (полупроводниковый триод).
Ниже приведена формальная классификация токовых транзисторов, где рабочее тело представляет собой поток носителей тока, а состояния между которыми переключается прибор определяется по величине сигнала: малый сигнал - большой сигнал, закрытое состояние - открытое состояние, на которых реализуется двоичная логика работы транзистора. Современная технология может оперировать не только электрическим зарядом, но и магнитными моментами, спином отдельного электрона, фононами и световыми квантами, квантовыми состояниями в общем случае.
По основному полупроводниковому материалу
Помимо основного полупроводникового материала, применяемого обычно в виде монокристалла, транзистор содержит в своей конструкции легирующие добавки к основному материалу, металлические выводы, изолирующие элементы, части корпуса (пластиковые или керамические). Иногда употребляются комбинированные наименования, частично описывающие материалы конкретной разновидности (например, «кремний на сапфире» или «металл-окисел-полупроводник»). Однако основными являются транзисторы на основе кремния, германия, арсенида галлия.
Другие материалы для транзисторов до недавнего времени не использовались. В настоящее время имеются транзисторы на основе, например, прозрачных полупроводников для использования в матрицах дисплеев. Перспективный материал для транзисторов — полупроводниковые полимеры. Также имеются отдельные сообщения о транзисторах на основе углеродных нанотрубок[3], о графеновых полевых транзисторах.
По структуре
|
|
|
Транзисторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Биполярные |
|
|
|
|
|
Полевые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
p-n-p |
|
n-p-n |
|
С p-n-переходом |
|
|
С изолированным затвором |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
С каналом n-типа |
|
С каналом p-типа |
|
Со встроенным каналом |
|
С индуцированным каналом |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Принцип действия и способы применения транзисторов существенно зависят от их типа и внутренней структуры, поэтому подробная информация об этом отнесена в соответствующие статьи.
Биполярные
n-p-n структуры, «обратной проводимости».
p-n-p структуры, «прямой проводимости»
В биполярном транзисторе носители заряда движутся от эмиттера через тонкую базу к коллектору. База отделена от эмиттера и коллектора pn переходами. Ток протекает через транзистор лишь тогда, когда носители заряда инжектируются из эмиттера в базу через pn переход. В базе они являются неосновными носителями заряда и легко проникают через другой pn переход между базой и коллектором, ускоряясь при этом. В самой базе носители заряда движутся за счет диффузионного механизма, поэтому база должна быть достаточно тонкой. Управления током между эмиттером и коллектором осуществляется изменением напряжения между базой и эмиттером, от которой зависят условия инжекции носителей заряда в базу.
Полевые
с p-n переходом
с изолированным затвором
В полевом транзисторе ток протекает от истока до стока через канал под затвором. Канал существует в легированном полупроводнике в промежутке между затвором и нелегированной подложкой, в которой нет носителей заряда, и она не может проводить ток. Преимущественно под затвором существует область обеднения, в которой тоже нет носителей заряда благодаря образованию между легированным полупроводником и металлическим затвором контакта Шоттки. Таким образом ширина канала ограничена пространством между подложкой и областью обеднения. Приложенное к затвору напряжение увеличивает или уменьшает ширину области обеднения и, тем самым, ширину канала, контролируя ток.
Однопереходные
Криогенные транзисторы (на эффекте Джозефсона)[источник не указан 1336 дней]
Многоэмиттерные транзисторы
Баллистические транзисторы
Одномолекулярный транзистор[4]
Комбинированные транзисторы
Транзисторы со встроенными резисторами (Resistor-equipped transistors (RETs)) — биполярные транзисторы со встроенными в один корпус резисторами.
Транзистор Дарлингтона — комбинация двух биполярных транзисторов, работающая как биполярный транзистор с высоким коэффициентом усиления по току.
на транзисторах одной структуры
на транзисторах разной структуры
Лямбда-диод — двухполюсник, комбинация из двух полевых транзисторов, имеющая, как и туннельный диод, значительный участок с отрицательным сопротивлением.
Биполярный транзистор, управляемый полевым транзистором с изолированным затвором (IGBT) — силовой электронный прибор, предназначенный в основном, для управления электрическими приводами
По мощности
По рассеиваемой в виде тепла мощности различают:
маломощные транзисторы до 100 мВт
транзисторы средней мощности от 0,1 до 1 Вт
мощные транзисторы (больше 1 Вт).
По исполнению
дискретные транзисторы
корпусные
Для свободного монтажа
Для установки на радиатор
Для автоматизированных систем пайки
бескорпусные
транзисторы в составе интегральных схем.
По материалу и конструкции корпуса
металло-стеклянный
пластмассовый
керамический
Прочие типы
Одноэлектронные транзисторы содержат квантовую точку (т. н. «остров») между двумя туннельными переходами. Ток туннелирования управляется напряжением на затворе, связанном с ним ёмкостной связью.[5]
Биотранзистор
Вне зависимости от типа транзистора, принцип применения его един:
Источник питания питает электрической энергией нагрузку, которой может быть громкоговоритель, реле, лампа накаливания, вход другого, более мощного транзистора, электронной лампы и т. п. Именно источник питания даёт нужную мощность для «раскачки» нагрузки.
Транзистор же используется для ограничения силы тока, поступающего в нагрузку, и включается в разрыв между источником питания и нагрузкой. То есть транзистор представляет собой некий вариант полупроводникового резистора, сопротивление которого можно очень быстро изменять.
Выходное сопротивление транзистора меняется в зависимости от напряжения на управляющем электроде. Важно то, что это напряжение, а также сила тока, потребляемая входной цепью транзистора, гораздо меньше напряжения и силы тока в выходной цепи. Таким образом, за счёт контролируемого управления источником питания достигается усиление сигнала.
Если мощности входного сигнала недостаточно для «раскачки» входной цепи применяемого транзистора, или конкретный транзистор не даёт нужного усиления, применяют каскадное включение транзисторов, когда более чувствительный и менее мощный транзистор управляет энергией источника питания на входе более мощного транзистора. Также подключение выхода одного транзистора ко входу другого может использоваться в генераторных схемах типа мультивибратора. В этом случае применяются одинаковые по мощности транзисторы.
Транзистор применяется в:
Усилительных схемах. Работает, как правило, в усилительном режиме.[6][7] Существуют экспериментальные разработки полностью цифровых усилителей, на основе ЦАП, состоящих из мощных транзисторов.[8][9] Транзисторы в таких усилителях работают в ключевом режиме.
Генераторах сигналов. В зависимости от типа генератора транзистор может использоваться либо в ключевом (генерация прямоугольных сигналов), либо в усилительном режиме (генерация сигналов произвольной формы).
Электронных ключах. Транзисторы работают в ключевом режиме. Ключевые схемы можно условно назвать усилителями (регенераторами) цифровых сигналов. Иногда электронные ключи применяют и для управления силой тока в аналоговой нагрузке. Это делается, когда нагрузка обладает достаточно большой инерционностью, а напряжение и сила тока в ней регулируются не амплитудой, а шириной импульсов. На подобном принципе основаны бытовые диммеры для ламп накаливания и нагревательных приборов, а такжеимпульсные источники питания.
Транзисторы применяются в качестве активных (усилительных) элементов в усилительных и переключательных каскадах. Реле и тиристоры имеют больший коэффициент усиления мощности, чем транзисторы, но работают только в ключевом (переключательном) режиме.
Вся современная цифровая техника построена, в основном, на полевых МОП (металл-оксид-полупроводник)-транзисторах (МОПТ), как более экономичных, по сравнению с БТ, элементах. Иногда их называют МДП (металл-диэлектрик-полупроводник)- транзисторы. Международный термин — MOSFET (metal-oxide-semiconductor field effect transistor). Транзисторы изготавливаются в рамках интегральной технологии на одном кремниевом кристалле (чипе) и составляют элементарный «кирпичик» для построения микросхем логики, памяти, процессора и т. п. Размеры современных МОПТ составляют от 90 до 22 нм[источник не указан 957 дней]. В настоящее время на одном современном кристалле площадью 1—2 см² могут разместиться несколько (пока единицы) миллиардов МОПТ. На протяжении 60 лет происходит уменьшение размеров (миниатюризация) МОПТ и увеличение их количества на одном чипе (степень интеграции), в ближайшие годы ожидается дальнейшее увеличение степени интеграции транзисторов на чипе (см. Закон Мура). Уменьшение размеров МОПТ приводит также к повышению быстродействия процессоров, снижению энергопотребления и тепловыделения.
В настоящее время микропроцессоры Intel собираются на трёхмерных транзисторах (3d транзисторы) именуемых Tri-Gate. Эта революционная технология позволила существенно улучшить существующие характеристики процессоров. Отметим, что переход к 3D-транзисторам при технологическом процессе 22 нм позволил повысить производительность процессоров на 30 % (по оценкам Intel) и снизить энергопотребление . Примечательно, что затраты на производство возрастут всего на 2—3 %, то есть в магазинах новые процессоры не будут значительно дороже старых[ . Суть технологии в том, что теперь сквозь затвор транзистора проходит особый High-K диэлектрик, который снижает токи утечки.
Ключ (переключатель, выключатель) — электрический коммутационный аппарат, служащий для замыкания и размыкания электрической цепи.
Ключи бывают механическими, электромагнитными и электронными.
Механические
Механические ключи служат для непосредственного управления цепью, так как диэлектрический рычаг механического ключа обычно напрямую связан с токоведущими частями ключа. Применяются обычно в случае, когда не требуется отделять управляемую цепь.
Выключатели освещения
Пакетные выключатели
Тумблеры
Переключатели различных конструкций: галетные, клавишные, движковые и др.
Электромагнитные
Электромагнитные ключи служат для дистанционного управления, управления высоковольтными цепями (в случаях, когда опасно управлять напрямую механическим ключом), гальванической развязки между устройством управления и нагрузками, синхронного управления несколькими цепями от одного сигнала.
Для защиты управляющей цепи от импульса самоиндукции, возникающей при снятии напряжения с обмотки, параллельно ей включают диод в направлении, обратном полярности управляющего напряжения. Данный способ неприменим при использовании обмотки, питаемой переменным током.
Реле
Шаговые искатели
Контакторы, магнитные пускатели
Электронные
Электронные ключи основаны на работе биполярных транзисторов. Когда на базе транзистора «0» относительно эмиттера, транзистор «закрыт», ток через него не идёт, на коллекторе всё напряжение питания (сигнал высокого уровня — «1»). Когда на базе транзистора «1», он «открыт», возникает ток коллектор-эмиттер и падение напряжения на сопротивлении коллектора, напряжение на коллекторе, а с ним и напряжение на выходе, уменьшается до низкого уровня «0».
Также возможно использование полевых транзисторов. Принцип их работы схож с принцип работы электронных ключей на биполярных транзисторах. Цифровые ключи на полевых транзисторах потребляют меньший ток управления, обеспечивают гальваническую развязку входных и выходных цепей, однако быстродействие их ниже по сравнению с биполярными.
Неуправляемые
Диод
Управляемые
Электронная лампа
Тиристор
Симистор
Транзистор
Транзисторный ключ — токовый ключ, выполненный на одном или нескольких транзисторах, работающих в ключевом режиме. Изменение электропроводности транзистора, обусловливающее переключение тока в нагрузке, обеспечивается подачей на его базу управляющего напряжения (сигнала) определённой полярности и уровня. Нагрузка, подключённая к транзисторному ключу, оказывается зашунтированной большим или малым сопротивлением транзистора. В ключевом режиме могут работать как обычные (полевые и биполярные) транзисторы, так и транзисторы, специально разработанные для работы в ключевом режиме (IGBT-транзисторы).
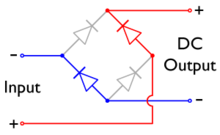
Дио́дный мо́ст — электрическая схема, предназначенная для преобразования («выпрямления») переменного тока в пульсирующий. Такое выпрямление называется двухполупериодным
Выполняется по мостовой схеме Гретца. Изначально она была разработана с применением радиоламп, но считалась сложным и дорогим решением, вместо неё применялась схема Миткевича со сдвоенной вторичной обмоткой в питающем выпрямитель трансформаторе. Сейчас, когда полупроводники очень дёшевы, в большинстве случаев применяется мостовая схема.
Вместо диодов в схеме могут применяться вентили любых типов — например селеновые столбы, принцип работы схемы от этого не изменится.
На вход (Input) схемы подаётся переменное напряжение (обычно, но не обязательно синусоидальное). В каждый из полупериодов ток проходит только через 2 диода, 2 других — заперты:
Выпрямление положительной полуволны |
|
Выпрямление отрицательной полуволны |
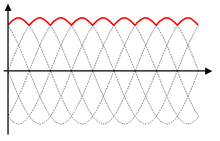
При выпрямлении 3-фазного тока 3-фазным выпрямителем результат получается ещё более «гладким»
В результате, на выходе (DC Output) получается напряжение, пульсирующее с частотой, вдвое большей частоты питающего напряжения:
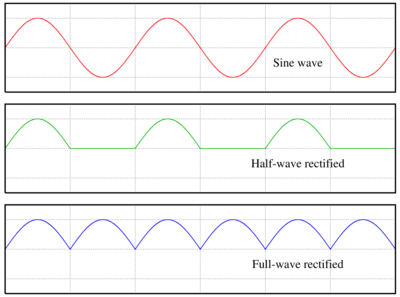
Красным — исходное синусоидальное напряжение , зелёным — однополупериодное выпрямление (для сравнения), синим — рассматриваемое двухполупериодное
Практически, для получения постоянного (а не пульсирующего) напряжения, схему надо дополнить фильтром на конденсаторе, а также, возможно, дросселем и стабилизатором напряжения.
Двухполупериодное выпрямление с помощью моста (по сравнению с однополупериодным) позволяет:
получить на выходе напряжение с повышенной частотой пульсаций, которое проще сгладить фильтром на конденсаторе
избежать постоянного тока подмагничивания в питающем мост трансформаторе
увеличить его КПД, что позволяет сделать его магнитопровод меньшего сечения.
Недостатки
Происходит двойное падение напряжения по сравнению с однополупериодным выпрямлением (прямое напряжение диода × 2 ≈ 1 В), это иногда нежелательно.
При перегорании одного из диодов схема превращается в однополупериодную, что может быть не замечено вовремя, и в устройстве появится скрытый дефект.
Мосты могут быть изготовлены из отдельных диодов, и могут быть выполнены в виде монолитной конструкции (диодная сборка).
Монолитная конструкция, как правило, предпочтительнее — она дешевле и меньше по объёму (хотя не всегда той формы, которая требуется). Диоды в ней подобраны на заводе и наверняка имеют одинаковые параметры и при работе находятся в одинаковом тепловом режиме. Сборку проще монтировать.
В монолитной конструкции при выходе из строя одного диода приходится менять весь монолит. В конструкции из отдельных диодов может меняться только один диод. Какую конструкцию применить решает конструктор, в зависимости от назначения устройства.
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
механические,
гидравлические,
пневматические,
электромагнитные,
электромеханические,
электронные.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
РТЛ (резисторно-транзисторная логика)
ДТЛ (диодно-транзисторная логика)
ТТЛ (транзисторно-транзисторная логика)
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
ТТЛШ (то же с диодами Шоттки)
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
КМОП (логика на основе комплементарных ключей на МОП транзисторах)
ЭСЛ (эмиттерно-связанная логика)
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Сумматор
Полусумматор
Делитель
Шифратор
Дешифратор
Мультиплексор
Демультиплексор
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
Триггер
Счётчик импульсов
Регистр
Венъюнктор
Секвентор
Иску́сственные нейро́нные се́ти (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса[1]. После разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.
С точки зрения машинного обучения, нейронная сеть представляет собой частный случай методов распознавания образов, дискриминантного анализа, методов кластеризации и т. п. С математической точки зрения, обучение нейронных сетей — это многопараметрическая задача нелинейной оптимизации. С точки зрения кибернетики, нейронная сеть используется в задачах адаптивного управления и как алгоритмы для робототехники. С точки зрения развития вычислительной техники и программирования, нейронная сеть — способ решения проблемы эффективного параллелизма[2]. А с точки зрения искусственного интеллекта, ИНС является основой философского течения коннективизма и основным направлением в структурном подходе по изучению возможности построения (моделирования) естественного интеллекта с помощью компьютерных алгоритмов.
Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что в случае успешного обучения сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке, а также неполных и/или «зашумленных», частично искаженных данных.
Известные применения.
Распознавание образов и классификация
В качестве образов могут выступать различные по своей природе объекты: символы текста, изображения, образцы звуков и т. д. При обучении сети предлагаются различные образцы образов с указанием того, к какому классу они относятся. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно[11]. По окончании обучения сети ей можно предъявлять неизвестные ранее образы и получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из её выходов должен появиться признак того, что образ принадлежит этому классу. В то же время на других выходах должен быть признак того, что образ данному классу не принадлежит[12]. Если на двух или более выходах есть признак принадлежности к классу, считается, что сеть «не уверена» в своём ответе.
Принятие решений и управление
Эта задача близка к задаче классификации. Классификации подлежат ситуации, характеристики которых поступают на вход нейронной сети. На выходе сети при этом должен появиться признак решения, которое она приняла. При этом в качестве входных сигналов используются различные критерии описания состояния управляемой системы[13].
Кластеризация
Под кластеризацией понимается разбиение множества входных сигналов на классы, при том, что ни количество, ни признаки классов заранее не известны. После обучения такая сеть способна определять, к какому классу относится входной сигнал. Сеть также может сигнализировать о том, что входной сигнал не относится ни к одному из выделенных классов — это является признаком новых, отсутствующих в обучающей выборке, данных. Таким образом, подобная сеть может выявлять новые, неизвестные ранее классы сигналов. Соответствие между классами, выделенными сетью, и классами, существующими в предметной области, устанавливается человеком. Кластеризацию осуществляют, например, нейронные сети Кохонена.
Нейронные сети в простом варианте Кохонена не могут быть огромными, поэтому их делят на гиперслои (гиперколонки) и ядра (микроколонки). Если сравнивать с мозгом человека, то идеальное количество параллельных слоёв не должно быть более 112. Эти слои в свою очередь составляют гиперслои (гиперколонку), в которой от 500 до 2000 микроколонок (ядер). При этом каждый слой делится на множество гиперколонок пронизывающих насквозь эти слои. Микроколонки кодируются цифрами и единицами с получением результата на выходе. Если требуется, то лишние слои и нейроны удаляются или добавляются. Идеально для подбора числа нейронов и слоёв использовать суперкомпьютер. Такая система позволяет нейронным сетям быть пластичной.
Прогнозирование
Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и/или каких-то существующих в настоящий момент факторов. Следует отметить, что прогнозирование возможно только тогда, когда предыдущие изменения действительно в какой-то степени предопределяют будущие. Например, прогнозирование котировок акций на основе котировок за прошлую неделю может оказаться успешным (а может и не оказаться), тогда как прогнозирование результатов завтрашней лотереи на основе данных за последние 50 лет почти наверняка не даст никаких результатов.
Аппроксимация
Нейронные сети могут аппроксимировать непрерывные функции. Доказана обобщённая аппроксимационная теорема[14]: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любуюнепрерывную функцию с некоторой наперёд заданной точностью. Это означает, что нелинейная характеристика нейрона может быть произвольной: от сигмоидальной до произвольного волнового пакета или вейвлета, синуса или многочлена. От выбора нелинейной функции может зависеть сложность конкретной сети, но с любой нелинейностью сеть остаётся универсальным аппроксиматором и при правильном выборе структуры может достаточно точно аппроксимировать функционирование любого непрерывного автомата.
Сжатие данных и Ассоциативная память
Способность нейросетей к выявлению взаимосвязей между различными параметрами дает возможность выразить данные большой размерности более компактно, если данные тесно взаимосвязаны друг с другом. Обратный процесс — восстановление исходного набора данных из части информации — называется (авто)ассоциативной памятью. Ассоциативная память позволяет также восстанавливать исходный сигнал/образ из зашумленных/поврежденных входных данных. Решение задачи гетероассоциативной памяти позволяет реализовать память, адресуемую по содержимому[13].
18. Источники напряжения и источники тока (эквивалентная схема источника напряжения, эквивалентная схема источника тока; расчет токов и мощности потребления: последовательно соединенная нагрузка, параллельно соединенная нагрузка).
Любое электронное устройство строится на основе электронных компонентов.
Прежде всего, это:
источники электрической энергии;
активные приборы (например, транзисторы и интегральные схемы);
диоды;
резисторы;
катушки индуктивности;
конденсаторы.
Источники электрической энергии представлены источниками напряжения и тока. Реальный источник напряжения можно описать эквивалентной схемой (см.рис. ниже, а), содержащей последовательно включенные источник электродвижущей силы (ЭДС) Е и внутреннюю резистивность Ri.
Эквивалентные схемы реального источника постоянного напряжения (а) и тока (б)
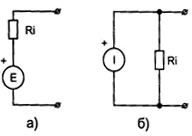
Сразу же отметим, что термин «резистивность» у нас не привился и многие предпочитают более привычный термин «сопротивление», так что Ri — внутреннее сопротивление. В тоже время «сопротивление», как деталь электронных схем, стали называть резистором.
Строго говоря, внутренне сопротивление — комплексная величина. Но пока мы ограничимся только действительными Ri, которые определяются как Ri = dU / dI, где dU — приращение напряжения на зажимах источника, а dI — приращение отбираемого от него тока. Ri может быть нелинейной величиной, зависящей от тока и даже отрицательной (приборы с падающей вольтамперной характеристикой — негатроны). В дальнейшем мы ограничимся представлением Ri, как сопротивления постоянного (линейного).
Самое широкое распространение, особенно при питании мобильной и малогабаритной электронной аппаратуры получили первичные источники постоянного напряжения — батареи из гальванических элементов и аккумуляторные батареи. Отдельный элемент таких батарей имеет ЭДС от 1,2 до 2,5 В при Riпорядка долей — единиц Ома. Широко применяются и всевозможные вторичные источники напряжения постоянного тока — от простых нестабилизированных выпрямителей до лабораторных источников питания с регулируемыми и высокостабильными напряжениями.
Реальный источник постоянного тока состоит из идеального источника тока I и параллельно включенного внутреннего сопротивления Ri (см.рис. выше,б). Первичные источники постоянного тока хотя и существуют, но широкого практического применения не нашли. Тем не менее, с возможностью их существования (как и с необходимостью измерения их параметров) надо считаться. Если внутреннее сопротивление источников постоянного напряжения обычно очень мало, то внутреннее сопротивление источников постоянного тока весьма велико и достигает десятков-сотен кОм, а порою — и единиц-десятков МОм. У идеального источника постоянного напряжения Ri=0, а у реального источника тока Ri=∞.
Характеристиками источников постоянного тока в некотором диапазоне напряжений обладают многие полупроводниковые приборы, например биполярные и полевые транзисторы. Выпускаются такжеспециальные микросхемы для стабилизации малых токов, например, микросхема стабилизатора постоянного тока КЖ101А, которая позволяет стабилизировать ток от десятков до сотен мкА в диапазоне напряжений от 1,8 В до 230 В. Значение Ri у нее составляет 8 МОм. Однако не следует путать устройства с большим динамическим дифференциальным сопротивлением с реальными первичными источниками постоянного тока. Первые всегда являются потребителями электрической энергии, тогда как вторые — ее источниками.
Измерение ЭДС первичных источников напряжения (например, аккумуляторов в начале и в конце заряда, или гальванической батареи после покупки или хранения) является довольно частой и довольно простой задачей. Как видно из измерительной схемы (см.рис. ниже), оно сводится просто к подключению вольтметра измерительной головкой V c входным сопротивлением Rвх к источнику напряжения.
Измерение ЭДС первичного источника напряжения постоянного тока
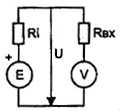
Учтите, что измерительная головка V на деле может быть измерителем тока, например, микроамперметром тестера.
Любые измерения возможны с некоторой погрешностью. Обычно у измерительных приборов задается основная и дополнительная погрешности. Основная погрешность определяется для некоторых идеализированных условий, например для пренебрежительно малого влияния температуры, отсутствия влияния внешних цепей и т.д. Дополнительная погрешность определяется при наличии влияния дополнительных факторов.
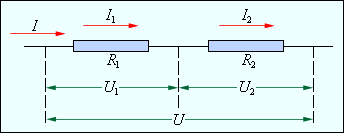
Проводники в электрических цепях могут соединяться последовательно и параллельно. При последовательном соединении проводников (рис. 4.9.1) сила тока во всех проводниках одинакова:
I1 = I2 = I. |
|
Рисунок 4.9.1. Последовательное соединение проводников. |
По закону Ома, напряжения U1 и U2 на проводниках равны
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
|
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников. При параллельном соединении (рис. 4.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
U1 = U2 = U. |
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I = I1 + I2. |
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
|
Рисунок 4.9.2. Параллельное соединение проводников. |
Записывая на основании закона Ома
|
где R – электрическое сопротивление всей цепи, получим
|
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. Этот результат справедлив для любого числа параллельно включенных проводников. Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 4.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
|
Рисунок 4.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом). |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 4.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
|
Рисунок 4.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников. |
Цепи, подобные изображенной на рис. 4.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.
Закон Ома для участка цепи
Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома
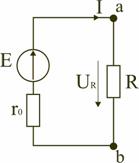 Рис.
1.3
Рис.
1.3
(1.1)
![]() или UR=RI.
или UR=RI.
В этом случае UR=RI – называют напряжением или падением напряжения на резисторе R, а – током в резисторе R.
При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:
![]() .
.
В этом случае закон Ома для участка цепи запишется в виде:
I=Ug.
Закон Ома для всей цепи
Этот закон определяет зависимость между ЭДС E источника питания с внутренним сопротивлением r0 (рис. 1.3), током I электрической цепи и общим эквивалентным сопротивлением RЭ=r0+R всей цепи:
(1.2)
 .
.
Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.
Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
(1.3)
![]() ,
,
где m – число ветвей подключенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I−I1−I2=0.
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
(1.4)
![]() ,
,
где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rk в контуре; Uk=RkIk – напряжение или падение напряжения на k-м элементе контура.
Для схемы (рис. 1.2) запишем уравнение по второму закону Кирхгофа:
E=UR+U1.
Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю
(1.5)
![]() .
.
При записи уравнений по второму закону Кирхгофа необходимо:
1) задать условные положительные направления ЭДС, токов и напряжений;
2) выбрать направление обхода контура, для которого записывается уравнение;
3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.
Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 1.2):
контур I: E=RI+R1I1+r0I,
контур II: R1I1+R2I2=0,
контур III: E=RI+R2I2+r0I.
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
(1.6)
W=I2Rt.
Скорость преобразования электрической энергии в другие виды представляет электрическую мощность
(1.7)
![]() .
.
Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.
(1.8)
![]() .
.
Это соотношение (1.8) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в (1.8) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение EI подставляют в (1.8) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:
EI=I2(r0+R)+I12R1+I22R2.
При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А), напряжение – в вольтах (В), сопротивление – в омах (Ом), мощность – в ваттах (Вт), электрическая энергия – ватт-час (Вт-час) и проводимость – в сименсах (См)
Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1 мA = 10–3 А), килоампер (1 кA = 103 А), милливольт (1 мВ = 10–3 В), киловольт (1 кВ = 103 В), килоом (1 кОм = 103 Ом), мегаом (1 МОм = 106 Ом), киловатт (1 кВт = 103 Вт), киловатт-час (1 кВт-час = 103 ватт-час).
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r0 заменяют расчетным эквивалентным источником ЭДС или источником тока.
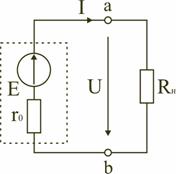 Рис.
1.14
Рис.
1.14
Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r0, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.
Для данной цепи запишем соотношение по второму закону Кирхгофа
(1.10)
E=U+Ir0 или E=U−Ir0.
Эта
зависимость напряжения U на
зажимах реального источника от
тока I определяется
его вольт-амперной или внешней
характеристикой (рис. 1.15). Уменьшение
напряжения источника U при
увеличении тока нагрузки I объясняется
падением напряжения ![]() на
его внутреннем сопротивлении r0.
на
его внутреннем сопротивлении r0.
|
|
Рис. 1.15 |
Рис. 1.16 |
У идеального источника ЭДС внутреннее сопротивление r0<<Rн (приближенно r0≈0). В этом случае его вольт-амперная характеристика представляет собой прямую линию (рис. 1.16), следовательно, напряжение U на его зажимах постоянно (U=E) и не зависит от величины сопротивления нагрузки Rн.
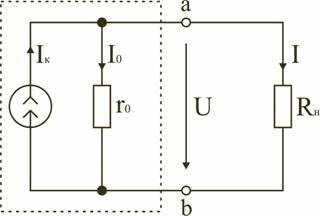 Рис.
1.17
Рис.
1.17
Источник
тока, заменяющий реальный источник
электрической энергии, характеризуется
неизменным по величине током Iк,
равным току короткого замыкания источника
ЭДС 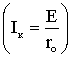 ,
и внутренним сопротивление r0,
включенным параллельно (рис. 1.17).
,
и внутренним сопротивление r0,
включенным параллельно (рис. 1.17).
Стрелка в кружке указывает положительное направление тока источника. Для данной цепи запишем соотношение по первому закону Кирхгофа
Iк=I0+I;  .
.
В этом случае вольт-амперная (внешняя) характеристика I(U) источника тока определится соотношением
(1.11)
I=Iк−I0=Iк−U/r0
и представлена на рис. 1.18.
|
|
Рис. 1.18 |
Рис. 1.19 |
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока I0, замыкающегося в цепи источника тока.
В идеальном источнике тока r0>>Rн. В этом случае можно считать, что при изменении сопротивления нагрузки Rн потребителя I0≈0, а I≈Iк. Тогда из выражения (1.11) следует, что вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I=Iк=E/r0 (рис. 1.19).
При сравнении внешних характеристик источника ЭДС (рис. 1.15) и источника тока (рис. 1.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.
Ток
в нагрузке Rн для
схем источника ЭДС (рис. 1.14) и источника
тока (рис. 1.17) одинаков и равен 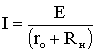 .
.
Для
схемы (рис. 1.14) это следует из закона
Ома, т.к. при последователь-ном соединении
сопротивления r0 и Rн складываются.
В схеме (рис. 1.17) ток 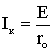 распределяется
обратно пропорционально
сопротивлениям r0 и Rн двух
параллельных ветвей. Ток в нагрузке Rн
распределяется
обратно пропорционально
сопротивлениям r0 и Rн двух
параллельных ветвей. Ток в нагрузке Rн
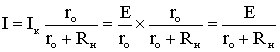 ,
,
т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 1.17) эквивалентна схеме источника ЭДС (рис. 1.14) в отношении энергии, выделяющейся в сопротивлении нагрузки Rн, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.
Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r0 и величиной электродвижущей силы E.
В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.
Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 1.20).
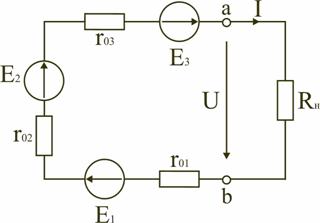
Рис. 1.20
Для этой цепи на основании второго закона Кирхгофа можно записать
E1+E2+E3=I(r01+r02+r03+Rн),
откуда
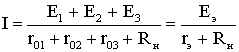 .
.
Таким образом, электрическая цепь на рис. 1.20 может быть заменена цепью с эквивалентным источником питания (рис. 1.21), имеющим ЭДС Eэ и внутреннее сопротивление rэ.
|
|
При параллельном соединении источников (рис. 1.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U на выводах всех источников. Для электрической цепи на рис. 1.22 можно записать следующие уравнения:
I=I1+I2+I3; P=P1+P2+P3=UI1+UI2+UI3=UI.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей. На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.
Расчет электрических цепей с использованием законов Ома и Кирхгофа
Законы Ома и Кирхгофа используют, как правило, при расчете относительно простых электрических цепей с небольшим числом контуров, хотя принципиально с их помощью можно рассчитать сколь угодно сложные электрические цепи.
При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Зная токи, можно найти напряжения на элементах цепи, мощность, потребляемую отдельными элементами и всей цепью в целом, мощность источников питания и др.
Расчет цепи с одним источником питания
Электрическая цепь, схема которой приведена на рис. 1.25, состоит из одного источника питания, имеющего ЭДС E и внутреннее сопротивление r0, и резисторов R1,R2,R3, подключенных к источнику по смешанной схеме. Операции расчета такой схемы рекомендуется производить в определенной последовательности.
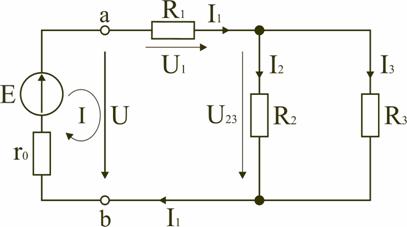
Рис. 1.25
1. Обозначение токов и напряжений на участках цепи.
Резистор R1 включен последовательно с источником, поэтому ток I1 для них будет общим, токи в резисторах R2 и R3 обозначим соответственно I2 и I3. Аналогично обозначим напряжения на участках цепи.
2. Расчет эквивалентного сопротивления цепи.
Резисторы R2 и R3 включены по параллельной схеме и заменяются согласно (1.7) эквивалентным сопротивлением:
![]() .
.
В результате цепь на рис. 1.25 преобразуется в цепь с последовательно соединенными резисторами R1,R23 и r0. Тогда эквивалентное сопротивление всей цепи запишется в виде:
Rэ=r0+R1+R23
3. Расчет тока в цепи источника. Ток I1 определим по закону Ома (1.2):
I1=U/Rэ
4. Расчет напряжений на участках цепи. По закону Ома (1.1) определим величины напряжений:
U1=I1R1; U23=I1R23
Напряжение U на зажимах ab источника питания определим по второму закону Кирхгофа (1.4) для контура I (рис. 1.25):
E=I1r0+U; U=E−I1r0.
5. Расчет токов и мощностей для всех участков цепи. Зная величину напряжения U23, определим по закону Ома токи в резисторах R2 и R3:
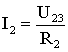 ;
;  .
.
По формуле (1.8) определим величину активной электрической мощности, отдаваемую источником питания потребителям электрической энергии:
P=EI1.
В элементах схемы расходуются активные мощности:
![]() ;
; ![]() ;
; ![]() .
.
На
внутреннем сопротивлении r0 источника
питания расходуется часть электрической
мощности, отдаваемой источником. Эту
мощность называют мощностью потерь ![]() :
:
![]() .
.
6. Проверка правильности расчетов. Эта проверка производится составлением уравнения баланса мощностей (1.8): мощность, отдаваемая источником питания, должна быть равна сумме мощностей, расходуемых в резистивных элементах схемы:
![]() .
.
Кроме того, правильность вычисления токов можно проверить, составив уравнение по первому закону Кирхгофа (1.3) для узла схемы:
I1=I2+I3.
Расчет разветвленной электрической цепи с несколькими источниками питания
Основным методом расчета является метод непосредственного применения первого и второго законов Кирхгофа.
В качестве примера рассмотрим цепь, схема которой приведена на рис. 1.26. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа (1.3) составляют уравнения для (n–1) узлов. Недостающиеm–(n–1) уравнения получают по второму закону Кирхгофа (1.4), составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.
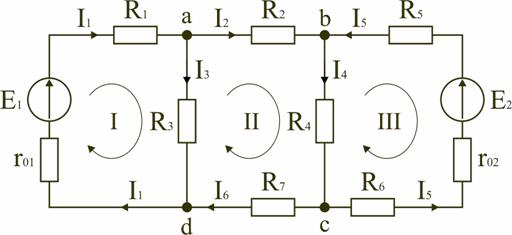
Рис. 1.26
1. Обозначение токов во всех ветвях. Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендеются, чтобы направление токов совпадало с направлением ЭДС.
2. Составление уравнений по первому закону Кирхгофа. Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения:
узел a: I1−I2−I3=0;
узел b: I2−I4+I5=0;
узел c: I4−I5+I6=0.
3. Составление уравнений по второму закону Кирхгофа. Необходимо составить 6–3=3 уравнения. В схеме на рис. 1.26 выбираем контура I, II, III и для них записываем уравнения:
контур I: E1=I1(r01+R1)+I3R3;
контур II: 0=I2R2+I4R4+I6R7−I3R3;
контур III: −E2=−I5(r02+R5+R6)−I4R4.
4. Решение полученной системы уравнений и анализ результатов. Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя.
5. Проверка правильности расчетов. Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений:
узел d: I3+I6−I1=0
внешний контур схемы: E1−E2=I1(r01+R1)+I2R2−I5(r02+R5+R6)+I6R7.
Независимой проверкой является составление уравнения баланса мощностей (1.8) с учетом режимов работы элементов схемы с ЭДС:
![]() .
.
Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.


 1
1 2
2 3
3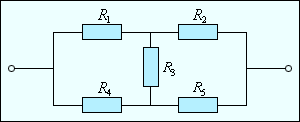 4
4
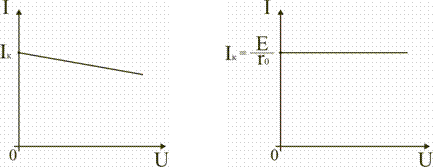
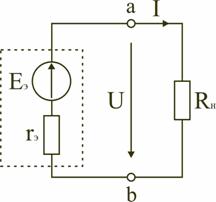 Рис.
1.21
Рис.
1.21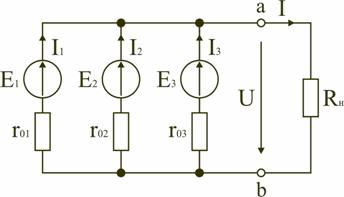 Рис.
1.22
Рис.
1.22