18. Динамические модели в экономике (регрессионные, авторегрессионные, регрессионно-авторегрессионные модели; модели накопления и дисконтирования; модели «затраты-выпуск»).

Динамические регрессионные модели позволяют учитывать причинные факторы, такие как цены и другие экономических показателей в ваших прогнозах. Динамические регрессионные модели – сочетание стандартных моделей регрессионных операций с возможностью использования динамических условиях, охватывающих тенденции, сезонность. В результате получается более точная модель.

Четко определенные динамической регрессионной модели позволяет понять взаимосвязь между переменными и допускает сценарии вида “что если”. К примеру, ваша модель динамической регрессии включает в себя стоимость по сути “объясняющую” переменную, количественной взаимосвязи между ценами продаж, модель же позволяет создавать различных ценовые сценарии. “Что, если мы поднимаем цену?”, “Что, если мы ее снизим?”. Генерация полного набора таких альтернативных сценариев может помочь вам определить эффективную ценовую стратегию.

Четко определенные динамические модели регрессии отражает связь между зависимой переменной и одной или несколькими независимыми переменными. Если эти независимые переменные находятся под вашим контролем (например, цены, рекламные акции и т.д.), или, если они ведут показателей это может оказаться серьезной проблемой.

Большинство методов прогнозирования могут быть в значительной степени автоматизированы экспертной системой (например Forecast Pro), которая выполняет различные статистические тесты, а затем выбирает и строит окончательную модель.

Для многих процессов в экономике характерно наличие связи между значениями исследуемого показателя в предпрогнозном и прогнозном периодах. Зависимость от времени проявляется в данном случае через характеристики внутренней структуры процесса в предшествующем периоде.

Уравнение, выражающее величину переменной yt в момент t через значения этой переменной в моменты (t -\),(t ~2),...,(t-р), называется уравнением авторегрессии. В линейной форме уравнение имеет вид:

Уг = «1^-1 + «2^-2 + • • • + aPyt-P + et> (4-24)

где st - случайная составляющая с нулевым математическим ожиданием и дисперсией сг? .

Применение авторегрессионных моделей основано на предварительном экономическом анализе, когда известно, что изучаемый процесс в значительной степени зависит от его развития в прошлые периоды. В некоторых случаях они используются для нахождения простого преобразования, приводящего к последовательности независимых случайных величин.

Существует другое определение авторегрессионной модели: модель стационарного процесса, выражающего значение показателя в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей.

В процессе анализа реальных экономических явлений понятие стационарности может быть лишь удобной абстракцией для применения статистических моделей.

Количество уровней, включенных в правую часть уравнения авторегрессии, определяет порядок уравнения.

Для предварительного изучения особенностей автокорреляционного взаимодействия элементов ряда целесообразно проводить графический анализ исходных данных путем нанесения на координатные поля пар значений (У,,У,-МУ{>У{-2\->(У,,У,-Р)- Интервалы времени (t,i -k),k = 1,2,3,...,р, характеризующие удаленность сопоставляемых уровней ряда друг от друга, называются периодом запаздывания. Он показывает, через какой промежуток времени изменение переменной yt_k окажет воздей- ствие на yt. Изучение графических построений для различных к позволяет приближенно оценить направление и силу связи между близлежащими членами ряда.

Для оценки тесноты связи используется коэффициент автокорреляции, определяемый по формуле:

ск

г к=-*-, где

со

2 п-к ^ п

П t=1 п t=l

Определив гк для нескольких интервалов запаздывания в диапазоне 1 < к < п / 4 , можно получить так называемую автокорреляционную функцию, показывающую, как изменяется коэффициент автокорреляции по мере увеличения расстояния между сопоставляемыми уровнями временного ряда.

Автокорреляционная функция характеризуется тенденцией к затуханию колебаний, т.е. уменьшению абсолютной величины коэффициента. Вследствие этого для ее анализа используются такие характеристики, как период колебаний, частота колебаний, амплитуда колебаний, фаза, т.е угловая величина отклонения автокорреляционной функции от нулевого состояния.

Оценка параметров уравнений авторегрессии выполняется методом наименьших квадратов. Прогнозирование на основе авторегрессионной модели представляет многоэтапную процедуру, каждая стадия которой позволяет определить величину показателя на очередной единичный отрезок времени.

В качестве простейшего критерия адекватности уравнения авторегрессии исходному временному ряду может использоваться показатель абсолютного среднего отклонения, определяемый по формуле:

Z к-яI

= . , . (4.25)

n-p-l + l

Сферой применения моделей авторегрессии является моделирование спроса на предметы текущего потребления, изменение складских запасов и другие составляющие логистических процессов.

В условиях инфляции очевидно, что деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги, являются операции накопления (наращивания) и дисконтирования.

Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости, при условии, что вложенная сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент.

Дисконтирование – это процесс приведения денежных поступлений от инвестиций к их текущей стоимости.

В оценке эти финансовые расчеты базируются на сложном процессе, когда каждое последующее начисление ставки процента осуществляется как на основную сумму, так и на начисленные за предыдущие периоды невыплаченные проценты.

Результат определяется используемыми данными, качеством информационного поля. Подобно всем математическим моделям модель дисконтированных будущих доходов хороша настолько, насколько хороши используемые в ней данные; она даст правильный ответ для любого вида вводных. Соответственно вопрос заключается в том, насколько корректны введенные данные, давшие такой ответ. Для инвестиционных решений, связанных с крупными вложениями капитала, лучше получить ответ правильный в приближении, чем заведомо неверный. При неверном использовании модель дисконтированных будущих доходов даст именно это: точный, однако совершенно неверный ответ.

Классической моделью, позволяющей описывать внутреннюю структуру производства (технологии), а так же взаимосвязь ресурсов и готовой продукции, является модель В.В. Леонтьева "затраты – выпуск". В ней ключевыми характеристиками технологий, определяющими зависимости выпуска продукции и затрат производственных ресурсов служат коэффициенты прямых затрат (технологические коэффициенты). Метод анализа модели сводится к решению системы соответствующих линейных уравнений, устанавливающих баланс между используемыми технологиями, выпуском продукции и затратами факторов производства. это метод систематической квантификации количественных взаимосвязей между различными секторами сложной экономической системы. С помощью этого метода можно анализировать любую экономическую систему: макросистему - народное хозяйство в целом, мегасистему - мировое хозяйство как совокупность экономических взаимосвязей, промежуточную - региональную экономику отдельных материков, микросистему - экономику отдельного административного штата, области, района, предприятия. Но в любом случае подход в основном один и тот же

Модель «Затраты-выпуск»

Модель экономической системы «Затраты-выпуск» может быть описана следующей системой уравнений [9]:QВЫХ = W1(p) (μ – QЗАК); (6.25)

μ = η (t – τ);

η = W2(p) ε +W3(p) QЗАК;

ε = QЗАД — QВЫХ,

где η — приказы, издаваемые в момент времени t; μ — скорость выпуска готовой продукции; ε — запасы (дефицит); τ — запаздывание выпуска продукции; QЗАД, QВЫХ, QЗАК – соответственно заданная, действительная и поступающая (требование рынка) величина запасов; W1(p) = 1/р – передаточная функция поступления продукции на склад; W2(p), W3(p) – передаточные функции (законы управления), соответствующие принятию решений соответственно отделами менеджмента и маркетинга.

Анализируя приведенную систему уравнений, можно сделать вывод, что она не имеет однозначного решения (нелинейное уравнение). Поэтому целесообразно применение имитационного моделирования с применением ЦВМ.

Уравнениям (6.25) соответствует структурная схема, представленная на рис. 6.13.

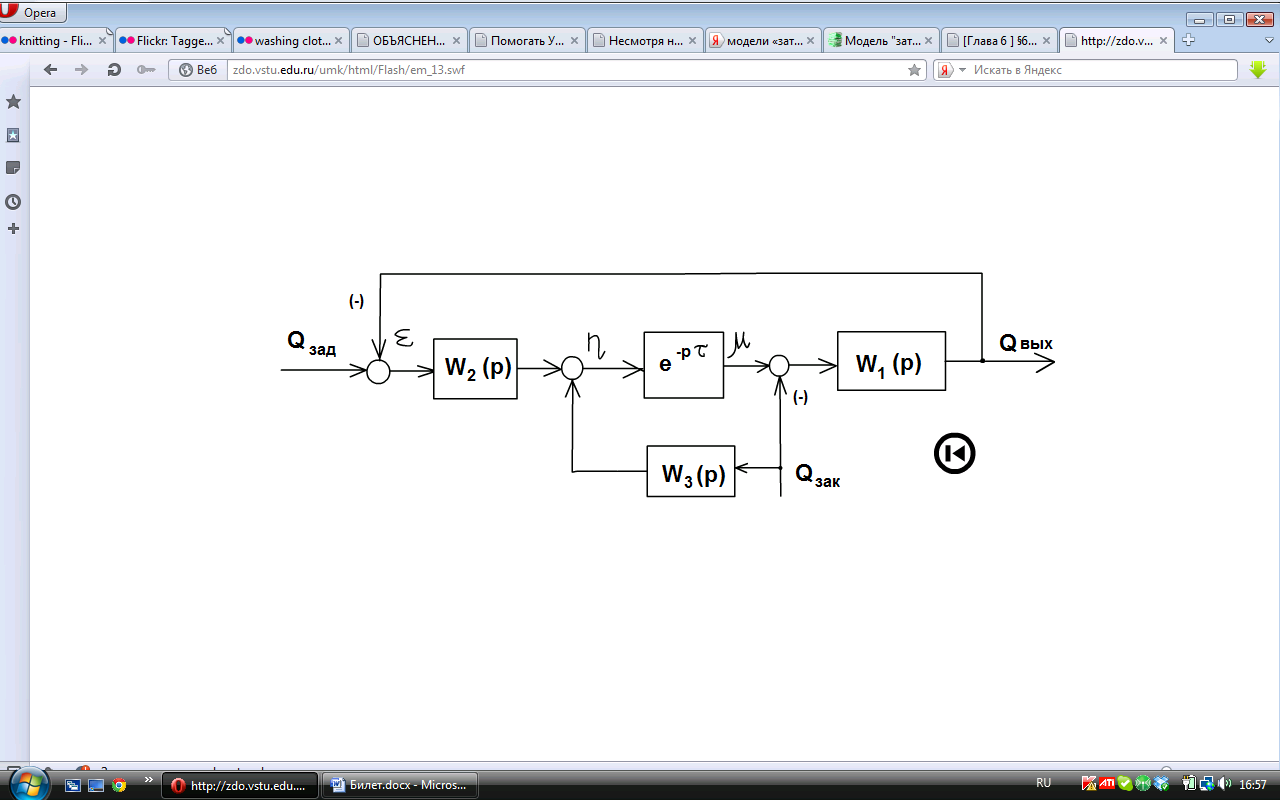
Приведенная система (6.25) регулирования запасов с точки зрения имитационного моделирования интересна тем, что регулирование запасов не является тривиальной задачей. И здесь важно найти такую функцию реального принятия решения W3(p) (отдел маркетинга), связанной с новыми поступлениями заказов, чтобы стабилизация их была совершенной (оптимальной). В структурной схеме рис. 6.13 менеджмент участвует в замкнутом контуре системы регулирования запасов и от его действий (законов управления) также зависит оптимизация складских запасов.

Большие запасы порождают затраты по уплате процентов, а также, возможно, издержки физического обесценивания при хранении, складские затраты и т.д. С другой стороны, нехватка запасов (избыточные отрицательные запасы) вызывает затраты в смысле задержки в выполнении заказов, а следовательно, недоброжелательное отношение заказчиков. Разумно предположить (потребовать при моделировании), что издержки производства определенного количества продукции за некоторый промежуток времени будут минимальными при постоянном выпуске продукции.

Имитационное моделирование приведенной экономической системы предполагает формулирование выводов (интерпретация полученных зависимостей) по полученным результатам (переходным процессам) воздействия на систему различных (реальных статистических) возмущающих (QЗАК) и управляющих (QЗАД) воздействиях. Не стоит забывать, что интуитивные выводы в этом случае дополняются точностью математических методов.

18. Параметрические и непараметрические векторные зависимости (параметрические зависимости одной величины от совокупности других величин; непараметрические зависимости одной величины от совокупности других величин).

Корреля́ция(от лат. correlatio), (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение  ^[2], либо коэффициент корреляции   (или  )^[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.^[5]В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи.

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

где   — вектор неизвестных параметров модели

 — случайная ошибка модели.

Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть   — номер наблюдения ( ). Тогда   — значения переменных в  -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:

Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков   (англ. Residual Sum of Squares^[1]) будет минимальной:

где:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции  , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:

Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).

Корреляционные параметрические методы - методы оценки тесноты свози, основанные на использовании, как правило, оценок нормального распределения, применяются в тех случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения.

Параметризация уравнения регрессии: установление формы зависимости; определение функции регрессии; оценка значений параметров выбранной формулы статистической связи Методы изучения связи - форму зависимости можно установить с помощью поля корреляции. Если исходные данные (значения переменных х и у) нанести на график в виде точек в прямоугольной системе координат, то получимполе корреляции При этом значения независимой переменной x (признак-фактор) откладываются по оси абсцисс, а значения результирующего фактора у откладываются по оси ординат. Если зависимость у от xфункциональная, то все точки расположены на какой-то линии. При корреляционной связи вследствие влияния прочих факторов точки не лежат на одной линии.

Расчет показателей силы и тесноты связей Линейный коэффициент корреляции - количественная оценка и мера тесноты связи двух переменных. Коэффициент корреляции принимает значения в интервале от -1 до +1. Считают, что если этот коэффициент не больше 0,30, то связь слабая: от 0,3 до 0,7 - средняя; больше 0,7 - сильная, или тесная. Когда коэффициент равен 1, то связь функциональная, если он равен 0, то говорят об отсутствии линейной связи между признаками.

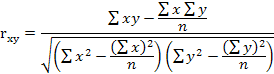
Коэффициент детерминации - квадрат линейного коэффициента корреляции, рассчитываемый для оценки качества подбора линейной функции.

Формула нелинейного коэффициента корреляции:

Корреляция для нелинейной регрессии Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно - индексом корреляции (R):

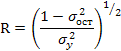
где  - общая дисперсия результативного признака у,   - остаточная дисперсия, определяемая исходя из уравнения регрессии : ух = f (х). Корреляция для множественной регрессии. Значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата - коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оце­нивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

где   - общая дисперсия результативного признака;

 - остаточная дисперсия для уравнения

у = f (x₁,x₂,…,x_p)

Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является простота вычислений.

Непараметрические показатели связи

Коэффициент ассоциации:

Коэффициент контингенции:

Коэффициент взаимной сопряженности Пирсона:

     

Коэффициент Фехнера:

Коэффициент корреляции рангов:

Непараметрические показатели связи позволяет судить о степени и тесноте связи не только, для количественных, но и для атрибутивных признаков.

Методы многомерного анализа, основанные на рассмотрении сочетания непараметрических взаимосвязанных признаков:

1) дискриминантный анализ состоит в установлении правила, на основании которого та или иная новая единица не может быть отнесена к данной совокупности объектов, имея в виду значения рассматриваемых у нее признаков;

2) распознавание образов состоит в отнесении объекта на основании сочетания признаков в ту или другую из заранее определенных и охарактеризованных групп совокупности;

3) кластерный анализ (таксономия) состоит в разбиении совокупности на классы (группы, типы, «кластеры», «таксоны»), границы которых наперед не заданы. Число кластеров может быть при этом задано или нет;

4) метод главных компонент - если признаки отобраны правильной в них действительно отражается качественная природа объектов в рассматриваемом отношении, то эти признаки оказываются друг с другом связанными;

факторный анализ является дальнейшим развитием метода главных компонент. В нем охватываемая выделенными -главными компонентами» У вариация всех признаков X может затем между ними перераспределяться, причем между ними может быть допущена и корреляция.

Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.

Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили названиенепараметрических.

Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемыхтаблиц взаимной сопряженности.

Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.

Занятия родителей	Число детей, занятых в				Всего
	Промышлен- ности и стро- ительстве	сельском  хозяйстве	сфере  обслужи- вания	сфере интел- лектуального  труда
1. Промышленность и строительство 2. Сельское хозяйство 3. Сфера обслуживания 4. Сфера интеллектульного труда	40 34 16 24	5 29 6 5	7 13 15 9	39 12 19 72		91 88 56 110
Всего	114	45	44	142		345

Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.

Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.

Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):

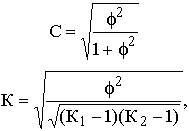
где f² – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:

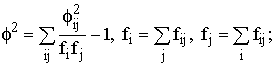
К₁ и К₂ – число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.

В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.

При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.

Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.