
- •Основы информационных технологий (теория систем, дискретная и компьютерная математика, теория управления, моделирование) (Первые вопросы в билетах).
- •Интерполирование функций (многочленами Лагранжа; интерполяционная формула Ньютона; интерполяция кубическими сплайнами).
- •Приближение функций (метод наименьших квадратов; линейная регрессия; нелинейная регрессия; полиномиальная аппроксимация; дискретное преобразование Фурье).
- •Формула трапеций
- •Численное решение систем линейных алгебраических уравнений (метод Гаусса; метод итераций).
- •11. Универсальный метод информационных технологий – статистическое моделирование нелинейных систем со случайными характеристиками в условиях помех (метод Монте-Карло).
- •!!!13 И 14 вопросы отсутствуют в билетах!!!
- •!!!16 Вопрос отсутствует в билетах!!!
- •1.2.1. Принцип разомкнутого управления
- •1.2.2. Принцип компенсации
- •1.2.3. Принцип обратной связи
- •1. Введение
- •2. Итерационные методы Якоби и Зейделя
- •3. Метод последовательной верхней релаксации
- •4. Матрично-векторное представление итерационных методов
- •Динамические модели в экономике (регрессионные, авторегрессионные, регрессионно-авторегрессионные модели; модели накопления и дисконтирования; модели «затраты-выпуск»).
- •Основы вычислительной техники. (Вторые вопросы в билетах)
- •Характеристики современных операционных систем (многопоточность, симметричная многопроцессорность, распределенные операционные системы, объектно-ориентированный дизайн).
- •Дискретный сигнал
- •Вычислительные сети и системы (протоколы обмена тср, iр, ssl, skip, NetBeui, ipx, spx, NetBios, модель osi, типы соединения эвм, используемые при построении локальных сетей).
- •Информация (аналоговая и цифровая информация, оценки количества информации, энтропийный подход).
- •Структура микропроцессора (алу, регистры: аккумуляторы, ввода-вывода, понятие шины: шина данных, адресная шина, шина команд; запоминающие устройства: пзу, озу, созу, кэш-память).
- •!!!16 Вопроса нет в билетах!!!
- •17. Понятие нелинейных преобразователей (транзисторы, ключи, диодные выпрямители, логические элементы, нейронные сети).
- •1.8. Основные методы расчета сложных электрических цепей
- •19. Расчет комплексных сопротивлений линейных цепей (последовательные цепи: rc-цепь, rl-цепь, rlc-цепь; параллельные цепи: rc-цепь, rl-цепь, lc-цепь; последовательно-параллельные цепи: r-lc, c-rl).
- •Основы алгоритмизации и программирования. (Третьи вопросы в билетах)
- •2. Методы сортировки и поиска данных в массивах и файлах. Оценки скорости.
- •Современные языки программирования (с, Java, Delphi, vb). Типы данных языка. Структура приложения.
- •Примитивные типы
- •Типы данных
- •Объекты
- •Статическая и динамическая память, определение, область применения. Алгоритмы обработки очереди, списка, стека.
- •4 Шага добавления
- •Основные компоненты в языках (с, Java, Delphi). Их свойства, методы, события. Реализация графики.
- •7. Понятия объектно-ориентированного программирования. Поля, свойства, методы, события. Область видимости. Пример класса.
- •Базы данных. Типы бд. Реляционные бд. Типы полей. Типы связей. Язык запросов sql. Индексирование баз данных.
- •Создание Internet-приложений (на стороне клиента и сервера). Язык разметки гипертекста html. Специализированные инструменты (php). Создание Internet-приложений средствами языков с, Java, Delphi.
- •Глава 1 – содержание элемента html
- •6.3. Рисунки
- •Основные элементы блок схем программирования, типовые блок схемы (ввода-вывода, исполнения команд, условного перехода; ветвящиеся программы, циклические программы, вложенные циклы).
3. Метод последовательной верхней релаксации
Метод последовательной верхней релаксации (ПВР) основан на линейной экстраполяции по двум итерационным шагам метода Зейделя. Новое значение каждого компонента вектора неизвестных X вычисляется по формуле:
 (6)
(6)
где
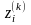 -
значение i-того компонента вектора
,
получаемое на k-том итерационном шаге
методом Зейделя (т.е. по формуле (5);
-
значение i-того компонента вектора
,
получаемое на k-том итерационном шаге
методом Зейделя (т.е. по формуле (5);
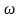 -
релаксационный параметр, регулирующий
сходимость.
-
релаксационный параметр, регулирующий
сходимость.
Для
матриц, встречающихся в задачах
моделирования физических процессов
(симметричных, положительно определенных
с диагональным преобладанием, см. / 2 /),
его значение может лежать в диапазоне
от 0 до 2. При
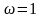 метод
ПВР превращается в метод Зейделя. Для
каждого типа матриц можно подобрать
оптимальное значение параметра
,
позволяющее получить решение при
минимальном числе итераций.
метод
ПВР превращается в метод Зейделя. Для
каждого типа матриц можно подобрать
оптимальное значение параметра
,
позволяющее получить решение при
минимальном числе итераций.
4. Матрично-векторное представление итерационных методов
В современных алгоритмах используется более красивое представление итерационных формул метода Якоби и Зейделя, основанное на векторно-матричной записи. Сначала матрица коэффициентов СЛАУ представляется в виде трех слагаемых:
 ,
(7)
,
(7)
где A1 - нижняя треугольная матрица, D - диагональная матрица, A2- верхняя треугольная матрица.
Например,
матрица
 раскладывается следующим образом:
раскладывается следующим образом:
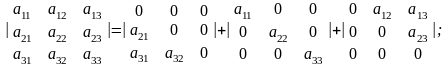
Несложные преобразования, приведенные в / 2 /, позволяют получить:
для метода Якоби:
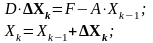 (8)
(8)
для метода Зейделя:
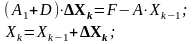 (9)
(9)
Итерационные
формулы состоят из двух частей: первая
представляет собой СЛАУ, которую на
каждой итерации нужно решить относительно
 ,
а вторая - итерационный шаг. Решение
СЛАУ проблемы не представляет, так как
в первом случае матрица - диагональная,
а во втором - нижняя треугольная.
,
а вторая - итерационный шаг. Решение
СЛАУ проблемы не представляет, так как
в первом случае матрица - диагональная,
а во втором - нижняя треугольная.
Метод ПВР в матрично-векторной форме принимает вид:
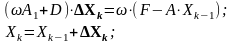 (10)
(10)
Метрические и неметрические меры сходства многомерных данных (евклидово и гильбертово пространство, основные аксиомы треугольника; корреляционные меры сходства, понятие оптимальных по различению мер сходства; сравнение частотных распределений – критерий хи-квадрат, применение критерия для проверки гипотез о статистической зависимости факторов).
Евклидово пространство
1) Пространство, свойства которого описываются аксиомами евклидовой геометрии.
2)
Векторное пространство E
над полем R
действительных чисел, в котором каждой
паре векторов x
и y
из E
ставится в соответствие действительное
число (называемое скалярным произведением
(x,
y)
этих векторов). Через скалярное
произведение в евклидовом пространстве
определяются длина |x|
вектора x
и угол
![]() между векторами x
и y:
между векторами x
и y:

а также вводится понятие ортогональности: ортогональными считаются векторы, если их скалярное произведение равно 0.
Примеры евклидовых пространств:
1) Множество всех векторов плоскости или трёхмерного пространства элементарной евклидовой геометрии с обычным скалярным произведением.
2) Конечномерное векторное пространство над R, в котором скалярное произведение векторов x = (x1, x2, ..., xn) и y = (y1, y2, ..., yn) определено формулой
(x, y) = x1y1 + x2y2 + ... + xnyn
(евклидово n-мерное арифметическое пространство).
Любые два евклидовых пространства одной и той же размерности изоморфны, т. е. существует изоморфизм соответствующих векторных пространств над R, сохраняющий скалярное произведение.
Бесконечномерное евклидово пространство обычно называют предгильбертовым пространством.
Гильбертово пространство, математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. Возникло на рубеже 19 и 20 вв. в виде естественного логического
вывода
из работ нем. математика Гильберта в
результате обобщения фактов и методов,
относящихся к разложениям функций в
ортогональные ряды и к исследованию
интегральных уравнений. Постепенно
развиваясь, понятие «Гильбертово
пространство»
находило все более широкие приложения
в различных разделах математики и
теоретической физики; оно принадлежит
к числу важнейших понятии математики.
Первоначально Гильбертово
пространство понималось
как пространство последовательностей
со сходящимся рядом квадратов (т. н.
пространство l2).
Элементами (векторами) такого
пространства являются бесконечные
числовые последовательности
x
= (x1,
x2,...,
xn,...)
такие, что ряд x21 +
x22 +...
+ х2n + ... сходится.
Сумму двух векторов х
+ y и
вектор lx,
где l -
действительное число, определяют
естественным образом:
x + y = (x1 +
y1,...,
xn +
yn,...),
lx = (lx1,
lx2,
..., lxn,...)/
Для любых векторов х,
y Î l2 формула
(x, y) = x1y1 +
x2y2 +
... +xnyn +
...
определяет их скалярное произведение,
а под длиной (нормой) вектора х понимается
неотрицательное число
|
Метрическое
пространство есть упорядоченная
пара ![]() ,
где
,
где ![]() —
множество элементов (точек) произвольной
природы, а
—
множество элементов (точек) произвольной
природы, а ![]() —
числовая функция, которая определена
на декартовом произведении
—
числовая функция, которая определена
на декартовом произведении ![]() ,
принимает значения в множестве
вещественных чисел и удовлетворяет
следующим трём аксиомам[1]:
,
принимает значения в множестве
вещественных чисел и удовлетворяет
следующим трём аксиомам[1]:
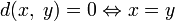 (аксиома
тождества).
(аксиома
тождества).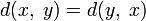 (аксиома
симметрии).
(аксиома
симметрии).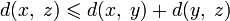 (аксиома
треугольника или неравенство
треугольника).
(аксиома
треугольника или неравенство
треугольника).
Функция ![]() ,
удовлетворяющая трём указанным аксиомам
называется метрикой.
,
удовлетворяющая трём указанным аксиомам
называется метрикой.
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях.
Аксиома 1: Существуют три точки не лежащие на одном отрезке.
Аксиома 2: Если прямая пересекает сторону треугольника и не проходит через его вершину, то она пересекает и другую сторону.
Будем
считать, что изображение эталонного
фрагмента (выбранного на снимке A и
представляемого матрицей ![]() размером
размером ![]() ),
сравнивается с изображениями фрагментов
снимка B в «зоне поиска»
),
сравнивается с изображениями фрагментов
снимка B в «зоне поиска» ![]() размером
размером ![]() .
Перекрытие между фрагментами определяется
шагом
.
Перекрытие между фрагментами определяется
шагом ![]() дискретной
решетки
дискретной
решетки ![]() (в
плоскости
(в
плоскости ![]() ),
на которой заданы наблюдаемые
переменные
),
на которой заданы наблюдаемые
переменные ![]() на
A или
на
A или ![]() на
B. В процессе скользящего поиска (когда
каждый очередной фрагмент получается
из предыдущего простым сдвигом на один
дискрет) вычисляется «функция сходства»
между изображением эталонного
фрагмента
на
B. В процессе скользящего поиска (когда
каждый очередной фрагмент получается
из предыдущего простым сдвигом на один
дискрет) вычисляется «функция сходства»
между изображением эталонного
фрагмента ![]() и
изображениями текущих (контролируемых)
фрагментов
и
изображениями текущих (контролируемых)
фрагментов ![]() .
Здесь требуется найти функцию сходства,
которая бы с максимально возможной
точностью и достоверностью позволяла
локализовать фрагмент, соответствующий
изображению эталонного фрагмента,
фиксируя таким образом сопряженные
точки на снимках.
.
Здесь требуется найти функцию сходства,
которая бы с максимально возможной
точностью и достоверностью позволяла
локализовать фрагмент, соответствующий
изображению эталонного фрагмента,
фиксируя таким образом сопряженные
точки на снимках.
Взаимно соответствующие элементы изображений одного объекта на снимках должны, очевидно, удовлетворять соотношению
![]() (5.25)
(5.25)
где ![]() и
и ![]() -
параметры контраста и средней
освещенности;
-
параметры контраста и средней
освещенности; ![]() ,
, ![]() -
параметры относительного сдвига образца
и его аналога на контролируемом снимке;
-
параметры относительного сдвига образца
и его аналога на контролируемом снимке; ![]() -
шум;
-
шум;
![]()
В такой формулировке процедура селекции образца должна найти параметры и , характеризующие сдвиг реперных фрагментов.
Ради простоты будем считать, что параметр не меняется по полю снимков, что позволяет перейти к центрированным переменным

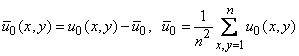 .
.
В
качестве меры различия в точке ![]() будем
брать среднеквадратичную ошибку
будем
брать среднеквадратичную ошибку
![]() (5.26)
(5.26)
которая
минимизируется перебором всех допускаемых
сдвигов эталона по заданной области
контролируемого снимка. Считается, что
в точке экстремума реализуется сходство,
если ![]() ,
где
,
где ![]() -
некоторый установленный порог. Из
требования минимума ошибки
-
некоторый установленный порог. Из
требования минимума ошибки ![]() находим
оценку
,
подставляем ее в формулу (5.26) и приходим
к выражению
находим
оценку
,
подставляем ее в формулу (5.26) и приходим
к выражению
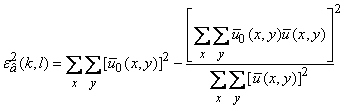 .
(5.27)
.
(5.27)
Первый член выражения (5.27) - «энергия» эталонного сигнала, является величиной постоянной, не зависящей от параметров сдвига . Поэтому точка экстремума не изменится, если мы нормируем среднеквадратичную ошибку к энергии эталона
 ,
,
и вместо минимума нормированной среднеквадратичной ошибки будем искать максимум коэффициента корреляции текущего фрагмента с эталоном
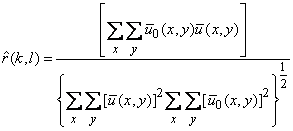 .
(5.28)
.
(5.28)
Соблюдение
условий достоверности обнаружения
также приводит к необходимости
установления порога для величины
взаимной корреляции ![]() :
если
:
если ![]() ,
то с заданной вероятностью гарантируется
действительное сходство найденной пары
фрагментов. Величина порога определяется
функцией распределения коэффициента
корреляции (при случайных выборках) и
задаваемой доверительной вероятностью
принятия решения о действительном
сходстве фрагментов.
,
то с заданной вероятностью гарантируется
действительное сходство найденной пары
фрагментов. Величина порога определяется
функцией распределения коэффициента
корреляции (при случайных выборках) и
задаваемой доверительной вероятностью
принятия решения о действительном
сходстве фрагментов.
Функционирование
данного (по существу классического)
алгоритма при наличии искажений в
изображениях рассмотрено в работе
[5.9]. Различия между эталонным и текущим
(![]() )
изображениями были обусловлены аддитивным
шумом и геометрическими искажениями,
которые моделировались аффинными
преобразованиями координат изображений:
)
изображениями были обусловлены аддитивным
шумом и геометрическими искажениями,
которые моделировались аффинными
преобразованиями координат изображений: ![]() ,
где
,
где ![]() ;
; ![]() -
матрица относительного поворота
изображений на угол
-
матрица относительного поворота
изображений на угол ![]() ;
; ![]() -
коэффициент изменения масштаба. В работе
показано, что среднее значение основного
пика корреляционной функции геометрически
искаженных изображений, нормированное
к средней величине пика при отсутствии
искажений, зависит от интенсивности
искажений и при малых
и
-
коэффициент изменения масштаба. В работе
показано, что среднее значение основного
пика корреляционной функции геометрически
искаженных изображений, нормированное
к средней величине пика при отсутствии
искажений, зависит от интенсивности
искажений и при малых
и ![]() имеет
вид
имеет
вид
![]()
Было практически продемонстрировано, что серьезным недостатком корреляционной меры сходства является ее чувствительность к геометрическим искажениям видимых размеров сопряженных фрагментов при изменении ракурса съемки.
Обычно в качестве критериев эффективности процедур идентификации сходства принимается точность совмещения фрагментов и вероятность ложной привязки, когда экстремум функционала сходства значимо смещен относительно истинного положения. Анализ результатов имитационных экспериментов позволил сделать следующие выводы .
1. При наличии геометрических искажений существует оптимальный размер фрагмента эталонного изображения, позволяющий минимизировать вероятность ложной привязки. Оптимальный размер фрагмента пропорционален эффективному радиусу корреляции (полуширине графика автокорреляционной функции) и уменьшается с увеличением геометрических искажений.
2. При заданном уровне искажений размер эталонного изображения, при котором погрешность совмещения минимальна, меньше, чем размер изображения, необходимый для минимизации вероятности ложной привязки.
Здесь можно порекомендовать использовать полезную модификацию метода идентификации сходства, заключающуюся в том, что искажения геометрии на втором снимке (относительно первого) предварительно компенсируются аффинной (или полиномиальной) "подгонкой". Например, параметры аффинного преобразования
![]() =
= ![]() ,
, ![]() ,
,
можно
оценивать адаптивно (в несколько
"проходов"), когда на первом этапе
задается достаточно большая зона
поиска по образцу, что позволяет на
искаженном (по отношению к исходному)
снимке находить сопряженные точки. Даже
трех пар опорных точек достаточно, чтобы
оценить (в первом приближении)
параметры аффинного преобразования и
осуществить аффинную подгонку геометрии
изображения ![]() к
геометрии изображения
к
геометрии изображения ![]()
![]() .
Это дает возможность повторным просмотром
найти уже существенно большее число
пар сопряженных точек на исходном
.
Это дает возможность повторным просмотром
найти уже существенно большее число
пар сопряженных точек на исходном ![]() и
аффинно-преобразованном
и
аффинно-преобразованном ![]() снимках
и уточнить по ним параметры
аффинной аппроксимации. Дальнейшее
повторение этой процедуры позволяет,
в принципе, идентифицировать любое
(допустимое данной аппроксимацией)
число пар сопряженных точек и,
следовательно, добиться заданной
точности в оценивании параметров
геометрического преобразования.
снимках
и уточнить по ним параметры
аффинной аппроксимации. Дальнейшее
повторение этой процедуры позволяет,
в принципе, идентифицировать любое
(допустимое данной аппроксимацией)
число пар сопряженных точек и,
следовательно, добиться заданной
точности в оценивании параметров
геометрического преобразования.
Поиск по образцу в данном методе сводится к вычислению нормированной взаимной корреляции распределения яркости (двумерного сигнала) на текущем фрагменте первого снимка с распределениями яркостей фрагментов, лежащих в некоторой предполагаемой окрестности образа этого фрагмента на аффинно-преобразованном втором снимке и определению целочисленных параметров взаимного смещения исходного фрагмента и его образа, устанавливаемого по экстремуму корреляционного функционала.
Критерием для определения схожести и различия кластеров является расстояние между точками на диаграмме рассеивания. Это сходство можно "измерить", оно равно расстоянию между точками на графике. Способов определения меры расстояния между кластерами, называемой еще мерой близости, существует несколько. Наиболее распространенный способ - вычисление евклидова расстояния между двумя точками i и j на плоскости, когда известны их координаты X и Y:
![]()
(13.1)
Примечание: чтобы узнать расстояние между двумя точками, надо взять разницу их координат по каждой оси, возвести ее в квадрат, сложить полученные значения для всех осей и извлечь квадратный корень из суммы.
Когда осей больше, чем две, расстояние рассчитывается таким образом: сумма квадратов разницы координат состоит из стольких слагаемых, сколько осей (измерений) присутствует в нашем пространстве. Например, если нам нужно найти расстояние между двумя точками в пространстве трех измерений, формула (13.1) приобретает вид:
![]()
(13.2)
Для вычисления расстояния между объектами используются различные меры сходства (меры подобия), называемые также метриками или функциями расстояний.
Квадрат евклидова расстояния.
Для придания больших весов более отдаленным друг от друга объектам можем воспользоваться квадратом евклидова расстояния путем возведения в квадрат стандартного евклидова расстояния.
Манхэттенское расстояние (расстояние городских кварталов), также называемое "хэмминговым" или "сити-блок" расстоянием.
Это расстояние рассчитывается как среднее разностей по координатам. В большинстве случаев эта мера расстояния приводит к результатам, подобным расчетам расстояния евклида. Однако, для этой меры влияние отдельных выбросов меньше, чем при использовании евклидова расстояния, поскольку здесь координаты не возводятся в квадрат.
Расстояние Чебышева. Это расстояние стоит использовать, когда необходимо определить два объекта как "различные", если они отличаются по какому-то одному измерению.
Процент несогласия. Это расстояние вычисляется, если данные являются категориальными.
Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
Обозначим
через X исследуемую случайную
величину.
Пусть требуется проверить
гипотезу
![]() о
том, что эта случайная величина подчиняется
закону распределения
о
том, что эта случайная величина подчиняется
закону распределения ![]() .
Для проверки гипотезы произведём
выборку, состоящую из n независимых
наблюдений над случайной величиной X.
По выборке можно построить эмпирическое
распределение
.
Для проверки гипотезы произведём
выборку, состоящую из n независимых
наблюдений над случайной величиной X.
По выборке можно построить эмпирическое
распределение ![]() исследуемой
случайной величины. Сравнение эмпирического
распределения
и
теоретического (или, точнее было бы
сказать, гипотетического — то есть
соответствующего гипотезе
)
распределения
производится
с помощью специального правила — критерия
согласия.
Одним из таких критериев и является
критерий Пирсона.
исследуемой
случайной величины. Сравнение эмпирического
распределения
и
теоретического (или, точнее было бы
сказать, гипотетического — то есть
соответствующего гипотезе
)
распределения
производится
с помощью специального правила — критерия
согласия.
Одним из таких критериев и является
критерий Пирсона.
Для проверки критерия вводится статистика:
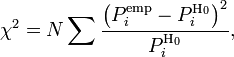
где ![]() —
предполагаемая вероятность попадания
в
—
предполагаемая вероятность попадания
в ![]() -й
интервал,
-й
интервал, ![]() —
соответствующее эмпирическое значение,
—
соответствующее эмпирическое значение, ![]() —
число элементов выборки из
-го
интервала,
—
число элементов выборки из
-го
интервала, ![]() —
полный объём выборки. Также используется
расчет критерия по частоте, тогда:
—
полный объём выборки. Также используется
расчет критерия по частоте, тогда:
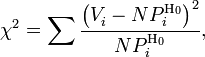
где ![]() —
частота попадания значений в интервал.
Эта величина, в свою очередь,
является случайной (в
силу случайности
)
и должна подчиняться распределению
—
частота попадания значений в интервал.
Эта величина, в свою очередь,
является случайной (в
силу случайности
)
и должна подчиняться распределению
![]() .
.
Проверка статистических гипотез осуществляется с помощью статистического критерия (назовем его в общем виде К), являющегося функцией от результатов наблюдения.
Статистический критерий – это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н0.
Как уже отмечалось выше, следует иметь в виду, что статистическая проверка гипотез имеет вероятностный характер, так как принимаемые вывод основываются на изучении свойств распределения случайной переменной по данным выборки, а потому всегда существует риск допустить ошибку. Однако с помощью статистической проверки гипотез можно определить вероятность принятия ложного решения. Если вероятность последнего невелика, то можно считать, что применяемый критерий обеспечивает малый риск ошибки.
При проведении проверки статистических гипотез в первую очередь приходится решать задачи статистической проверки гипотез о:
1) принадлежности «выделяющихся» единиц исследуемой выборочной совокупности генеральной совокупности;
2) виде распределения изучаемых признаков;
3) величине средней арифметической и доли;
4) наличии и тесноте связи между изучаемыми признаками;
5) о форме корреляционной связи.
При проверке гипотез имеется возможность совершить ошибку двоякого рода:
а) ошибка первого рода - проверяемая гипотеза (нулевая гипотеза Н0) является в действительности верной, но результаты проверки приводят к отказу от нее;
б) ошибка второго рода - проверяемая гипотеза в действительности является ошибочной, но результаты проверки приводят к принятию.
В статистике в настоящее время имеется большое число критериев для проверки практически любых гипотез. Притом основные принципы их построения и применения являются общими. Для построения статистического критерия, позволяющего проверить некоторую гипотезу, необходимо следующее:
1) сформулировать проверяемую гипотезу Н0. Наряду с проверяемой гипотезой формулируется также конкурирующая (альтернативная) гипотеза;
2) выбрать уровень значимости, контролирующий допустимую вероятность ошибки первого рода;
3) определить область допустимых значений и так называемую критическую область;
4) принять то или иное решение на основе сравнения фактического и критического значений критерия.
Проверка статистических гипотез складывается из следующих этапов:
- формулируется в виде статистической гипотезы задача исследования;
- выбирается статистическая характеристика гипотезы;
- выбираются испытуемая и альтернативная гипотезы на основе анализа возможных ошибочных решений и их последствий;
- определяются область допустимых значений, критическая область, а также критическое значение статистического критерия (t, F) по соответствующей таблице;
- вычисляется фактическое значение статистического критерия;
- проверяется испытуемая гипотеза на основе сравнения фактического и критического значений критерия, и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется.
Уровнем значимости будет называться такое малое значение вероятности попадания критерия в критическую область при условии справедливости гипотезы, что появление этого события может расцениваться как следствие существенного расхождения выдвинутой гипотезы и результатов выборки. Обычно уровень значимости принимают равным 0,05 или 0,01. Исходя из величины уровня значимости, можно определить критическую область, под которой понимается такая область значений выборочной характеристики, попадая в которую они будут свидетельствовать о том, что проверяемая гипотеза должна быть отвергнута. К критической области относятся те значения, появление которых при условии верности гипотезы было бы маловероятным.
Допустим, что рассчитанное по эмпирическим данным значение критерия попало в критическую область, тогда при условии верности проверяемой гипотезы Н0 вероятность этого события будет не больше уровня значимости. Поскольку выбирается достаточно малым, то такое событие является маловероятным и, следовательно, проверяемая гипотеза Н0 может быть отвергнута.
Если же наблюдаемое значение характеристики не принадлежит к критической области и, следовательно, находится в области допустимых значений, то проверяемая гипотеза Н0 не отвергается. Вероятность попадания критерия в область допустимых значений при справедливости проверяемой гипотезы Н0 равна 1.
Чем меньше уровень значимости, тем меньше вероятность браковать проверяемую гипотезу, когда она верна, т.е. меньше вероятность совершить ошибку первого рода. Но при этом расширяется область допустимых значений и, значит, увеличивается вероятность совершения ошибки второго рода.
Все значения рассматриваемой характеристики, не принадлежащие к критической области образуют так называемую область допустимых значений. Если наблюдаемое значение характеристики находится в области допустимых значений, то проверяемая гипотеза принимается с вероятностью.
можно было бы найти критическую точку Ккр распределения f(k), которая распределила бы область допустимых значений, в которой результаты выборочного наблюдения выглядят наиболее правдоподобными, и критическую область, в которой результаты выборочного наблюдения выглядят менее правдоподобными в отношении нулевой гипотезыВыбор критерия для проверки статистических гипотез может осуществляться на основании различных принципов. Чаще всего для этого пользуются принципом отношения правдоподобия, который позволяет построить критерий, наиболее мощный среди всех возможных критериев. Суть его сводится к выбору такого критерия К с известной функцией плотности f(k) при условии справедливости гипотезы Н0, чтобы при заданном условии значимости Н0.
рассчитать по выборочным данным наблюдаемое значение критерия Кнабл и определить, является ли оно наиболее или наименее правдоподобным в отношении нулевой гипотезы Н0.Если такой критерий К выбран, и известна плотность его распределения, то задача проверки статистической гипотезы сводится к тому, чтобы при заданном уровне значимости
Проверка каждого типа статистических гипотез осуществляется с помощью соответствующего критерия, являющегося наиболее мощным в каждом конкретном случае.
Как уже отмечалось ранее, проверка статистических гипотез применяется в разных областях для изучения массовых явлений. Изучение массовых явлений, как правило, осуществляется по неполной информации. В составе собранных данных могут встречаться единичные наблюдения, у которых отдельные значения изучаемых признаков заметно отличаются от общей тенденции изменения большинства значений. Причины таких отличий могут быть разными:
1) из-за ошибок наблюдения;
2) вследствие случайного стечения различных обстоятельств, каждый из которых в отдельности несущественный, но совокупное их влияние привело к таким резко выделяющимся от общей картины значениям признаков;
3) как следствие нарушения однородности изучаемой совокупности.
В общем случае все значения изучаемых признаков фиксируются по известным единицам совокупности по их части, отобранной с учетом всех требований. Следовательно, первичные статистические данные, включая и резко «выделяющемся», соответствуют конкретным случаям проявления изучаемого явления. Следовательно, субъективное отбрасывание «выделяющихся» единиц недопустимо.
Рассмотрим использование критериев для проверки статистических гипотез на примере закона нормального распределения. Закон нормального распределения лежит в основе многих теорем и методов статистики
- при оценке репрезентативности выборки (расчете ошибки выборки и распространении характеристик выборки на генеральную совокупность);
- измерении степени тесноты связи и составлении модели регрессии;
- построении и использование статистических критериев и др.
Как показывают многочисленные статистические исследования, частоты (частости) эмпирических распределений за редким исключением будут отличаться от значений теоретического распределения. Расхождения между частотами (частостями) эмпирического и теоретического распределения могут быть несущественными и объяснены случайностями выборки и существенными при несоответствии выбранного и эмпирического законов распределения.
Для проверки гипотезы о соответствии эмпирического распределения теоретическому закону нормального распределения используются особые статистические показатели-критерии согласия (или критерии соответствия). К ним относятся критерии К.Пирсона, А.Н. Колмогорова, Романовского, Ястремского и др.
Большинство критериев согласия базируется на использовании отклонений эмпирических частот от теоретических. Очевидно, что чем больше эти отклонения, тем хуже теоретическое распределение соответствует эмпирическому. Статистические характеристики таких критериев согласия являются некоторыми функциями этих отклонений.

 понимаемый как интеграл в смысле
Лебега. При этом функции, отличающиеся
друг от друга лишь на множество меры
нуль, считаются тождественными.
Сложение функций и умножение их на
число определяется обычным способом,
а под скалярным произведением понимается
интеграл
понимаемый как интеграл в смысле
Лебега. При этом функции, отличающиеся
друг от друга лишь на множество меры
нуль, считаются тождественными.
Сложение функций и умножение их на
число определяется обычным способом,
а под скалярным произведением понимается
интеграл
 Норма в этом случае равна
Норма в этом случае равна
 Роль единичных векторов предыдущего
примера здесь могут играть любые
функции ji(x) из L2,
обладающие свойствами ортогональности
Роль единичных векторов предыдущего
примера здесь могут играть любые
функции ji(x) из L2,
обладающие свойствами ортогональности
 и нормированности
и нормированности
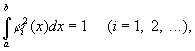 а также следующим свойством замкнутости:
если f(x) принадлежит L2 и
а также следующим свойством замкнутости:
если f(x) принадлежит L2 и
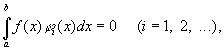 то f(x) =
0 всюду, кроме множества меры нуль. На
отрезке [0,2p]
в качестве такой системы функций можно
взять тригонометрическую систему
то f(x) =
0 всюду, кроме множества меры нуль. На
отрезке [0,2p]
в качестве такой системы функций можно
взять тригонометрическую систему
 Разложению (1) соответствует разложение
функции f(x) из L2 в
ряд Фурье
Разложению (1) соответствует разложение
функции f(x) из L2 в
ряд Фурье