Закон постоянства объема

При обработке давлением, а в частности при прокатке, происходит уменьшение высоты, увеличение ширины и длины. Объем же металла не изменяется. Это явление называют законом постоянства объема.

Математическое выражение этого закона имеет вид: ,

где - объем металла до деформации;

- объем металла после деформации;

Уравнение постоянства и объема широко применяется для расчета размеров тела при всех видах обработки металлов давлением. Зная начальные размеры тела, нетрудно определить конечные размеры и наоборот.

Если тело до деформации имело прямоугольное сечение (заготовка, полоса, лист), то исходя из закона постоянства объема, выражение будет иметь вид:

,

где - размеры тела до деформации;

- размеры тела после деформации;

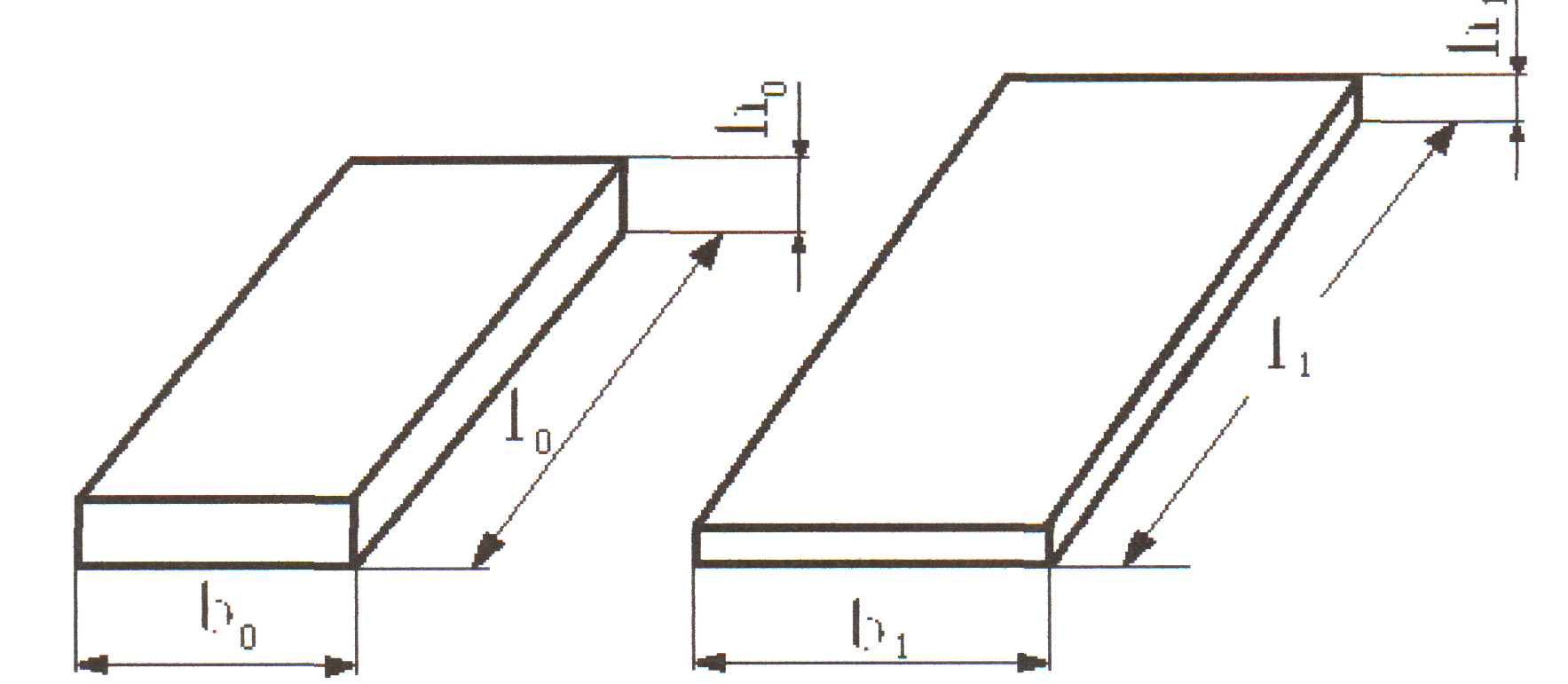
Рисунок 28 – Формоизменение заготовки прямоугольного сечения при прокатке.

Для металла круглого сечения (трубная заготовка, пруток, проволока) уравнение постоянства объема будет иметь вид:

,

где - объем металла до прокатки;

- объем металла после прокатки;

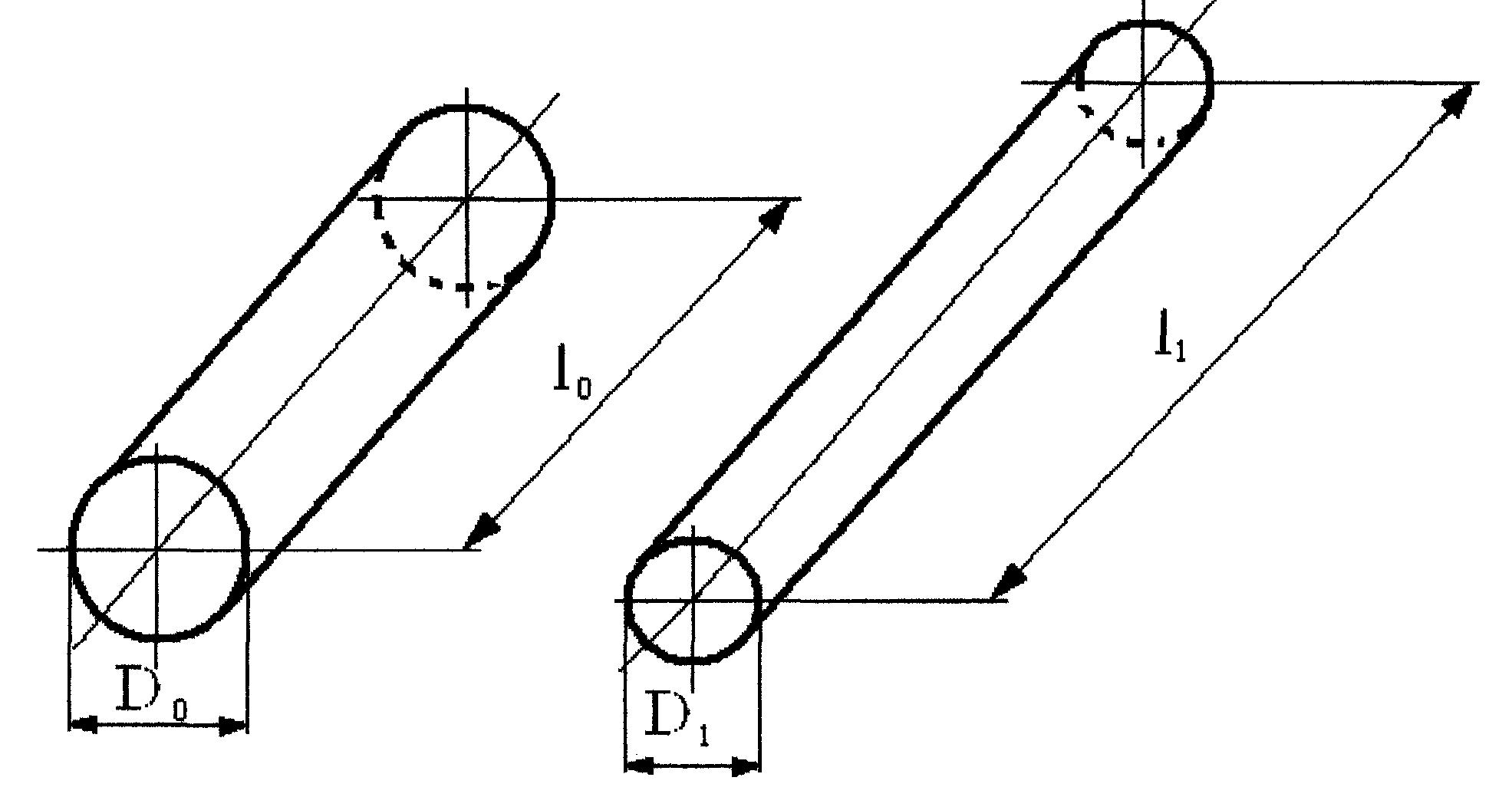
Рисунок 29 – Процесс формоизменения заготовки круглого сечения при прокатке.

При изменении геометрической формы тела в процессе обработки давлением размеры металла определяются соответственно его форме. Например, при прокатке круглой стали из блюма прямоугольного сечения, получим уравнение постоянства объема в следующем виде:

При прокатке двутавровой балки из блюма уравнение постоянства объема будет иметь вид:

При прокатке швеллера из блюма уравнение постоянства объема будет иметь вид:

При прокатке равнополочной угловой стали из блюма уравнение постоянства объема будет иметь вид:

Положение о постоянстве объема имеет отступление в двух случаях:

1. При горячей прокатке литого металла;

2. При холодной прокатке;

В первом случае объем металла после деформации несколько уменьшится. Уменьшение объема литого металла объясняется уничтожением в нем в процессе деформации различного рода неплотностей в виде газовых пузырей, рыхлостей, трещин.

Во втором случае объем металла после деформации увеличивается на 0,25%. Увеличение объема обуславливается явлением наклепа при наличии которого плотность металла несколько уменьшается.

Вывод:

Эти отступления от закона постоянства объема настолько незначительны, что при расчетах ими пренебрегают и считают, что .

Закон наименьшего сопротивления

«В случае возможного перемещения точек деформируемого тела в различных направлениях, каждая точка деформируемого тела перемещается в направлении наименьшего сопротивления» - такова формулировка закона наименьшего сопротивления, данная С.И Губкиным.

При деформации каждая точка деформируемого тела будет перемещаться в том направлении, в котором возникают наименьшие сопротивления ее перемещению. В этом заключается сущность закона наименьшего сопротивления.

Согласно этого закона при одинаковых внешних условиях, т.е. при свободном формоизменении, частицы тела будут перемещаться кротчайшими по кротчайшим путям, так как при таком перемещении они будут испытывать наименьшее сопротивление.

Известно, что кротчайшим путем является перпендикуляр, проходящий через точку к периметру сечения.

Рассмотрим проявление закона наименьшего сопротивления при осаживании нескольких образцов различного поперечного сечения: