2.1 Задания для самостоятельного решения.

Ниже приводятся результаты измерений некоторой физической величины, которые будут рассматриваться как n реализаций случайной величины X. Предполагая, что СВ Х имеет нормальное распределение, требуется:

1. Найти точечные несмещенные оценки математического ожидания а и среднего квадратического отклонения .

2. Записать плотность вероятности и функцию распределения СВ Х.

3. Найти доверительный интервал, накрывающий математическое ожидание СВ Х с заданной доверительной вероятностью Р = 1- = 0,95, считая  неизвестным.

4. Найти доверительный интервал, накрывающий среднее квадратическое отклонение  с заданной вероятностью Р = 1- = 0,95.

5. Принимая Р = 1- = 0,99, найти предельную погрешность, с которой среднее арифметическое оценивает неизвестное математическое ожидание СВ Х.

6. Найти минимальное число измерений, которое нужно произвести, чтобы с доверительной вероятностью Р = 1- = 0,95 можно было бы утверждать, что, принимая М (Х) = , мы совершаем погрешность, не превышающую  = 0,2S.

7. Вычислить:

.

2.3 Задачи для самостоятельного решения

Задача 1.

СВ Х – сопротивление резистора в кило омах.

i – номер резистора	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
xi – сопротивление резистора (ком)	4,8	6,2	6,0	5,9	5,6	4,9	6,0	6,1	5,5	5,8	5,7	5,1	5,5	6,2	5,4

Р (Х < 5) = ?

Задача 2.

СВ Х – еженедельные затраты времени ( в часах) на посещение библиотеки, определяемые путем анкетирования:

i – номер анкеты	1	2	3	4	5	6	7	8	9	10	11	12
xi – затраты времени (ч)	2,2	4,5	3,8	5,0	3,0	6,0	12,0	8,0	16,2	15,0	2,0	1,0

Р (8 < X < 14) = ?

Задача 3.

СВ Х – индуктивность катушки в мгн.

i – номер катушки	1	2	3	4	5	6	7	8	9	10
xi – индуктивность (мгн)	8,345	8,346	8,348	8,342	8,343	8,345	8,343	8,347	8,344	8,347

Р (8,345 < X < 8,349) = ?

Критерий согласия ²

Предположим, что по виду гистограммы или полигона частостей или из каких - либо других соображений удается выдвинуть гипотезу о множестве функций определенного вида (нормальных, показательных, биномиальных и т. п.), к которому может принадлежать функция распределения исследуемой СВ Х. Критерий ² Пирсона позволяет производить проверку согласия эмпирической функции распределения F*(x) с гипотетической функцией распределения F(x).

Для этого придерживаются следующей последовательности действий:

1. на основании гипотетической функции F(x) вычисляют вероятность попадания СВ Х в частичные интервалы :

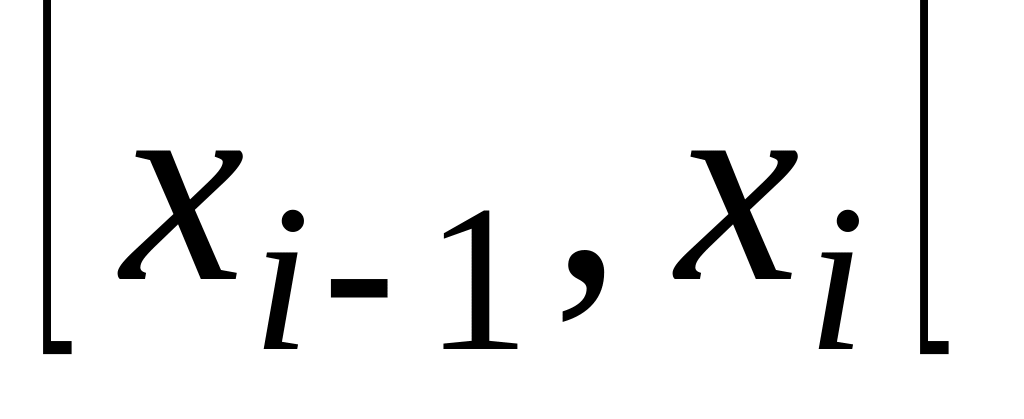; i =1, 2, ..., k;

2) умножая полученные вероятности p_i на объем выборки n, получают теоретические частоты np_i частичных интервалов ,т.е. частоты, которые следует ожидать, если гипотеза справедлива;

3) вычисляют выборочную статистику (критерий) ²:

²_набл. = .

Можно показать, что если гипотеза верна, то при распределение выборочной статистики, независимо от вида функции F(x), стремится к распределению ² с  = k-r-1 степенями свободы ( k – число частичных интервалов, r - число параметров гипотетической функции F(x), оцениваемых по данным выборки).

Критерий ² сконструирован таким образом, что чем ближе к нулю наблюдаемое значение критерия ², тем вероятнее, что гипотеза справедлива. Поэтому для проведения гипотезы применяется критерий ² с правосторонней критической областью. Необходимо найти по таблицам квантилей ² – распределения по заданному уровню значимости  и числу степеней свободы  = k-r-1 критическое значение , удовлетворяющее условию .

Если ²_набл. ²_,, то считается, что гипотетическая функция F(x) не согласуется с результатами эксперимента. Если ²_набл. ²_,, то считается, что гипотетическая функция F(x) согласуется с результатами эксперимента.

Замечание. При применении критерия ² необходимо, чтобы в каждом частичном интервале было не менее 5 элементов. Если число элементов (частота) меньше 5,то рекомендуется объединять такие частичные интервалы с соседними.

2.5 Домашняя работа.

Каждому студенту в соответствии со своим номером варианта требуется:

1. записать исходную выборку в виде таблицы;

2. построить статистический ряд;

3. записать сгруппированную выборку в виде таблицы;

4. построить график эмпирической функции распределения;

5. построить гистограмму;

6. проверить гипотезу о нормальном законе распределения случайной величины Х и записать вычисления в таблицу;

7. построить график плотности случайной величины Х.

При выполнении работы принять уровень значимости  = 0,05, отрезок [24,5; 54,5], число интервалов k = 10. Варианты индивидуальных заданий приведены в таблице.

i – му варианту соответствуют элементы выборки, расположенные в 15 – ти следующих строчках таблицы, начиная с i – й (объем выборки при этом n = 150).

1	48	39	43	44	34	34	32	43	40	46
2	25	31	34	49	39	37	45	49	31	49
3	43	46	34	35	42	32	41	34	42	42
4	38	40	46	47	34	42	38	40	38	36
5	30	43	41	40	40	35	35	41	38	45
6	37	42	38	36	44	39	32	48	43	39
7	43	30	32	36	42	34	49	48	49	50
8	37	30	44	48	44	35	45	34	33	41
9	43	45	50	34	33	39	41	39	46	31
10	40	52	44	39	35	45	33	42	42	36
11	44	51	45	39	34	44	40	37	43	32
12	33	42	40	35	37	43	48	48	50	32
13	40	48	45	43	36	36	42	40	37	30
14	44	50	46	39	41	48	44	42	36	51
15	44	50	47	37	33	34	42	43	43	47
16	33	48	38	42	45	32	34	44	39	45
17	48	26	31	34	38	36	46	49	40	48
18	42	47	35	34	41	33	41	35	43	42
19	39	37	47	47	33	42	37	39	39	37
20	43	41	30	39	38	36	36	34	42	46
21	39	44	37	35	43	38	33	47	45	38
22	37	48	38	52	40	45	44	42	38	40
23	44	46	37	34	41	37	41	39	30	38
24	32	41	48	36	51	36	33	39	45	40
25	34	41	38	34	33	27	51	45	27	38
26	42	37	46	41	47	36	30	45	41	40
27	37	37	39	42	48	41	36	39	33	47
28	43	49	27	31	41	46	40	36	36	42
29	41	46	33	37	47	35	31	29	30	36
30	48	38	37	34	40	34	36	50	48	39
31	30	38	43	41	44	45	38	37	46	50
32	41	48	41	43	47	37	42	34	32	44
33	37	48	46	41	41	37	37	48	49	46
34	38	44	50	37	47	27	48	37	46	38
35	48	47	38	52	34	36	34	41	41	32
36	31	43	34	46	37	40	41	39	32	42
37	47	33	51	41	40	45	37	36	27	36
38	37	42	46	35	34	38	45	36	20	40
39	34	48	30	51	33	41	44	42	39	39
40	45	45	41	40	36	27	50	44	41	48
41	36	36	32	32	36	49	27	45	30	35
42	40	38	45	40	40	50	42	37	50	39
43	43	38	30	59	42	41	33	42	38	44
44	44	41	47	52	51	38	50	39	50	48
45	49	43	52	50	30	30	26	50	27	49
46	27	49	46	39	47	26	49	52	29	44
47	51	53	48	49	53	45	27	43	48	44