Задачи для самостоятельного решения:
Найти закон свободных колебаний струны, закрепленной на концах и
,
если в начальный момент времени форма
струны имеет вид ломаной OAB,
где O(0;
0), A(2;
-0,1), B(3;
0). Найти форму струны в момент времени
t,
если начальные скорости точек равны
нулю.
Ответ:
.
Найти закон свободных колебаний (в случае
)
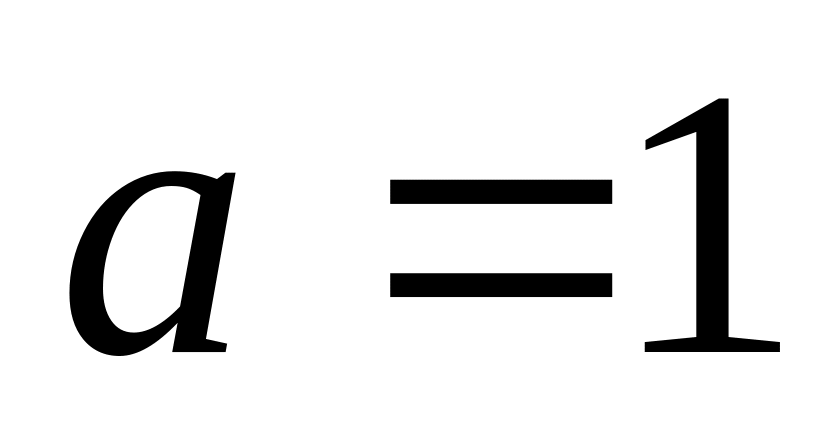струны длины 1, расположенной на отрезке
,
если в начальный момент времени струне
придали форму параболы
,
а затем струну отпустили с начальной скоростью, равной нулю.
Ответ:
.
В полуполосе
,
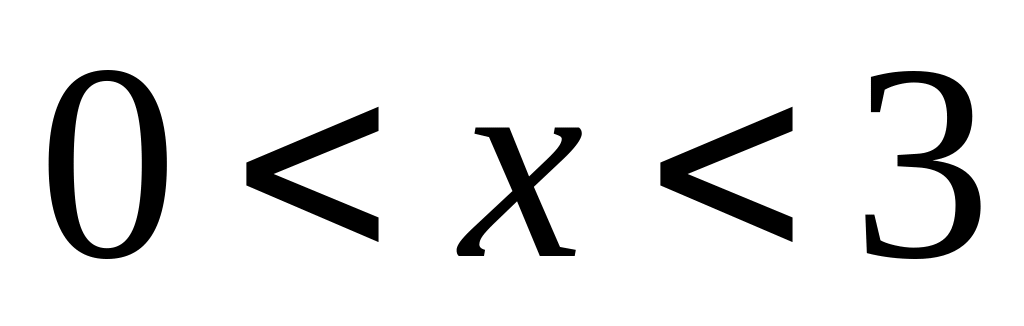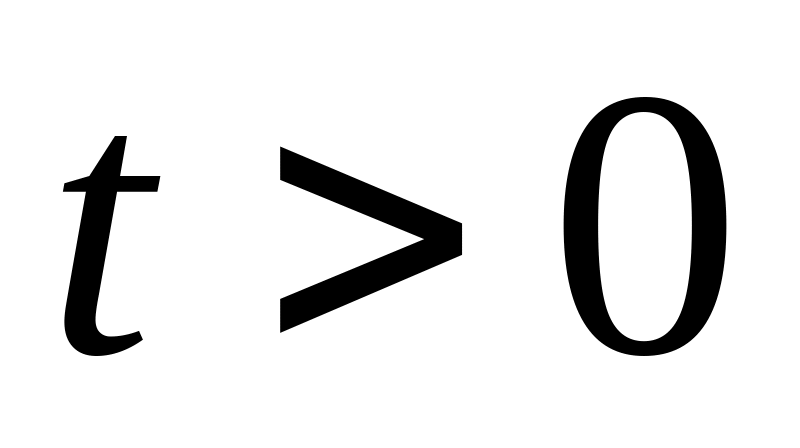для уравнения
решить смешанную задачу:
,
.
Ответ:
.
Найти закон распределения температуры
внутри стержня, у которого левый конец
(при
)
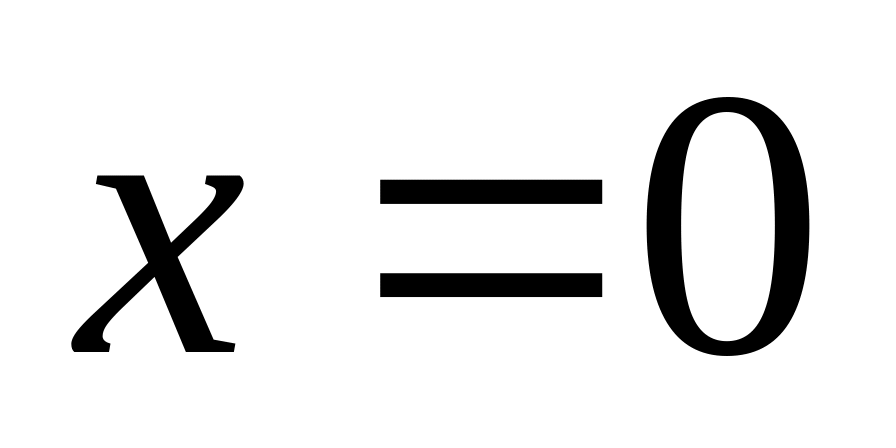поддерживают при постоянной нулевой
температуре, а правый конец (при
)
теплоизолирован от окружающей среды,
т.е.
.
Причем начальная температура стержня
задана функцией
.
Ответ:
.
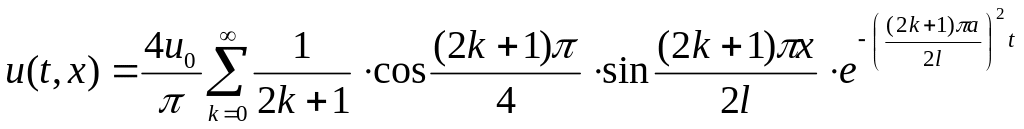Найти решение смешанной задачи
Ответ:
.
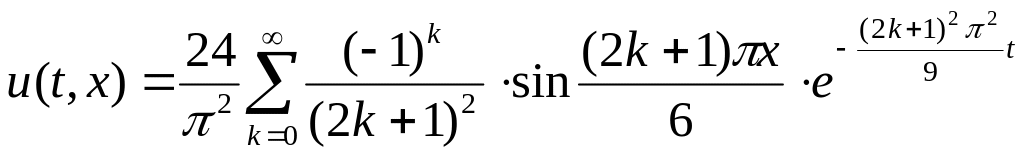Найти закон распределения температуры в стержне длиной π с теплоизолированной боковой поверхностью, если на концах стержня
и
поддерживается нулевая температура,
а начальная температура стержня задана
функцией
.
Ответ:
.