Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ряды Фурье и ДУЧП.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

2.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Задачи для самостоятельного решения Найти канонический вид уравнений:

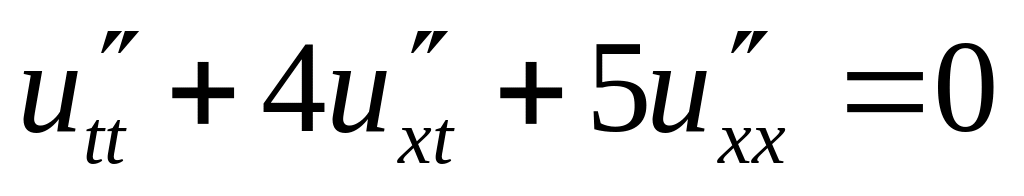Ответ: .

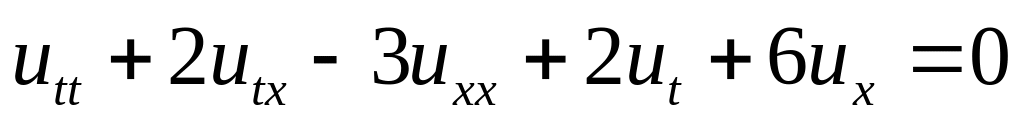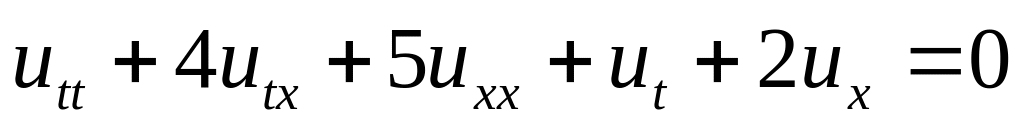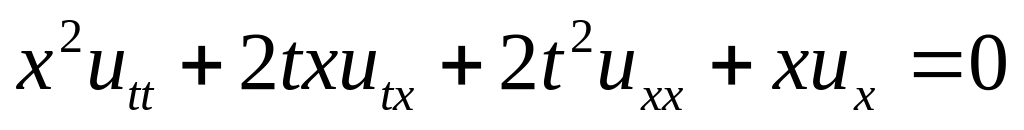Ответ: или .

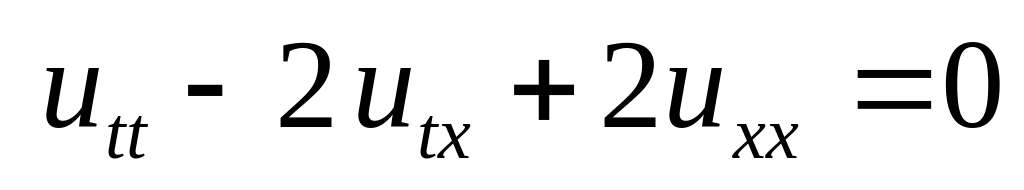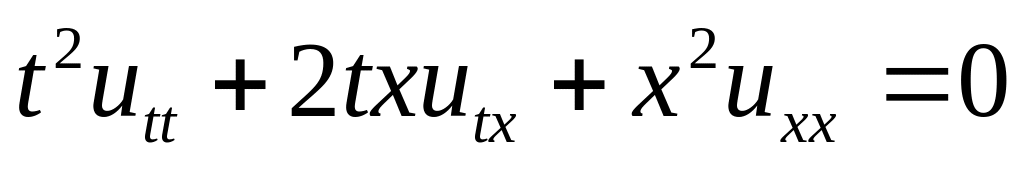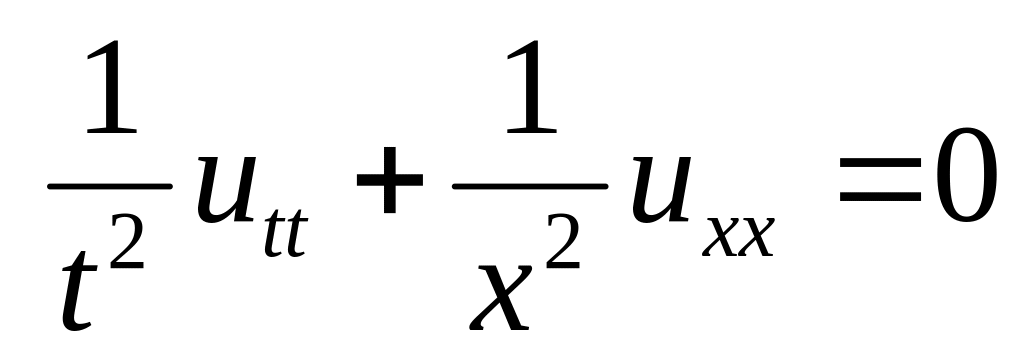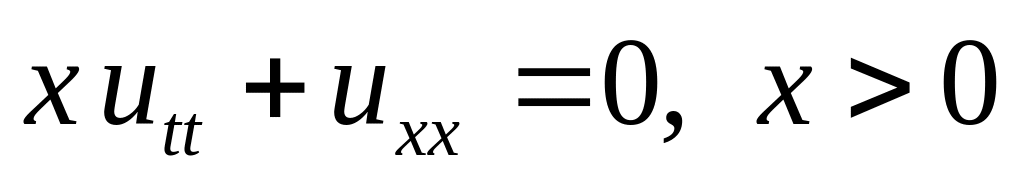Ответ: .

Задача Штурма−Лиувилля, свойства ее решений

Задача Штурма−Лиувилля, или задача о собственных значениях, возникает при решении уравнений в частных производных методом Фурье (этот метод будет рассмотрен ниже).

Рассмотрим однородное линейное дифференциальное уравнение II порядка в виде , где , λ – параметр; – непрерывно дифференцируемая на функция, а – непрерывная на функция.

Будем рассматривать краевые условия следующих типов:

а)	(I типа);
б)	(II типа);
в)	(III, смешанного типа).
г)	(III, смешанного типа).

Поставим задачу поиска таких значений параметра λ, при которых существуют ненулевые решения дифференциального уравнения , удовлетворяющие краевым условиям одного из 4-х типов. Значения λ, при которых существуют ненулевые решения, называются собственными значениями, а соответствующие им решения – собственными функциями. Задача нахождения собственных значений и собственных функций называется задачей Штурма−Лиувилля. В зависимости от типа краевых условий задачи Штурма-Лиувилля делятся на три вида:

А) I краевая задача – задача нахождения собственных функций, удовлетворяющих краевым условиям первого типа;

Б) II краевая задача – задача нахождения собственных функций, удовлетворяющих краевым условиям второго типа;

В) III краевая задача – задача нахождения собственных функций, удовлетворяющих краевым условиям третьего (смешанного) типа.

Отметим основные свойства собственных значений и собственных функций.

Основные свойства

1. Существует счетное множество значений параметра ( ) которым соответствуют собственные функции.

2. Собственные функции на , соответствующие различным значениям , ортогональны, т.е. при .

3. Всякая функция , удовлетворяющая краевым условиям одного из 4-х типов и имеющая непрерывные вторые производные, раскладывается в абсолютно сходящийся ряд по собственным функциям , т.е. , где .

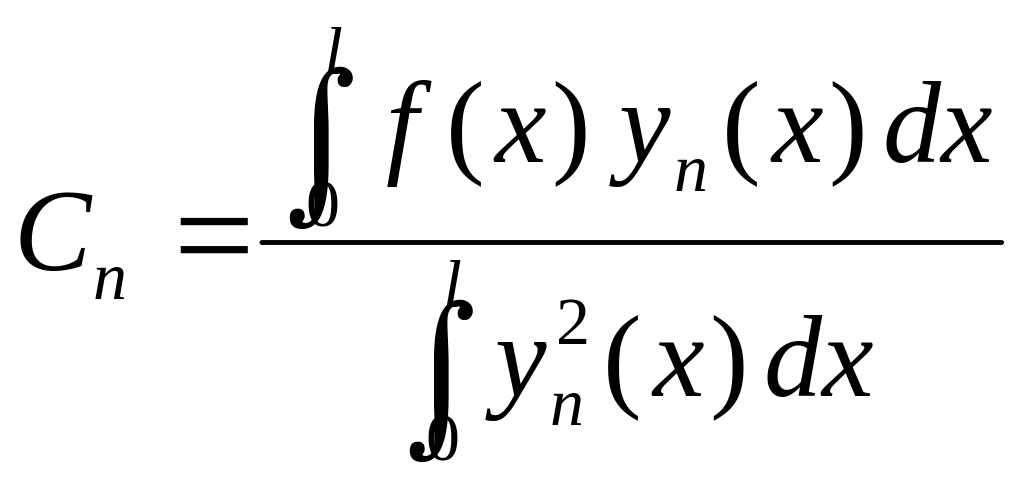Решение задачи Штурма−Лиувилля

Рассмотрим частный случай задачи Штурма−Лиувилля при , т.е. будем решать дифференциальное уравнение вида

, (4.1)

где , а . Будем решать эту задачу для наиболее типичных краевых условий.

Требуется найти функцию нетождественно равную 0, удовлетворяющую уравнению (4.1) и граничным условиям а), б), в), г). Будем искать решение в виде . Подставляя эту функцию вместе с производными в уравнение (4.1), получаем характеристическое уравнение . Тогда общее решение примет вид: , где − произвольные постоянные, .

Рассмотрим, например, II краевую задачу (б): . Из общего решения следует ; тогда

Полученные равенства представляют собой систему линейных уравнений относительно :

Подставим , полученное из первого уравнения, во второе уравнение: . Чтобы последнее уравнение имело ненулевое решение, необходимо и достаточно, чтобы . По формуле Эйлера имеем: ℤ. А следовательно , откуда . То есть , или . Полученные числа называются собственными значениями: (можем считать, что ).

Найдем собственные функции . Т.к. , то . По формуле Эйлера , поэтому . Поскольку собственные функции определяются с точностью до постоянной, то можно считать , а значит, собственные функции имеют вид: , .

По свойствам собственных функций для любой дважды дифференцируемой непрерывной функции имеем , где коэффициенты представляют собой коэффициенты разложения в ряд Фурье по косинусам.

В случае I краевой задачи (а) : собственные значения примут вид , ; а собственные функции . Аналогично разобранному случаю, для любой дважды дифференцируемой непрерывной функции имеем , где − коэффициенты разложения в ряд Фурье по синусам.