Задачи для самостоятельного решения: Разложить в ряд Фурье функции:
Ответ:
.
Ответ:
.
на
.
Ответ:
.
на
.
Ответ:
.
на
.
Ответ:
.
на
.
Ответ:
.
Ответ:
.
Ответ:
.
Ответ:
.
Ответ:
.
на
.
Ответ:
.
на
.
Ответ:
.
Ряды Фурье для четных и нечетных функций
Пусть − некоторая функция, определенная на , удовлетворяющая условиям теоремы Дирихле, тогда на указанном промежутке справедливо равенство
,
где − коэффициенты Фурье функции .
Рассмотрим частный случай разложения в ряд Фурье четных и нечетных функций.
Определение.
Функция
,
заданная на
,
называется: а) четной, если
;
б) нечетной, если
,
где
- область определения функции
.
Лемма
1. а) Пусть
функция
,
определенная на
,
− четна, тогда
.
б)
Пусть функция
,
определенная на
,
− нечетна, тогда
.
Теорема.
а) Пусть
− четная периодическая функция (
),
определенная на
,
тогда
,
т.е. ряд Фурье четной функции содержит
только слагаемые с косинусами;
б)
Пусть
− нечетная периодическая функция (
),
определенная на
,
тогда
,
т.е. ряд Фурье четной функции содержит
только слагаемые с синусами.
Пусть
функция
задана на
.
Дополним эту функцию произвольным
образом на
так, чтобы полученная функция удовлетворяла
тем же условиям, что и
.
Дополненную функцию можно разложить в
ряд Фурье с периодом
.
Рассмотрим два частных случая.
а)
Пусть
дополнена на
«четным» образом, т.е. для всех
:
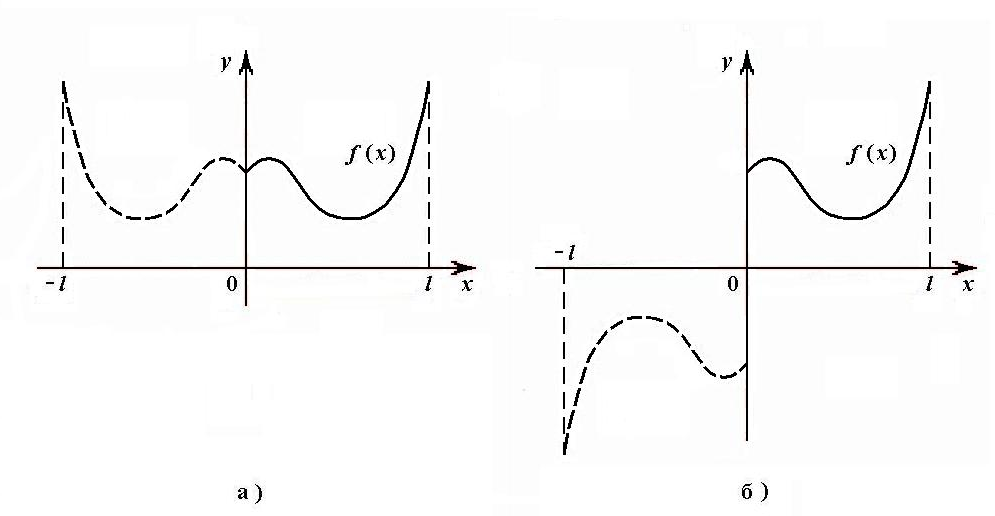
Рис. 5.
Тогда
на
получим четную функцию (рис. 5а), причем
,
.
Эту функцию можно разложить в ряд Фурье
по косинусам.
б)
Если же
дополнена на
«нечетным» образом, т.е. для всех
,
причем
,
,
тогда получаем на
нечетную функцию, которую можно разложить
в ряд по синусам (рис. 5б).
Итак, всякую непериодическую функцию, заданную на и удовлетворяющую определенным условиям, можно разложить в ряд Фурье тремя способами: (1) в общий ряд Фурье, (2) только по косинусам, (3) только по синусам. Первый случай был разобран в предыдущей теме.
В случае четного продолжения (сл.(2)) разложение в ряд Фурье примет вид:
~
, (2.1)
где
(2.2).
В случае нечетного продолжения (сл.(3)) разложение в ряд Фурье примет вид:
~
, (2.3)
где
(2.4).
Пример
1.
Найти ряд Фурье 2π
− периодической функции
,
которая задается на отрезке
равенством
.
Решение. График функции изображен на рисунке 6:
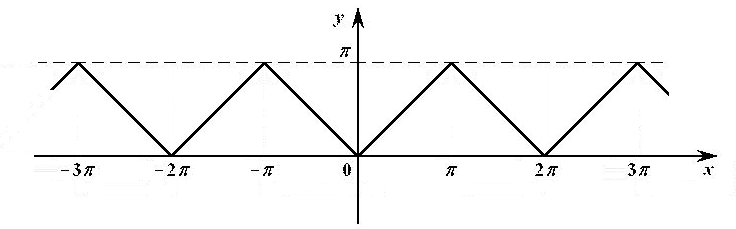
Рис. 6.
Эта
функция непрерывна в любой точке
ℝ
и кусочно-непрерывно дифференцируема,
т.к.
имеет в точках
ℤ)
разрыв первого рода, а в остальных точках
− непрерывна. Следовательно, условия
теоремы Дирихле выполнены при
,
и рассматриваемую функцию можно разложить
в ряд Фурье (1.1), сходящийся в любой точке
ℝ
к
.
Учитывая четность функции , ее коэффициенты вычисляем по формулам (2.2):
;
По формуле (2.1) находим:
ℝ.
Ответ:
при
ℝ.
Пример
2.
Функцию
,
заданную на интервале
,
разложить в ряд Фурье по синусам.
Решение.
Рассмотрим
вспомогательную функцию
,
график которой изображен на рисунке 7.
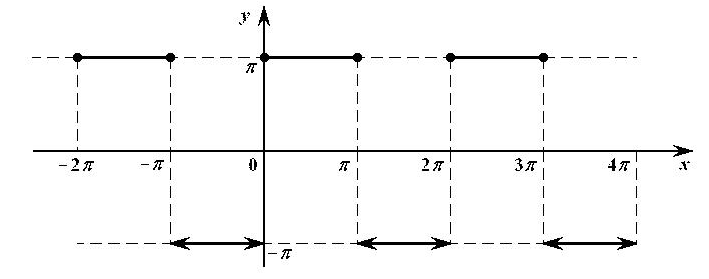
Рис. 7.
Эта функция 2π-периодическая, нечетная. По формулам (2.4) вычисляем:
,
где
ℕ.
Следовательно, согласно теореме Дирихле получаем по формуле (2.3):
.
Ответ: .
Пример
3.
Разложить в ряд Фурье функцию
,
где
.
Решение. Рассмотрим 2π − периодическую функцию , определенную на ℝ и совпадающую с на интервале (рисунок 8).
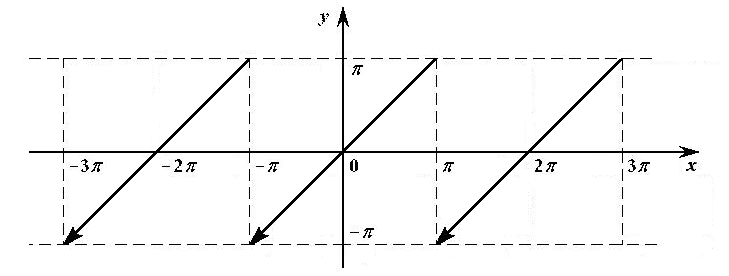
Рис. 8.
Функция
является 2π
– периодической, кусочно-непрерывной
и кусочно-непрерывно дифференцируемой.
Причем функции
и
терпят разрывы первого рода в точках
вида
ℤ.
Следовательно, ряд Фурье, составленный
для функции
,
совпадает при
с функцией
.
Поэтому учитывая нечетность функции
и формулы (2.4) при
,
получаем:
.
Значит, по формуле (2.3) находим искомое разложение:
.
Ответ:
Пример
4.
Функцию
,
заданную на отрезке
,
разложить в ряд Фурье по косинусам.
Решение. Рассмотрим Т−периодическую (Т=4) четную функцию , график которой изображен на рисунке 9.
Рис. 9.
Для этой функции по формулам (2.2) находим коэффициенты ряда Фурье:
;
где
ℕ.
Следовательно, согласно теореме Дирихле получаем по формуле (2.1):
.
Ответ: .
Пример
5.
Разложить в ряд Фурье функцию
а) на интервале по синусам;
б) на по косинусам;
в) на .
Решение. а) Чтобы разложить функцию на интервале только по синусам, рассмотрим ее нечетное 2π−периодическое продолжение на всю числовую ось (рисунок 10).
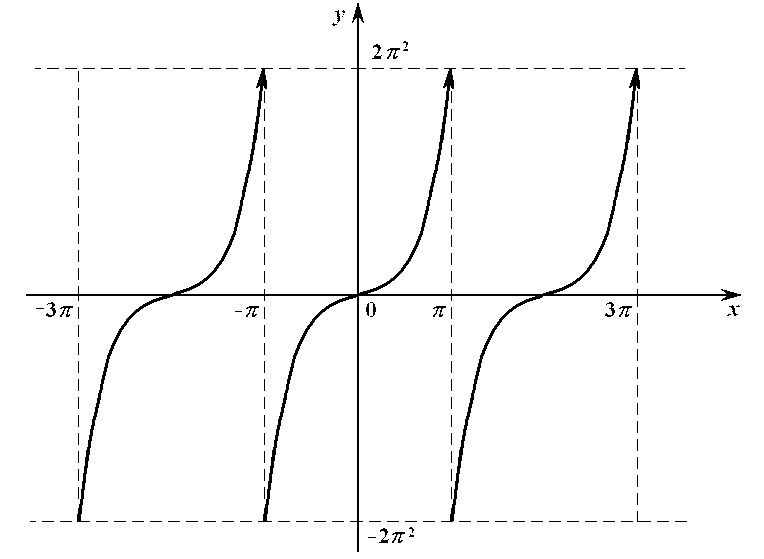
Рис. 10.
Найдем для этой функции коэффициенты Фурье:
где
ℕ.
Следовательно,
для всех
справедливо равенство:
.
б) Чтобы разложить функцию на только по косинусам, рассмотрим ее четное 2π−периодическое продолжение на всю числовую ось (рисунок 11).
Рис. 11.
Найдем для этой функции коэффициенты Фурье:
,
,
ℕ.
Следовательно, при для функции справедливо равенство:
.
в) Для того чтобы функцию разложить на интервале , рассмотрим ее 2π−периодическое продолжение на всю числовую ось, что графически представлено на рисунке 12.
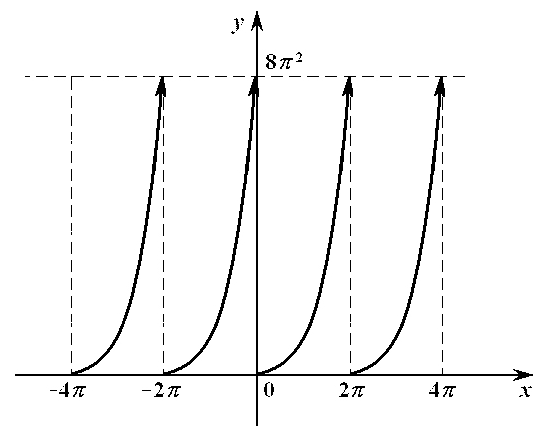
Рис. 12.
Для этой функции вычислим коэффициенты Фурье:
,
,
ℕ.
,
ℕ.
Следовательно, на для функции справедливо представление:
.
Ответ:
а)
;
б)
;
в)
.
Пример
6.
Пользуясь разложением функции в ряд
Фурье на отрезке
,
найти сумму ряда:
а)
,
б)
.
Решение.
Функция
,
заданная на отрезке
и продолженная четным образом, имеет
ряд Фурье:
. (2.5)
Следовательно, при из выражения (2.5) находим:
.
При
формула (2.5) принимает вид:
. Ответ:
а)
,
б)
.
Задачи для самостоятельного решения
Разложить в ряд Фурье функции:
а)
по косинусам, б) по синусам.
Ответ:
а)
.
б)
.
по
косинусам.
Ответ:
.
на
по синусам.
Ответ:
.
по
косинусам.
Ответ:
.
на
по синусам.
Ответ:
.
на
по синусам.
Ответ:
.
Линейные уравнения в частных производных II порядка,
свойства решений, приведение к каноническому виду
Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость - производная от расстояния; аналогично, ускорение - производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
В
этом разделе рассмотрим лишь частный
случай дифференциальных уравнений,
содержащих неизвестную функцию, зависящую
от нескольких переменных, а именно
линейное
дифференциальное уравнение в частных
производных (ЛДУрЧП)
II
порядка для функции 2-х переменных
,
которое имеет вид:
. (3.1).
Коэффициенты
уравнения
могут быть функциями только от x,
y
или постоянными, в последнем случае
имеем ЛДУрЧП с постоянными коэффициентами,
причем
.
Выражение
называют главной
частью уравнения
(3.1), а линейную часть обычно обозначают
.
Рассмотрим лишь случай действительно-значных
коэффициентов.
Если
,
то уравнение (3.1) является однородным,
если
− неоднородным.
В случае
линейное дифференциальное уравнение
(3.1) приобретает вид:
(3.2).