Ряды Фурье для периодических и непериодических функций

Пусть функция определена на ℝ.

Определение. Функция называется периодической на ℝ, если существует такое , что ℝ . Наименьшее из таких чисел Т называют периодом функции.

Основные свойства.

1. Если Т – период , то числа 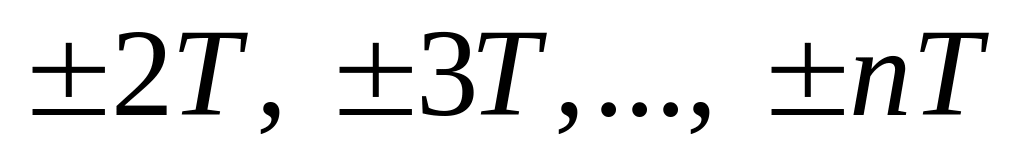− также являются периодами.

2. Сумма, разность, произведение, частное функций периода Т суть также периодические функции.

3. Если функция является периодической с периодом Т, и она интегрируема на некотором отрезке длиной Т, то интегрируема на любом отрезке длиной Т и

ℝ.

4. Если функция является нечетной на отрезке 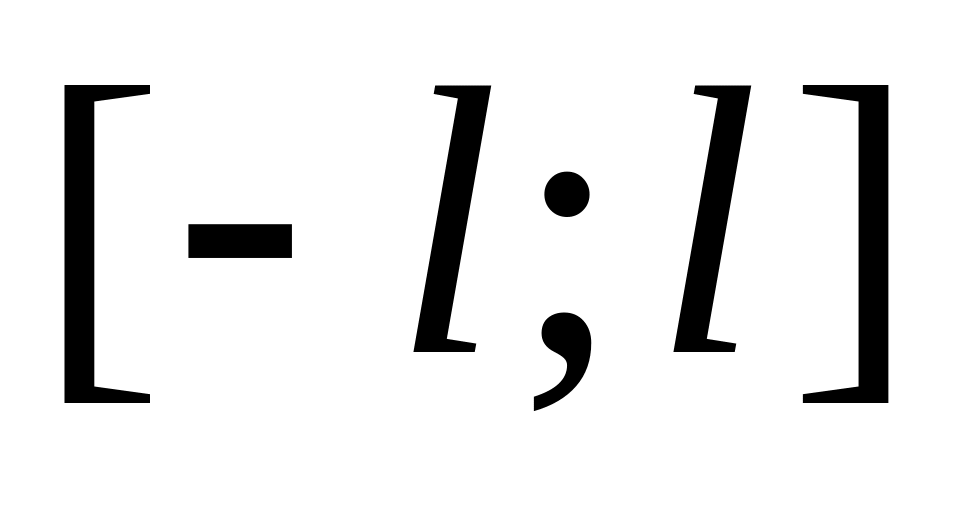с периодом 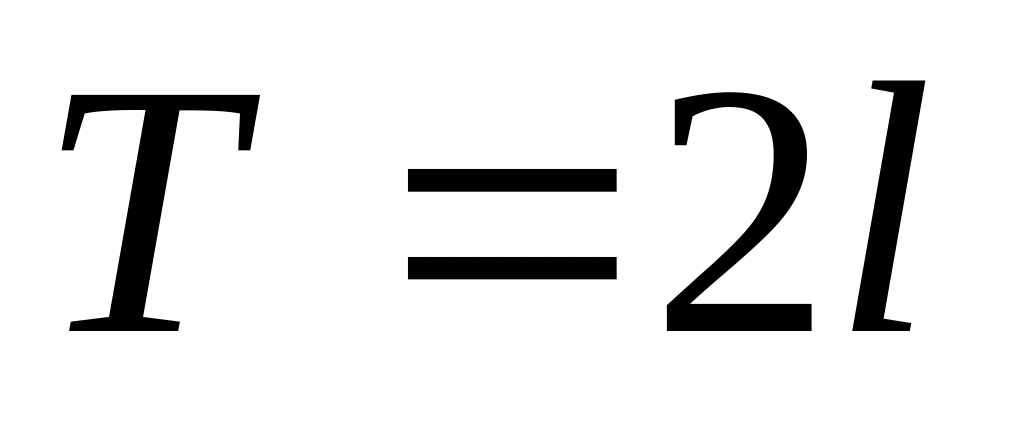, то .

5. Если функция является четной на отрезке с периодом , то .

Заметим, что всякая периодическая функция полностью определяется своими значениями на любом промежутке , где T – ее период функции. Обычно в качестве промежутка для рассмотрения выбирается симметричный промежуток , , который носит название основного периода.

Пусть на задана произвольная функция , причем значения на концах отрезка и могут не совпадать. Если продолжить ее периодически с периодом , то получим функцию:

, ℤ.

где С совпадает со значением на концах промежутка , если ; в противном случае оно выбирается произвольно. Отметим, что если даже непрерывна на , то ее продолжение может быть разрывной функцией, если .

Понятия тригонометрической системы, тригонометрического ряда

Определение 1. Основной тригонометрической системой функций называется следующая совокупность периодических функций:

.

Все эти функции имеют основной период , хотя функции и имеют меньший период .

Определение 2. Общей тригонометрической системой функций периода называется следующая система функций:

,

где . Основной период этой системы и все функции задаются на отрезке .

Определение 3. Тригонометрическим рядом называется функциональный ряд вида:

,

где − коэффициенты тригонометрического ряда.

Частичная сумма этого ряда − линейная комбинация первых функций основной тригонометрической системы и называется тригонометрическим многочленом степени n, если хотя бы одно из . Этот ряд сходится, если , причем будет также периодической функцией с периодом .

Определение 4. Общим тригонометрическим рядом называется ряд вида:

.

Если он сходится, т.е. , то его сумма является периодической функцией с периодом .

Ортогональность тригонометрической системы

Определение. Система функций , называется ортогональной на отрезке , если , а если при этом , то такая система называется ортонормированной.

Теорема. Общая тригонометрическая система функций , , ортогональна на отрезке , причем

1) , , ; 2) ; 3) , ; 4) , ; 5) ,

Ряд Фурье для функции с периодом

Пусть дана периодическая функция с периодом T. Рассмотрим основной период , . Сопоставим этой функции тригонометрический ряд

~ .

Теорема. Если функция периодична с периодом и непрерывна на , а тригонометрический ряд сходится для всех , и при этом его можно почленно интегрировать в области сходимости, то если сумма указанного ряда , т.е. , тогда коэффициенты этого ряда вычисляются по формулам (1) ; (2) ; (3) .

Определение. Тригонометрический ряд называется рядом Фурье для функции на отрезке , а коэффициенты , вычисляемые по формулам (1), (2), (3), называются коэффициентами Фурье.

Следствие теоремы. Если , то коэффициенты Фурье функции на отрезке определяются по формулам (1*) ; (2*) ; (3*) .