Графика системы MatLab
В режиме прямых вычислений доступны почти все возможности системы, в том числе построение графиков. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах.
Двумерная графика. Для построения графика необходимо выполнение следующих действий:
• задать интервал изменения аргумента;
• использовать команду построения графиков plot.
Пример:
>> x=0:0.1:10;
>> plot(sin(x))
Построение в одном окне графиков нескольких функций. Функции могут быть обозначены переменными, не имеющими явного указания аргумента: y1=sin(x); y2=cos(x); y3=x*sin(x). Это обусловлено тем, что переменные y1, y2, y3 являются векторами, как и переменная x. Используем одну из форм команды plot(a1,f1,a2,f2,a3,f3,…), где a1, a2, a3 –векторы аргументов функций (в нашем случае они все - x), а f1, f2, f3 – векторы значений функций, графики которых строятся в одном окне.
Для построения в одном окне графиков нескольких функций неоюходимо:
• задать эти функции;
• использовать одну из команд plot, например plot(a1,f1,a2,f2,a3,f3,…);
Пример (рисунок 1.3):
>> x=-5:0.5:5;
>> y1=sin(x); y2=cos(x); y3=sin(x)./х;
>> plot(x,y1,x,y2,x,y3)
Обратите внимание на задание третьей функции. Если х представляет собой массив (вектор), то нельзя использовать оператор матричного деления (/) (или умножения (*)). При вычислении функции, в нашем случае - sin(x)/x, надо использовать оператор почленного деления (./). При таком задании функции построение графика возможно, но возникает предупреждение о делении на ноль, в момент, когда х=0:
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this warning.)
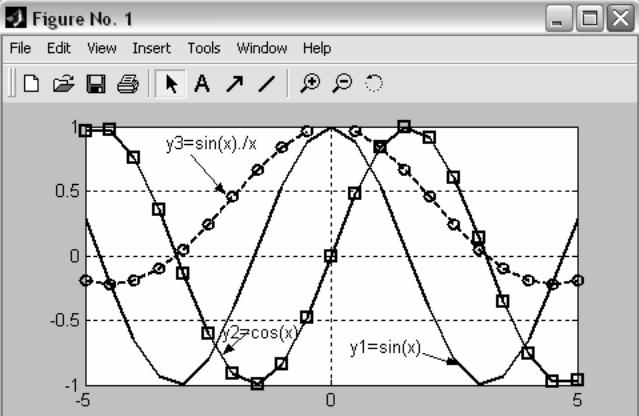
Рисунок 1.3 – График 3-х функций y1=sin(x); y2=cos(x); y3=sin(x)./х
Команда fplot. Команда fplot(‘f(x)’,[xmin xmax]) позволяет строить графики функций, которые имеют устранимые неопределенности. Команда fplot позволяет строить графики функции f(x), заданной в символьном виде, в интервале изменения аргумента x от xmin до xmax без фиксированного шага изменения x.
Пример (рисунок 1.4):
>> clear; fplot('sin(x)/x',[-15,15]); grid on
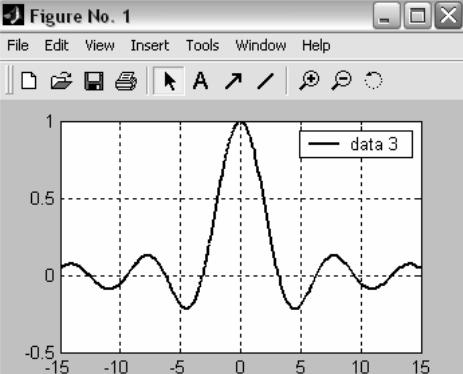
Рисунок 1.4 – График выполнения команды fplot('sin(x)/x',[-15,15]).
Здесь команда clear очищает графическое окно, а команда grid on включает отображение сетки.
Столбцовые диаграммы (команда bar(V)). В прикладных расчетах часто встречаются графики, именуемые столбцовыми диаграммами, отражающие содержание некоторого вектора V. При этом каждый элемент вектора представляется столбцом, высота которого пропорциональна значению элемента. Столбцы нумеруются и масштабируются по отношению к максимальному значению наиболее высокого столбца. Особенно часто столбцовые диаграммы используются при представлении данных финансово-экономических расчетов.
Пример (рисунок 1.5):
>> V=[1,2,3,4,5,4,3,2,1];
>> bar(V)
Рисунок 1.5 – Результат выполнения команды bar(V)
График в виде ступенчатой линии (команда stairs(x,f(x))) (рисунок 1.6).
>> x=-5:0.1:5;
>> stairs(x,x.^2)
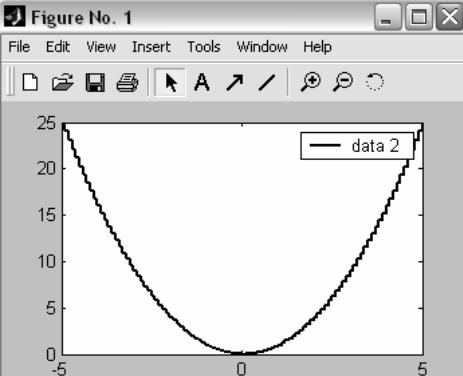
Рисунок 1.6 – Результат выполнения команды stairs(x,x.^2)
График в виде «стебельков» (команда stem(x,y)) (рисунок 1.7).
>> x=-5:0.1:5;
>> y=x.^3;
>> stem(x,y)
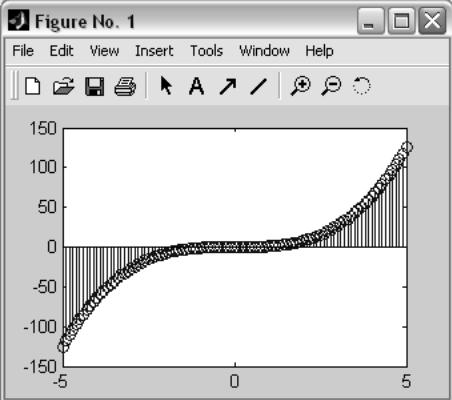
Рисунок 1.7 – Результат выполнения команды stem(x,y)
Трехмерная графика. В MATLAB имеется функция plot3(x,y,z), которая является трехмерным аналогом функции plot, т.е. она позволяет строить линию в трехмерном пространстве по координатам точек. Для построения графика функции двух переменных в виде поверхностей используют функции:
• mesh(x,y,z) – построение поверхности в виде сетки с закрашенными ребрами и незакрашенными четырехугольными ячейками;
• meshc(x,y,z) – комбинация функций mesh и contour. Линии уровня выводятся на нижней координатной плоскости;
• meshz(x,y,z) – то же что и mesh, но с краев построенной сетчатой поверхности вниз спадает «занавес»;
surf(x,y,z) – построение сетчатой поверхности. Координаты углов каждой ячейки задаются значениями четырех соседних элементов массивов x,y,z с индексами (i,j), (i, j+1), (i+1, j), (i+1, j+1). Значение массива z рассчитываются по формуле функциональной зависимости с использованием поэлементных операций над массивами x,y;
• surfc(x,y,z) - комбинация функций surf и contour. Линии уровня выводятся на нижней координатной плоскости;
• waterfall(x,y,z) – то же что и mesh, но ребра, разделяющие ячейки, проводятся только вдоль оси OX. В результате объемное тело выглядит «нарезанным на ломтики»;
• stem3(x,y,z) – вывод трехмерного графика в виде «стебельков», начинающихся при z=0 в точках, задаваемых массивами x,y. Высота «стебельков» определяется массивом z;
• contourf(x,y,z) – то же что contour, но пространство между линиями равного уровня окрашено в разные цвета в зависимости от значений z;
• contour3(x,y,z) - то же что contour, но линии равного уровня рисуются не в одной плоскости, а в зависимости от значений z;
• pcolor(x,y,z) – строит двумерный график, представляющий собой сетку. Тот же результат можно получить, если для поверхности, построенной с помощью функции surf, установить точку обзора точно сверху
Команда surf:
• сначала надо задать (сетку) диапазон изменения параметров x и y. Удобнее всего массивы формировать с помощью специальной функции [x,y]=meshgrid(x,y). Формируемые массивы имеют length(y) строк и length(x) столбцов;
• затем задать функцию, зависящую от двух переменных;
• применить функцию surf.
x=-5:0.2:5;
[x,y]=meshgrid(x);
z=sinc(sqrt(x.^2+y.^2));
surf(x,y,z)
colormap gray (вывод графика серого
цвета)
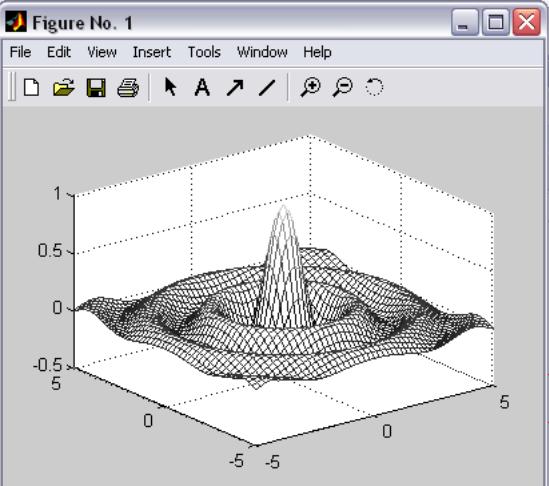
Рисунок 1.8 – Результат выполнения команды surf(x,y,z)
Команда mesh(x,y,z) (рисунок 1.9).
>>[x,y]=meshgrid(-5:0.1:5);
>> z=x.*sin(x+y);
>> mesh(x,y,z)
Рисунок 1.9 – Результат выполнения команды mesh(x,y,z)
Графики разного типа в одном окне. При необходимости можно расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды:
• subplot – создает новые объекты класса axes (подокна);
• subplot(m,n,p) - или subplot(mnp) – разбивает графическое окно на m*n подокон, где m – число подокон по горизонтали, n – по вертикали, а p – номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам);
• subplot(H), где H – дескриптор для объекта axes, дает альтернативный способ задания подокна для текущего графика;
• subplot(‘position’, [left bottom width height]) – создает подокно с заданными нормализованными координатами (в пределах от 0.0 до 1.0);
• subplot(111) и clf reset – удаляют все подокна и возвращают графическое окно в обычное состояние.
Пример. Построим четыре графика различного типа в одном окне с помощью функции subplot (рисунок 1.10):
>> x=-5:0.1:5;
>>[x,y]=meshgrid(x);
>> z=x.^2+y.^2;
>> subplot(2,2,1),plot(x,sin(x))
>> subplot(2,2,2),plot(sin(5*x),cos(2*x+0.2))
>> subplot(2,2,3), plot3(x,y,z)
>> subplot(2,2,4),surf(peaks) {где peaks – встроенный объект}
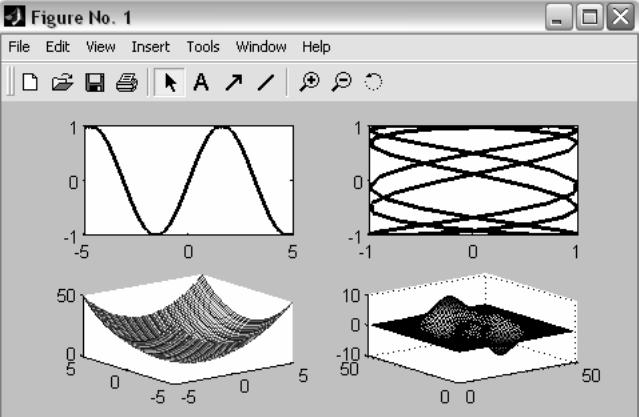
Рисунок 1.10 – Четыре графика в одном окне