9.2. Обмен и эффективность распределения ресурсов

9.2.1. Ящик Эджуорта.

Сделаем предположение, что экономика, условия общего экономического равновесия которой мы хотим изучить, не имеет производства, и состоит из двух участников (или двух агрегированных групп потребителей), А и В, каждый из которых по условию наделен комбинациями двух благ: блага X и блага Y в количестве (Х_А⁰, У_А⁰) и (Х_В⁰, У_В⁰) соответственно. Считаем, что для участников А и В выполняются аксиомы рациональности потребителя, т.е. предпочтения А и В представлены гладкими и непрерывными кривыми безразличия, имеющими убывающие нормы предельного замещения и т. д. Оба участника стараются максимизировать свою полезность.

Определим условия, при которых максимум полезности получит каждый участник.

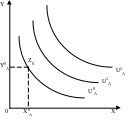
а)

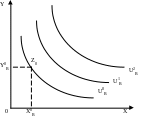
б)

Рис.9.1 Первоначальный набор благ Х и Y: а) для участника А; б) для участника В

На рис.9.1а точка Z_A представляет начальное положение участника А, имеющего Х_А⁰ единиц блага X и У_А⁰ единиц блага У. На рис.9.1б точка Z_В представляет начальное положение участника В, имеющего Х_В⁰ единиц блага X и У_В⁰ единиц блага У. Если обмен отсутствует, участник А будет иметь уровень полезности, представленный кривой безразличия U_А⁰, к которой принадлежит точка Z₀ (Х_А⁰, У_А⁰), а участник В будет иметь уровень полезности, представленный кривой безразличия U_В⁰, к которой принадлежит точка Z₀ (Х_В⁰, У_В⁰). Если участник А и участник В имеют возможность обмениваться благами, то они смогут увеличить свою полезность, перейдя на более высокую кривую безразличия. Эта возможность зависит от норм обмена благами X и У.

Из теории потребления мы знаем, что потребитель достигает своего оптимума в точке касания его бюджетной линии и кривой безразличия. Но мы исходим из предположения, что нами рассматривается модель экономики, в которой не существует денег (например, имеет место бартер). Поэтому нормы обмена благ X и У не являются их денежными ценами, несмотря на это мы будем использовать бюджетное ограничение, считая, что существуют какие то идеальные деньги как средства счета.

9.2.2. Ящик Эджуорта и кривая контрактов

Ящик (коробка) Эджуорта, назван так по имени английского экономиста Фрэнсиса Исидро Эджуорта (1845-1926), позволяет проанализировать условия простого обмена в экономике без производства при наличии двух участников, А и В, и двух благ Х иY. Эджуорт совместил карты кривых безразличия участника А и участника В повернув на 180°. семейство кривых безразличия участника В. При этом начала координат каждой из двух карт кривых безразличия становятся противолежащими вершинами прямоугольника А, В — ящика Эджуорта. (Таким образом кривые безразличия участника А выпуклы влево вниз, а кривые безразличия участника В выпуклы вправо вверх. Благо Х и благо У для участников А и В – одни и те же блага) (рис. 9.2).

На горизонтальных осях ящика Эджуорта откладывается количество блага Х, на вертикальных - количество блага Y. На нижней горизонтальной оси Х_А, от начала координат откладывается количество блага X, которое имеет участник А равное АХ_А, на верхней горизонтальной оси, Х_В, от начала координат участника В откладывается количество блага X, ВХ_В. На левой вертикальной оси, Y_A, таким же образом откладывается количество блага У, которым располагает участник А, АY_А , а на правой вертикальной оси Y_B, — количество блага У, ВY_В которым располагает участник В. Границы ящика Эджуорта соответствуют суммарным фиксированным количествам благ X и У, находящимся в распоряжении участников А и В, так что AG = ВF = Х_А + Х_В и АF = BG = Y_A + Y_B. т.к. мы сделали допущение, что в данной модели нет производства.

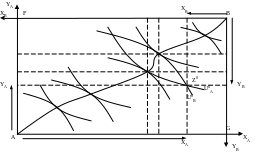
Рис.9.2.Ящик Эджуорта

В ящике Эджуорта любая точка характеризует некоторое распределение двух благ, X и У, между двумя участниками, А и В. Пусть, например, точка Z⁰ будет точкой первоначального распределения благ X и У между участниками А и В. ( рис.9.3). Участник А будет иметь набор Z⁰ (Х⁰_А,У⁰_А), участник В — набор Z⁰ (X⁰_B,Y⁰_B) и все наличное количество благ X и У будет без остатка распределено между ними:

АХ⁰_А + ВХ⁰_В = AG = ВF (9.1)

АУ⁰_А + ВУ⁰_В = АF = BG (9.2)

(Если бы первоначальное распределение благ X и У было таким, что участнику А досталось бы только благо X, а участнику В только благо У, то точкой первоначального распределения была бы правая нижняя вершина ящика Эджуорта, точка G, в которой выполняются условия: АХ⁰_А = AG = ВF , ВХ⁰_В = О; BY_B = BG = AF, AY_A =0). В точке Z⁰ наклоны пересекающихся здесь кривых безразличия А и В ( U⁰_A и U⁰_B) неодинаковы, поэтому для участников А и В первоначальное распределение благ в точке Z⁰ не является оптимальным (предельные нормы замены благ X и У в этой точке неравны). Участник А будет стремиться обменять часть имеющегося у него количества блага X на некоторое количество блага У, а участник В - обменять часть имеющегося у него количества блага У на некоторое количество блага X (рис. 9.3).

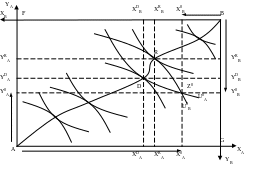
Рис 9.3. Ящик Эджуорта и контрактная кривая

Таким образом, у обоих участников существует желание улучшить свое положение в результате взаимного добровольного обмена определенными количествами благ X и У до тех пор, пока такое улучшение станет невозможным. Обмен прекратится лишь тогда, когда конечное распределение благ X и У, полученное в ходе обмена между участниками А и В, окажется в точке касания кривых безразличия обоих участников, т.е. будет достигнуто оптимальное распределение (точки D или R на рис.9.3).

Из теории потребления мы знаем, что плотность кривых безразличия велика, поскольку через любую точку на плоскости можно провести кривую, поэтому ящик Эджуорта вмещает бесконечное множество точек касания кривых безразличия двух участников. Если соединить все точки касания кривых безразличия двух участников, то получим контрактную кривую. Она соединяет все точки касания кривых безразличия участников А и В и представляет собой все множество взаимоприемлемых результатов обмена двух участников (кривая АВ на рис.9.3). Но не все взаимоприемлемые результаты обмена будут одинаково выгодны обоим участникам.

Исследуем точки D и R, лежащие на контрактной кривой АВ и являющиеся точками касания кривых безразличия участников А и В. Для того, чтобы попасть из точки первоначального распределения благ Z⁰ в точку нового распределения благ D участник В обменяет Y⁰_BY^D_B единиц блага У на Х⁰_АХ^D_А единиц блага X и окажется на более высокой кривой безразличия U¹_В, т.е. улучшит свое положение. Участник А, отдав участнику В Х⁰_АХ^D_А единиц блага X и получив от него Y⁰_BY^D_B единиц блага Y, останется на прежней кривой безразличия U⁰_A, на которой он был и до обмена, т.е. не улучшит, хотя и не ухудшит своего положения. Итак, при переходе от первоначального положения Z⁰ в положение D весь выигрыш от обмена достается участнику А. Но если бы участники перешли в положение, характеризуемое точкой R, то весь выигрыш от обмена достался бы участнику А (проделайте эти рассуждения самостоятельно).

При исходном распределении Z⁰ ни одна точка на контрактной кривой АВ, лежащая ниже и левее D или выше и правее R, не может характеризовать результатов добровольного и взаимоприемлемого обмена благами X и У между участниками А и В. Все точки контрактной кривой ниже и левее D принадлежат кривым безразличия участника А, приносящим меньшую полезность, чем U⁰_A, а все ее точки, расположенные выше и правее D, принадлежат кривым безразличия участника В, приносящим меньшую полезность, чем U⁰_B.

Итак, при исходном их распределении Z⁰, добровольный и взаимоприемлемый обмен между участниками существует лишь при распределении благ X и Y, представленном точками в интервале DF контрактной кривой АВ. При таком распределении взаимовыгодные сделки отсутствуют. Такое распределение является эффективным по Парето. Это такое распределение, при котором:

• не существует способа повысить благосостояние всех участников обмена;

• или не существует способа повысить благосостояние одного без снижения благосостояния другого;

• -или все выгоды от обмена исчерпаны;

• -или отсутствует возможность совершения взаимовыгодных сделок и т.д.

Для того, чтобы определить конкретную точку на отрезку DR, характеризующую конечное распределение благ X и У, при котором обмен ими между участниками А и В прекратится, введем кривые предложения благ к обмену из наличного запаса.