6.4.3. Ценовая олигополия

В отличие от количественных моделей олигополии, в которых фирмы выбирают объем выпуска, а отраслевая цена определяется в соответствии с обратной функцией рыночного спроса.

Рассмотрим теперь модели олигополии, ориентированные на цену как стратегическую переменную. В них фирмы устанавливают цену и реализуют по ней определенный рыночным спросом объем выпуска.

Модель олигополии Бертрана

Французский математик Жозеф Бертран ( 1883 г. ) в качестве альтернативы дуополии Курно предложил свою модель дуополии.

Он исходил из тех же предпосылок, которые сделал Курно (отсутствие сговора, однократность взаимодействия, однородность продукта, наличие неизменных и равных предельных издержек у фирм, закрытый вход).

Но в качестве стратегической переменной выступает цена, а не объем выпуска. Причем цену определяет каждый из дуополистов Бертрана, считая выбор соперника неизменным.

Пусть в отрасли действуют всего 2 фирмы, производится однородный продукт с одинаковыми и неизменными предельными издержками.

Предположим для простоты, что функция спроса - линейна:

Q = q₁ + q₂ = a / b – 1 / bP) (6.56)

В этом случае спрос на продукцию каждой из фирм зависит от цен на товар. Если цена, назначенная фирмой 1, превысит цену, назначенную фирмой 2, то никто не захочет покупать продукцию у фирмы 1.

b

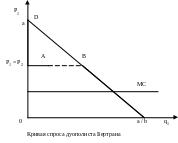
Рис. 6.18. Кривая спроса дуополиста Бертрана

Если эта цена снизится до Р₂, то поскольку выпускается одинаковая продукция, покупатели обоих фирм смогут удовлетворить за счет продукции каждой из фирм половину своего спроса.

Если же Р₁ хотя бы незначительно снизится по сравнению с Р₂, покупатели полностью переключатся на продукт фирмы 1 (при этом предполагается, что каждая фирма имеет такие производственные мощности, которые в состоянии обеспечить рыночный спрос в полном объеме).

Таким образом, кривая спроса на продукцию фирмы 1 состоит из трех отрезков ( рис. 6.6):

d₁(Р₁, Р₂) = 0, если Р₁ > Р₂ (отрезок аР₂ )

d₁(Р₁, Р₂) = D(p₁)/2, если Р₁ = Р₂ (т. А )

d₁(Р₁, Р₂) = D(p₁), если Р₁ < Р₂ (отрезок Bb ). (6.57)

Также будет выглядеть и функция спроса для фирмы 2.

Каждой фирме выгодно назначить цену чуть-чуть ниже конкурента. Тогда фирма, снизившая цену первой, сможет захватить весь рынок, поскольку продукция однородная, а потребители ведут себя рационально и выбирают при прочих равных тот товар, который дешевле. Предполагая (в соответствии с допущениями модели), что объявленные соперником цены неизменны, эта фирма фактически становится монополистом, захватывает весь рынок.

Но фирма-конкурент, оставшись без покупателей, вынуждена будет тоже снизить цену, причем несколько сильнее, чем это сделала первая фирма. Тогда все покупатели перейдут ко второй фирме.

Теперь первая фирма, столкнувшись с проблемой реализации продукции, снизит цену еще больше и т.д.

Таким образом, модель Бертрана является моделью "ценовой войны" в дуополии. Равновесие будет достигнуто лишь при снижении рыночной цены до уровня, ниже которого ее опускать уже нецелесообразно, т.е. до уровня предельных издержек. Поскольку МС=соnst, то МС=АС (предельные издержки равны средним).

Итак, в модели Бертрана результатом ценовой войны (при соблюдении всех вышеназванных предпосылок) становится объем производства, который производился бы и в условиях рынка совершенной конкуренции.

Изопрофиты у дуополистов Бертрана строятся в осях назначаемых фирмами цен (P₁, P₂) и являются не вогнутыми (как в дуополии Курно), а выпуклыми к соответствующим осям(рис.6.19). Такая форма изопрофит объясняет необходимость снижения цены каждым из дуополистов в ответ на снижение цены соперника, для сохранения уровень прибыли неизменным.

Если фирма 2 снизит цену с P₂ ¹ до с P₂ ^2,то фирма 1 должна снизить цену с P₁ ¹ до P₁², для сохранения на неизменном уровне прибыли П₁².

Если конкурент и дальше будет уменьшать цену, фирма 1 получит меньшую прибыль П₁¹, представленную более низкой изопрофитой ( рис. 6.19).

При такой форме изопрофит существует единственная цена для фирмы 1, которая, при существующей цене фирмы 2, дает максимум прибыли для фирмы 1 (различные такие сочетания значения цен обеих фирм представлены точками е₁, е₂, е₃, е₄, на рис. 6.19 а)

Кривые реакции фирм строятся путем соединения самых низких точек изопрофит (они же точки е). Кривые реакции представляют собой геометрическое место точек, соединяющих максимумы прибыли, которую получает каждая из фирм при назначении оптимальной цены (которая дает максимум прибыли) при заданном уровне цены конкурента.

Кривые реакции в модели Бертрана восходящие, т.к. прибыли дуополистов увеличиваются при повышении цен.

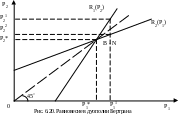
Точка пересечения кривых реакции является точкой равновесия по Бертрану- Нэшу (точка B-N на рис. 6.8). Она находится на луче под 45°, поскольку в равновесии фирмы установят одинаковую цену на уровне предельных издержек. Таким образом, равновесие по Бертрану является частным случаем равновесия по Нэшу

Е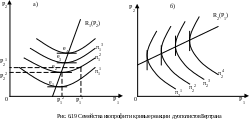 сли наклон кривой реакции фирмы 1 круче наклона кривой реакции фирмы 2, то равновесие по Бертрану устойчиво.

Пусть функция спроса на продукцию дуополиста Бертрана имеет вид:

d(P_i, P_j)=a_i-b_i P_i+ кP_j, где i,j = 1, 2, i ≠ j и а_i, b_i, к > 0. (6.58)

Предельные издержки составляют с_i, причем (с₁ = с₂).

Для того, чтобы вывести функцию реакции для дуополиста Бертрана, запишем его функцию прибыли:

П_i = (P_i - C_i)( a_i - b_i P_i + кP_j) = P_i a_i - C_i a_i - b_i P_i² + C_i b_i P_i + кP_j P_i - C_i кP_j) (6.59)

Необходимое условие максимизации прибыли:

∂ П_i / ∂P_i = a_i – 2b_iP_i + C_i b_i + кP_j= 0, (6.60)

отсюда функция реакции дуополиста Бертрана RF_i.:

P_i = (a_i + C_i b_i ) / 2 b_i + (к / 2 b_i) P₂ = A_i +B_iP_j (6.61)

где A_i = (a_i + C_i b_i ) / 2 b_i , . B_i=(к / 2 b_i) (6.62)

Функции реакции дуополистов Бертрана – линейны (т.к.. ∂ P_i / ∂P_j = 0 ), имеют положительный наклон ( рис. 6.19 и 6.20) и пересекаются в точке равновесия Бертрана –Нэша, точке B-N с координатами ( Р^В₁, Р^В₂ ),

при Р^В₁ = (A_i + A_j B_i) / (1 - B_i B_j). (6.63)