6.14. Кривые реагирования в модели Курно и контрактная кривая

Максимизация прибыли фирмой-дуополистом Курно не приводит к максимизации прибыли отрасли в целом..

Докажем это. Построим контрактную кривую, которая соединит точки касания изопрофит ( кривая Е₁Е₂ на рис. 6.15, 6.14).

6.15. Изопрофиты и контрактная кривая

Контрактная кривая соединяет все точки касания изопрофит, т.е. оптимальные точки, характеризующие максимальную совокупную прибыль отрасли.

В любой точке отрезка Е₁Е₂ контрактной кривой, отсекаемого изопрофитными линиями, проходящими через C -N, совокупная отраслевая прибыль выше, чем в точке C-N. При этом в точке Е₁ фирма 1имеет ту же прибыль (П₃¹) что и в точке С-N, а фирма 2 — большую (П₂²> П₃²); в точке Е₂ фирма 2 имеет ту же прибыль (П₃²), что и в точке C-N, а фирма 1 — большую (П₂¹ > П₃¹); в точках же между Е₁ и Е₂ обе фирмы будут получать прибыль большую, чем в C^N. Парадокс модели Курно заключается в том, что фирмы в итоге приходят к неоптимальному, с позиции максимизации совокупной прибыли, результату.

Объяснить этот парадокс можно, вспомнив о тех допущениях, которые мы делали при построении модели. Мы считали, что фирмы имеют возможность лиши однократного взаимодействия, поэтому они могут учиться на прошлом опыте. Каждая из фирм действует независимо — не зная о том, что соперник руководствуется тем же самым предположением в отношении ее поведения, что и она — в отношении него.

Модель Курно в случае n фирм.

Теперь рассмотрим олигополистическую отрасль, в которой действуют n фирм с такими же функциями издержек, что и в случае дуополии.

В случае n фирм Q = q₁ + ... + q_i + ... + q_n, функция прибыли для i-й фирмы:

П_i= (а - bQ)q_i - ТС -= (а – bq₁ - ... – bq_i- ... – bq_n) bq_i -TCi

Необходимое условие максимизации прибыли:

а – bq₁ - ... – bq_i - ... - bq_n - с = 0. (6. 28)

Отсюда:

q_i = ((а-с) / 2b) – (q₁ + … + q_{i –1} + q_{i +1} + … + q_n) / 2 (6.29)

Поскольку функции реакции у всех фирм симметричны и значения выпусков, максимизирующих прибыль, одинаковы (q₁= …= q_i-= ... = q_n), можно заменить каждое из (n - 1) значений выпуска в уравнении (6.29) на q_i, получив:

q_i = ((а-с) / 2b) –((n - 1) q_i / 2). (6.30)

откуда

q_i = (а-с) / b(n + 1) (6.31)

Равновесный отраслевой выпуск в случае n фирм составит:

Q* = n q_i* = (n(а-с) / b) •(n / (n + 1)) (6.32)

По мере увеличения числа фирм n в олигополии Курно отраслевой выпуск будет расти (величина n / (n + 1) тоже растет, стремясь к 1), а цена — снижаться, т.е. исход в пределе, при n→∞, будет бесконечно приближаться к совершенно конкурентному.

(См. Приложение 1)

Модельь Чемберлина

В Модели Чемберлина (1956г.) в отличие от модели Курно дуополист предполагает, что уровень выпуска конкурента изменяется в ответ на его решения. В итоге дуополисты, не вступая в тайный сговор, выберут для себя наиболее выгодные для себя решения (рис.6.16 ). Примем, что МС₁=МС₂=0

Первый шаг. Пусть первая фирма ведет себя как монополист. Максимизируя прибыль она выберет объем производства и цену:

q₁=Q_m=(а-с)/2b (6.33)

Р_m==(а+с)/2 (6.34)

При этом прибыль составит:

П₁= (а – с)²/4 bq (6.35)

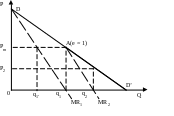
Рис. 6.16 Модель олигополии Чемберлина (простейшая версия)

Второй шаг. Вторая фирма, принимая решение, исходит уже из остаточной функции спроса АD’, считая что выпуск первой фирмы не изменится. Вторая фирма на остаточном спросе также принимает решение как монополист. Остаточную функцию спроса можно рассмотреть как функцию рыночного спроса, но только в новой системе координат, смещенной по отношению к первоначальной на q₁. Уравнение остаточной функции спроса:

Р’=(а+с)/2-bq₂ (6.36)

Максимизируя прибыль вторая фирма будет производить ровно половину от монопольного выпуска первой фирмы:

q₂=(а-с)/4b (6.37)

В итоге при снижении цены до:

Р=(а+3с)/4 (6.38)

отраслевой объем выпуска составит:

Q=3(а-с)/4b (6.39)

Поскольку уже в результате второго шага рыночная цена снизилась, прибыль первой фирмы составит всего лишь половину от первоначальной монопольной прибыли:

П₁= (а – с)²/8 b, (6.40)

а у второй фирмы – еще меньше:

П₂= (а – с)²/16 b. (6.41)

Третий шаг. Первая фирма, понимая, что вторая фирма реагирует на ее действия, сокращает свой объем производства вдвое (на размер выпуска конкурента), желая оставить монопольную цену Р_m=(а+с)/2.

Четвертый шаг. Вторая фирма, понимая, что ей выгоднее принять условия, предложенные первой фирмой, оставит свой объем производства неизменным, но будет продавать его по цене Р_m=(а+с)/2, которая выше его первоначальной цены.

В результате дуополисты поделят рынок поровну:

q_i = q₂ = (а-с)/4b (6.42)

и получат равную прибыль

П₁= П₂= (а – с)²/8 b, (6.43)

разделив монопольную прибыль между собой поровну.

Поскольку мы предположили существование линейной функции спроса р=а-2bQ и однородность выпускаемой продукции (поэтому q₁=q₂=q), то функция спроса примет вид:

р=а-2bq (6.44)

А поскольку мы считали, что издержки равны, то функция прибыли:

П= а q– 2bq^{2 -}сq, (6.45)

Необходимое условие максимизации прибыли:

dП/dq= а – 4bq - с=0 (6.46)

Достаточное условие максимизации прибыли

d²П/d²q= – 4b<0 (6.47)

Вывод: если выполняются предпосылки о равных издержках и однородности продукции, то фирмы в модели Чемберлина не вступая в тайный сговор, установят на рынке монопольную цену.