Пространственная ценовая дискриминация

Если между рынками существует значительное расстояние и высокая стоимость транспортировки, то фирмы могут осуществлять пространственную ценовую дискриминацию. Для этого фирма устанавливает разные цены для покупателей, в зависимости от их местоположения от места продаж.

Пример. Пусть завод монополиста располагается в городе Х и обслуживает рынок в городах Х иY.Будем считать, что число потребителей в этих городах одинаково. Обратные функции спроса на продукцию монополиста в городах Х и Y составляет Рх = D(Qх) и Р_Y = D(Q_Y), а издержки МС = SATC = const. Раз завод находится в городе Х, транспортными расходами внутри города можно пренебречь, а затраты на транспортировку каждой единицы продукции потребителям в город Y примем равными t.

Общая прибыль монополиста от реализации товаров в обоих городах:

π = D(Qх)Qх + [D(Q_Y)- t] Q_Y (5.28)

- где D(Qх)Qх- общая выручка от продажи Qх единиц продукции в городе Х, или TRх(Qх);

[D(Q_Y)- t]Q_Y — чистая, за вычетом расходов по доставке, выручка от продажи Q_Y единиц продукции в город Y , или TR_Y(Q_Y);

c(Q_Х+Y), — затраты на производство всей продукции.

Пусть Р^-_Y (Q_Y)=D(Q_Y) – t - цена, которую получает монополист за каждую единицу товара, продаваемую в городе Y (за вычетом расходов на доставку, а Р_Y(Q_Y) = (Q_Y) – t обратная функция чистого спроса.

а)

б)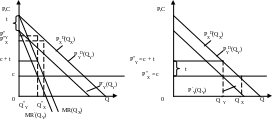

Рис. 5.20. Монополист, осуществляющий пространственную ценовую дискриминацию, в сравнении с совершенно конкурентным предприятием.

На нем показаны обратные функции спроса покупателей, размещенных в городах Х и Y (они одинаковы),т.е. (Рх = D(Qх)) = (Р_Y = D(Q_Y)) , а также функция нетто спроса покупателей, находящихся в городе Y, — P_Y(Q_Y).

Монополист должен распределить свой выпуск между городами Х и Y так, чтобы максимизировать общую прибыль. При этом он должен учитывать, что если P_B<P_A+t, то реализация приобретенного на дешевом рынке в городе Х товара на более дорогом рынке в городеY с учетом затрат на перевозку окажется невыгодной для перепродавцов. Максимизация прибыли предполагает выполнение следующих условий:

dπ / dQ_Х =Q_Х(dP_Х/d_Х ) - D(Q_Х) - c = 0

dπ / dQ_Y =Q_Y(dP_Y/dQ_Y ) - D(Q_Y) - c – t = 0 (5.29)

или,

MR(Q_X) = c,

MR(Q_Y) - t = c.

Из (5.29) следует, что для осуществляющей пространственную ценовую дискриминацию фирмы прибыль будет максимальной при условии, что выполняется равенство

MR^-(Q_Y) = MR(Q_Y)- t = MR(Q_Х) = с, (5.30)

т. е. чистая предельная выручка в городеY должна быть равна предельной выручке в городе Х и он, в свою очередь, должны быть равны предельным издержкам с.

Оптимальные количества товара Q_X и Q*_Y , поставляемые в Х и Y назначаются так, чтобы предельная выручка в городе Y превышала предельную выручку в городе Х на величину транспортных расходов t, т. е. должно выполняться равенство:

MR(Q*_Y)- t = MR(Q*_Х) (5.31)

При линейной функции спроса наклон графика предельной выручки вдвое круче наклона соответствующего графика спроса, поэтому разница цен Р*_Х и Р*_Y меньше транспортных расходов, t, или Р_Y < Р*_X + t.,т.е.

учитывая расходы на транспортировку, никто не может получить прибыль, закупая товар на дешевом рынке и перепродавая его на дорогом. Из этого следует, что в том городе, где производится продукция цены будут назначены выше, т.е. монополист, осуществляющий пространственную ценовую дискриминацию, «дискриминирует против» покупателей, живущих рядом. А цена, по которой реализуется продукция в расположенном в городе Y более чем на t ниже цены в городе Х, где это благо производится.

Итак, при пространственной ценовой дискриминации разница в ценах не равна величине транспортных расходов, т.е. чистая цена (без стоимости транспортных расходов) за единицу товара, продаваемую на отдаленном рынке, ниже.

Для совершенно конкурентной фирмы цена будет одинаковой и в городе Х и в городе Y (рис.5.20 б). Цена в городе Х равна неизменным предельным затратам, Р*_Х = МС = с , а в городеY- равна предельным затратам, но с включением в них транспортных расходов: Р*_Y = МС⁺ = с +t. Но это и значит, что нетто цены, очищенные от транспортных расходов, были бы одинаковы и равны предельным затратам на производство продукции:

P^-_Х= P^-_Y= c = мс,