1.6. Правильные способы рассуждений, основанные на теории силлогизмов

Плодотворной почвой на целых 25 веков для поиска всевозможных форм правильных рассуждений явилась силлогистика Аристотеля. Чтобы рассмотреть её основные аспекты нам необходимо возвратится к понятию суждения (высказывания) и рассмотреть некоторые его стороны более детально.

Все суждения обладают количественной и качественной характеристиками. Простейшие суждения состоят из субъекта, связки, предиката (сказуемого) и кванторного слова: S есть P или S не есть P. S – субъект, P – предикат. Связка, как в данном случае, может быть выражена одним словом – есть, не есть, или словом суть, является, или группой слов и даже просто тире. Перед субъектом суждения может стоять кванторное слово: все, некоторые, ни один и др. Кванторное слово указывает, относится ли суждение ко всему объему понятия, выражающего субъект, или к его части.

Количественная характеристика суждения зависит от того, обо всех ли предметах данного множества, о части предметов этого множества или об одном предмете идет речь в субъекте, суждения делятся на общие, частные и единичные. Например: «Все тигры – хищники» – общее суждение; «некоторые люди – левши» – частное; «Везувий – действующий вулкан» – единичное;

Качественная характеристика суждения определяется тем, что утверждающая, отрицающая используется связка или утверждающий, отрицающий предикат.

В связи с этим в формальной логике используется объединенная классификация суждений по количеству и качеству, на основе которой выделяются следующие 4 типа суждений:

• Общеутвердительные суждения – их обозначают буквой А, а их форма: «Все S есть P .»

• Частноутвердительные суждения - их обозначают буквой I, а их форма: «Некоторые S есть P.»

• Общеотрицательные суждения – их обозначают буквой Е, а их форма: «Ни одно S есть P.»

• Частноотрицательные суждения – их обозначают буквой О, а форма: «Некоторые S не есть P». Например: «Некоторые спортсмены-олимпийцы не являются Олимпийскими чемпионами».

Условные обозначения (E и O)для отрицательных суждений происходят от гласных букв слова nego, что означает отрицаю.

В формальной логике большое количество правильных форм рассуждений делается на основе непосредственных дедуктивных умозаключений из одной посылки. Особый мировоззренческий интерес представляют умозаключения по так называемому логическому квадрату. Вершины логического квадрата соответствуют четырем типам простых категорических суждений. При этом левая верхняя и правая верхняя вершины соответствуют суждениям A и E, а нижняя левая и нижняя правая вершины соответствуют суждениям типа I и O. Стороны логического квадрата и его диагонали указывают на отношение логического подчинения отмеченных суждений.

С учетом сказанного логический квадрат представляют обычно в таком виде (рис. 1)

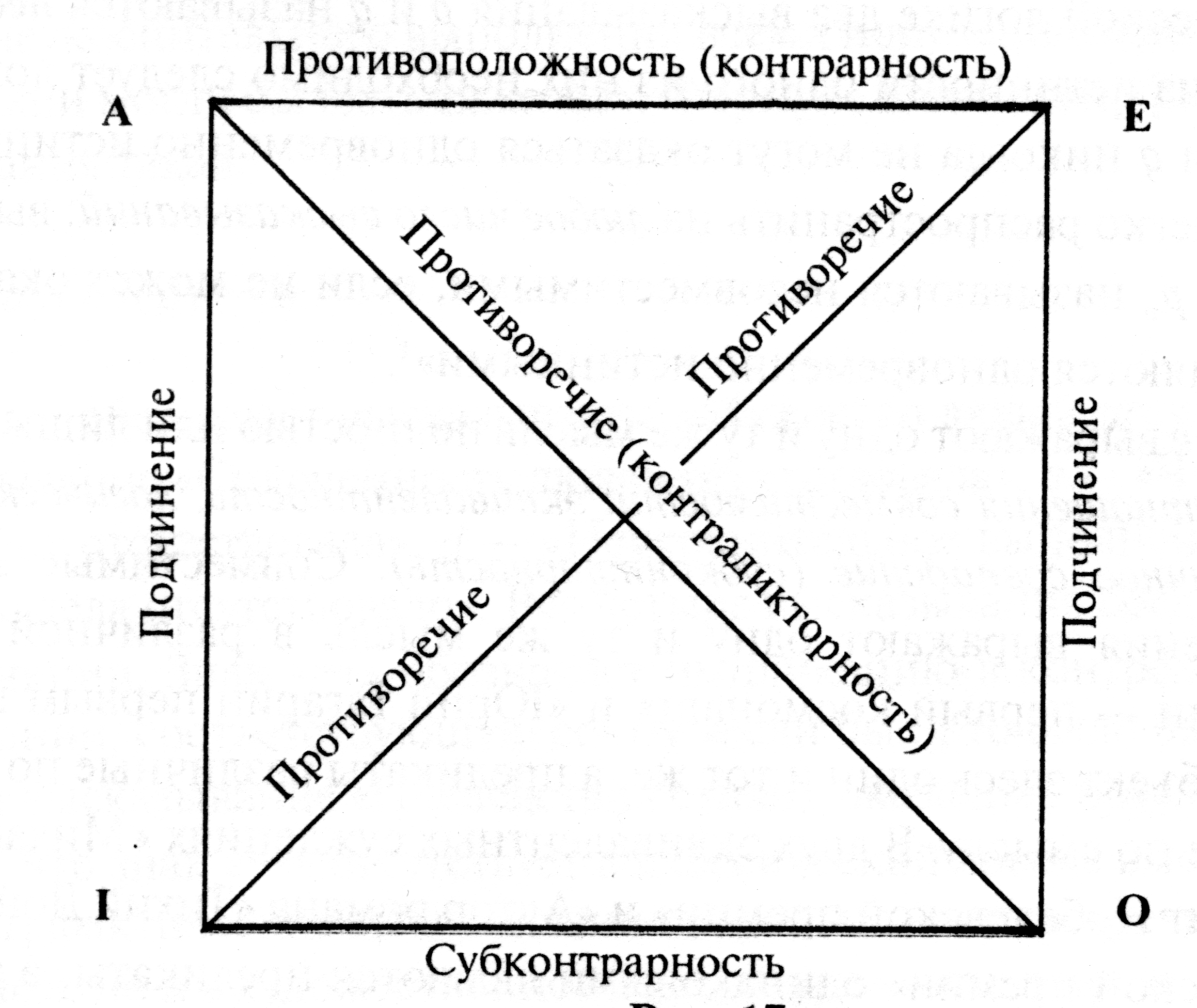
Рис. 1.

Логический квадрат способствует запоминанию различных логических отношений (служит мнемоническим целям), которые существуют между высказываниями типов A, E,I и O с одинаковым расположением терминов, т.е. с одинаковыми субъектами и одинаковыми предикатами.

Приведем примеры всех 4-х типов суждений с одинаковыми субъектами и предикатами, и рассмотрим отношения между такими суждениями.

A – «Все свидетели дают истинные показания»;

Е – «Ни один свидетель не дает истинных показаний»;

I – «Некоторые свидетели дают истинные показания»;

O – «Некоторые свидетели не дают истинных показаний».

Если все эти суждения соотнести с логическим квадратом, то нетрудно заметить, что из истинности общеутвердительного суждения A следует истинность частноутвердительного, подчиненного ему суждения I, а из истинности общеотрицательного суждения E следует истинность частноотрицательного суждения O.

Относительно противоречащих суждений (они расположены на противоположных концах диагоналей «логического квадрата») A – O и E – I можно сделать такое заключение: если одно из них истинно, то другое будет обязательно ложным. Из этого следует, что они находятся под действием закона исключенного третьего.

Рассмотренные выше заключения были однопосылочными. Однако в практике логических рассуждений большее значение имеют двухпосылочные заключения, в которых от наличия некоторых отношений меду парами терминов: S и M, P и M, фиксируемых в посылках, приходят к заключению между терминами S и P. Такие заключения называются простыми категорическими силлогизмами.

Примером простого категорического силлогизма является умозаключение:

Слово «бег» обозначает действие.

Некоторые существительные обозначают действие.

Слово «бег» – существительное.

Он состоит из трех суждений: первые два являются посылками, а последнее – заключением. Общим термином является словосочетание «слово «бег»», связывающее термины посылок – «существительное» и «обозначает действие».

В простом силлогизме выделяют больший термин P – это предикат заключения в приведенном примере – «обозначают действия»), меньший термин S (в приведенном примере – «существительное». Термин же, являющийся общим для обеих посылок (его обозначают буквой M), называют средним термином (в приведенном примере это словосочетание «слово бег»»).

Далее, посылку, содержащую меньший термин, называют меньшей посылкой, а посылку, содержащую больший термин – большей посылкой. Принимают также условие, что большую посылку всегда помещают на первое место, а под ней записывают меньшую посылку.

При этих условиях все простые категорические силлогизмы можно разделить на так называемые фигуры. Каждая фигура определяет множество простых категорических силлогизмов, имеющих одну и ту же структуру, определяемую расположением среднего термина в посылках.

Таких фигур возможно всего четыре – рис. 2.

Фигура I Фигура II Фигура III Фигура IV

1 . М P 1. P M 1. M P 1. P M

2. S M 2. S M 2. M S 2. M S

3. S – P 3. S – P 3. S – P 3. S – P

Рис. 3.

На всех фигурах рис. 3 цифрой 1 обозначена большая посылка, цифрой 2 – меньшая посылка, а цифрой 3 – заключение. Буква S обозначает меньший термин, буква P – больший , а буква M – средний термин.

Если в некоторой фигуре указать конкретно тип суждений, стоящих на местах посылок и заключения, то получим разновидность данной фигуры. Так, если в фигуре I положить, что большая посылка, меньшая посылка и заключение – это суждения типа A, то получим такой силлогизм:

1. Всякий M есть P

2. В сякий S есть M

3. Всякий S есть P.

Такого рода разновидности фигур называются их модусами. В каждой фигуре имеется 64 модуса, а во всех четырех фигурах их будет 256. Однако не во всех модусах заключение логически следует из посылок, т.е. оно не будет истинным. Поэтому правильными модусами будут только те из них, для которых имеет место логическое следование. А таких правильных модусов существует всего 24.

Для того чтобы правильные модусы было легче запомнить в средневековье для них придумали специальные словесные названия. Причем эти названия таковы, что все гласные буквы в них, идущие слева направо, соответствуют типу суждения большей посылки, меньшей посылки и заключению. Так, приведенный выше модус фигуры I называется Barbara, что соответствует типам суждений большой, малой посылок и заключения AAA.

При изучении логики средневековым студентам приходилось буквально «зазубривать» наименования этих модусов. Чтобы иметь представление насколько это было нелегко, приведем названия 24-х правильных модусов из всех четырех фигур.

Фигура I	Фигура II	Фигура III	Фигура IV
Barbara (AAA)	Baroko (AOO)	Bokardo (OAO)	Camenos (AEO)
Celarent (EAE)	Cesare (EAE)	Disamis (IAI)	Dimaris (IAI)
Darii (AII)	Camestres (AEE)	Datisi (AII)	Camenes (AEE)
Ferio (EIO)	Festino (EIO)	Ferison (EIO)	Fresison (EIO)
Barbari (AAI)	Camestrop (AEO)	Daparti (AAI)	Bramantip (AAI)
Celaront (EAO)	Cesaro (EAO)	Felapton (EAO)	Fesaro (EAO)

Приведем в качестве примера для каждой из 4-х фигур категорических силлогизмов по одному модусу.

Фигура I

Все жидкости (M) теплопроводны (P).

Вода (S) – жидкость (M).

Вода(S) – теплопроводна (P).

Фигура II

Все ужи (P) – пресмыкающиеся (M).

Это животное (S) не является пресмыкающимся (M).

Это животное (S) не является ужом (P).

Фигура III

Все углероды (M) – простые тела (P).

В се углероды (M) – электропроводны (S).

Некоторые электропроводники (S) – простые тела (P).

Фигура IV

Все киты (P) – млекопитающие (M).

Н и одно млекопитающее (M) не есть рыба (S).

Ни одна рыба (S) не является китом (P).

Нетрудно убедиться, что фигура I соответствует модусу AAA, фигура II – модусу AEE, фигура III – модусу AAI, а фигура IV соответствует модусу AEE. Все приведенные умозаключения правильные, так как они входят в группу из 24-х правильных модусов.

Подводя итог краткому рассмотрению некоторых сведений из формальной логики, можно отметить следующее. Формальная логика знакомит с правилами различных видов умозаключений. Она дает в руки инструмент, который позволяет всегда получать истинное логическое следствие (заключение – высказывание) из истинных посылок. Если же при истинных посылках получаются ложные заключения, то значит, были применены неправильные формы умозаключений.

Поскольку предметом данного пособия является математическая логика, то следует указать два момента:

1. Используя аппарат математических преобразований, математическая логика позволяет во многих случаях из данной информации получить новые истинные сведения, непосредственно не очевидные для формальной логики, но заключенные в этой информации.

2. Для специальностей направления «Информатика и вычислительная техника» курс математической логики и теории алгоритмов не является обычным общеобразовательным курсом. Он является одной из тех специальных дисциплин, знания которой необходимы для решения задач создания систем искусственного интеллекта.