Раздел 2

Подраздел 2.1

1. Формулами являются предложения 1), 3), 4), 6) и 7).

2. 1) ; 3) ; 4) нельзя упростить;

6) ;

7)

Подраздел 2.4

1. 1) Применим подстановку , получим .

2) Применим подстановку к аксиоме

, получим .

3) Применим подстановку к аксиоме , получим

├ .

4) Применим подстановку к аксиоме

, получим ├ .

5) Применим подстановку к аксиоме

, получим ├ .

2. 1) Для аксиомы сделаем подстановку

, получим доказуемую формулу

├ . (1)

Но в подразд. 2.3 мы доказали, что

├ (2)

Применяя к формулам (2) и (1) ПСЗ, получим ├ .

2) Возьмем аксиому и сделаем в ней подстановку

. Получим

├ . (1)

Но ├ . (2)

Применяя к (1) и (2) ПЗС, получим ├ .

3) К аксиоме применим подстановку

, получим

├ , (1)

но на основании аксиом и

├ , (2)

├ . (3)

Применяя к (2), (3) и (1) ПСЗ, получим

├ .

4) К аксиоме применим подстановку

, получим

├ . (1)

Но на основании аксиом и

├ или ├ ; (2)

├ или ├ . (3)

Применяя к формулам (1), (2) и (3) ПСЗ, получим

├ .

5) К аксиоме применим подстановку

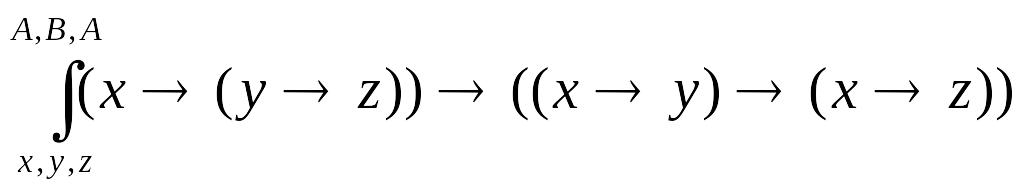, получим

├ . (1)

Но на основании аксиомы

├ . (2)

Из (1) и (2) по ПЗ получим ├ .

3. В аксиоме сделаем подстановку

, получим

├ . (1)

Возьмем аксиомы и и применим к ним сначала правило подстановки:

├

├ ,

а затем правило контрпозиции, получим

├ ; (2)

├ . (3)

Из (2), (3) и (1) по ПСЗ получим .

4. 1) По условию ├ . (1)

Используя аксиому , получим

├ . (2)

Применим к формуле (2) правило контрпозиции, получим

├ . (3)

Из формул (1) и (3) по ПЗ получим ├ .

2) Так как по условию ├ , (1)

то, используя аксиому , получим

├ . (2)

Из формул (1) и (2) по ПЗ получим ├ .

3) Так как по условию ├ , (1)

то, используя аксиому , будем иметь

├ . (2)

Из (1) и (2) по ПЗ получим ├ .

4) По условию ├ . (1)

Используя аксиому ├ , получим

├ . (2)

Применим к формуле (2) правило контрпозиции, получим

├ . (3)

Применяя к формулам (1) и (3) ПЗ получим ├ .

Подраздел 2.8

1. 1) Запишем вывод из . Последней формулой в выводе является , значит, она выводима из .

2) Запишем вывод из :

[эта формула получена из аксиомы заменой на и на ], [эта формула получена из аксиомы заменой на , на и на ], . Последней формулой в выводе является , значит, она выводима из .

3) Запишем вывод из [эта формула получена из аксиомы заменой на и на ], . Последняя формула выводима из .

4) Запишем вывод из [эта формула является аксиомой ], . Последняя формула выводима из .

5) Сначала докажем, что для ├ .

После этого, применив теорему дедукции, получим искомый результат. Запишем вывод из [последняя формула получается как вывод из , доказательство которого было приведено в 2.5].

Тогда по правилу дедукции , что и требовалось доказать.

6) Запишем вывод из :

[для получения этой формулы используем закон перестановки посылок], . Последняя формула выводима из .

7) Сначала докажем, что

├ . (1)

Для этого докажем, что из ├ . Запишем вывод из [аксиома ], . Отсюда, согласно обобщенной теореме дедукции, справедлива запись (1). Теперь докажем исходное выражение. Запишем вывод из H:

[получается из аксиомы заменой на , на и на ], [аксиома ], [получается по ПСЗ из 3-х предыдущих формул]. Таким образом, получили, что последняя формула выводима из .

Примечание. При записи некоторых выводов в предыдущих задачах в квадратных скобках давались пояснения о том, как получена та или иная формула.

2. 1) Возьмем совокупность формул и покажем, что . Для этого запишем вывод из : .

Так как формула является последней в выводе, то . Тогда согласно ОТД . Можно было бы вывод не проводить, а сразу сделать заключение, что доказуема исходная формула, так как она является аксиомой .

2) Возьмем совокупность формул и покажем, что . Для этого запишем вывод из : . Формула является последней в выводе, поэтому .Тогда согласно ОТД .

3) Так как исходная формула является аксиомой , то она, так же как и формула из примера 1), является доказуемой по определению, а значит, вывод можно не записывать.

4) Возьмем совокупность формул и покажем, что . Запишем вывод из тогда согласно ОТД из того, что следует: .

5) Для совокупности формул покажем, что . Для этого запишем вывод из [последняя формула получена как вывод , доказательство которого было приведено в 2.5]. Тогда согласно ОТД из того, что следует .