«Все s есть p»,

несмотря на то, что в этих суждениях совершенно разное содержание.

В приведенной форме S – понятие, соответствующее рекам, коровам и зебрам из приведенных выше суждений а P – это то, что утверждается о понятии (сказуемое, иначе – предикат – по латыни).

Приведем два других суждения:

• Если металл нагревать до определенной температуры, то он плавится;

• Если человек владеет одним иностранным языком, то второй иностранный язык осваивается значительно быстрее;

Форма обоих этих суждений одна и та же, но она отличается от предыдущей формы и имеет вид:

«Если s есть p, то s есть p1».

Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы получаем новое суждение – заключение. Умозаключение является простейшей разновидностью более сложного процесса мышления – рассуждения. В ходе рассуждения могут осуществляться несколько умозаключений.

Современная формальная логика для записей умозаключений использует следующую схему

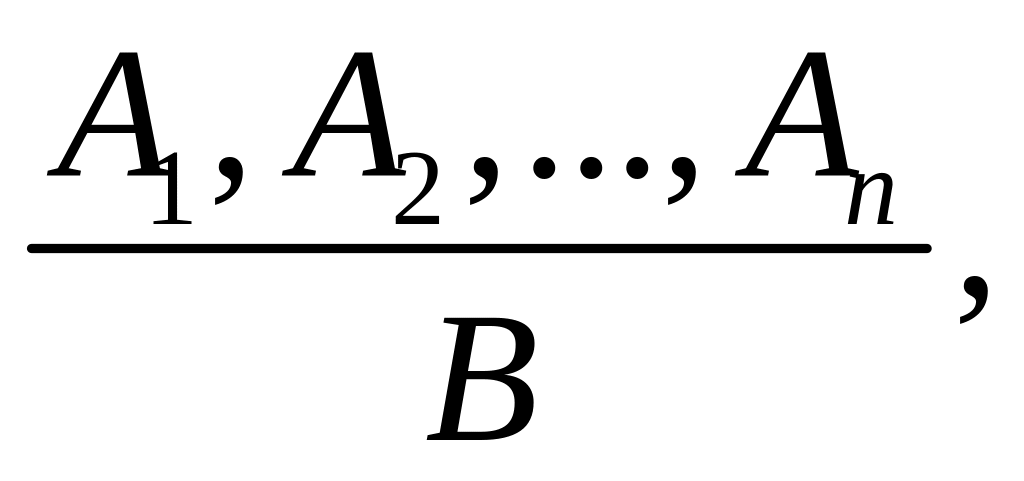
где над чертой записываются посылки, под чертой – заключение, а сама черта выражает процесс выведения заключения из посылок.

Из приведенных формулировок суждения и умозаключения видим, что и то, и другое представляет форму мышления. Но формы эти различны. Суждение проще по форме, в нем что-либо утверждается лишь в одном понятии. В умозаключении участвуют от одного до нескольких суждений и некоторый процесс вывода. Для любого суждения характерно понятия истинности или ложности. Это определяется конкретным содержанием (смыслом) того или иного суждения. Если суждение верно отражает реальную действительность, то оно истинно, в противном случае оно ложно.

Для умозаключения (рассуждения) характерно понятие формальной правильности или неправильности. Рассуждения являются правильными, если соблюдаются законы логики. Но даже при правильных рассуждениях, т.е. при соблюдении правил логики в заключении можно получить как истину, так и ложь. Существует много видов умозаключений. В качестве примеров, рассмотрим наиболее часто встречающуюся форму умозаключения, которая даже при истинных исходных суждениях может приводить к ложному умозаключению.

1. Все металлы проводят электрический ток – истина.

Алюминий проводит электрический ток – истина.

Алюминий – металл – истина.

В этом примере из истинных посылок получилось истинное заключение.

2. Все металлы – твердые тела – ложь.

Ртуть не является твердым телом – истина.

Ртуть не является металлом – ложь.

Во втором умозаключении мы получили ложное заключение именно потому, что первая посылка была ложной.

3. Все металлы проводят электрический ток – истина.

Вода проводит электрический ток – истина._______

Вода – металл – ложь.

В третьем умозаключении из обеих истинных посылок мы получили ложное умозаключение. Почему это произошло? Из приведенных примеров ясно, что, рассуждая по такой форме, мы не всегда приходим к истинному заключению. Здесь заключение не следует с достаточным основанием из истинности первой посылки.

Таким образом, для получения истинных заключений по приведенной форме обе посылки должны быть истинными суждениями и соблюдаться правила и законы логики. При этим, как уже говорилось выше, нельзя отождествлять понятия: истинность и правильность, а также ложность и неправильность.

Приведенные формы абстрактного мышления являются основополагающими элементами формальной логики – науки о законах и формах правильного мышления. Предназначение логики – помогать доказывать истинные суждения и опровергать ложные. То же самое можно сказать иначе: задача логики состоит в том, чтобы ответить на вопрос, как мы должны мыслить, чтобы достичь цели познавательного процесса – получить истинные знания об исследуемых процессах и явлениях.

Основными формально – логическими законами являются:

1) закон тождества;

2) закон непротиворечия;

3) закон исключенного третьего;

4) закон достаточного основания.

Логические законы действуют независимо от воли людей (в отличие от законов общественных). Они являются отражением связей и отношений вещей материального мира. Логические законы носят общечеловеческий характер, поскольку во все исторические эпохи все люди мыслили по одним и тем же логическим законам. Под логическим законом в формальной логике понимается такая форма сложного высказывания, которая принимает истинное значение при любых логических значениях, входящих в него простых высказываний.

Следует обратить внимание, что приведенные законы в формальной логике составляют ее основу. Но кроме них существует еще большое число вспомогательных законов, число которых превышает несколько десятков.