1.6.2. Табличный метод минимизации
В этом методе два первых шага как бы объединены и выполняются с помощью специальной таблицы, называемой картой Карно (КК) или картой Карно-Вейча (еще иногда называемой диаграммой). Третий шаг выполняется так же, как и в расчетном методе. В принципе карта Карно является разновидностью табличной записи логической функции, заданной в СНДФ или в СНКФ, т.е. представляет разновидность таблицы истинности.
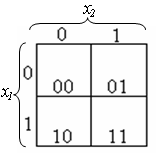
Для двух переменных КК представляет собой квадрат, разделенный на 4 клетки – по одной клетке на каждый набор переменных. Строки этой карты связываются с переменной , а столбцы – с переменной . Каждая клетка соответствует определенной конституенте, и ей присваивается свой порядковый номер, который представляет собой двоичное число, в разрядах которого записываются цифры (набор), находящиеся слева от клетки и сверху над ней. Фигурные
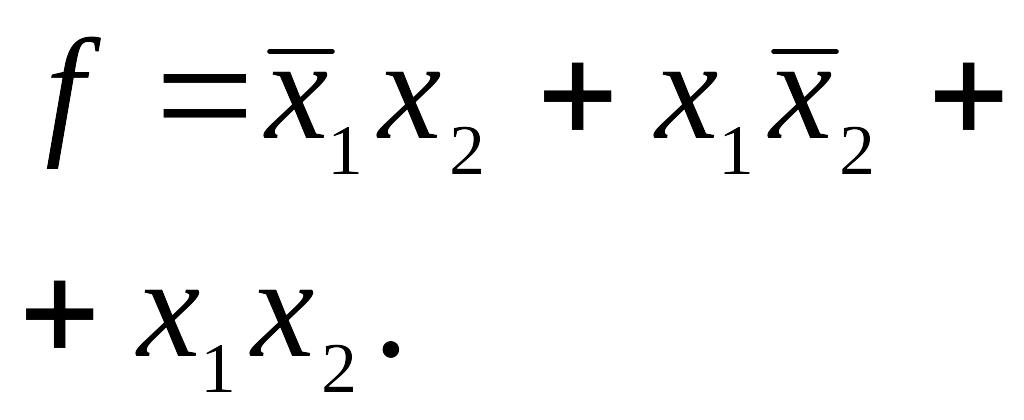
Рис.1
Рис. 2 Рис. 3
скобки указывают, каким переменным соответствуют строки и столбцы карты (рис.1).
Если при данном наборе, соответствующем номеру клетки, логическая функция равна 1, то единица записывается в эту клетку. Если логическая функция при данном наборе равна 0, то в клетку записывается 0 (или ничего не записывается).
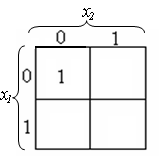
На рис.2 приведена
КК с одной заполненной клеткой, и
соответствующая этой карте логическая
функция будет
.
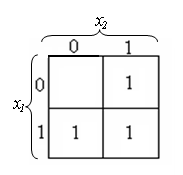
На рис.3 приведена карта с тремя
заполненными клетками, и ей будет
соответствовать функция
т.е. конституенты, соответствующие
заполненным клеткам в функции, соединяются
дизъюнкцией.
В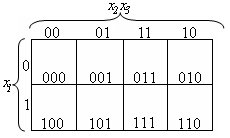
случае трех переменных КК содержит 8
клеток, и нумеруются они так, как показано
на рис.4. Номер каждой клетки получается
объединением всех цифр, находящихся
слева от клетки и сверху от нее.
С
Рис. 4
значением всего лишь одного разряда (переменной). Для этих целей используется не обычный двоичный код (тогда 3-й и 4-й столбцы на рис.4 были бы соответственно пронумерованы как 10 и 11), а двоичный отраженный код, первая половина которого получается обычным образом, а вторая половина – зеркальным отражением первой, но не всех ее разрядов, а только младших (правых), а в старшем разряде ставится единица. То есть процесс получения отраженных кодов мы можем представить так:
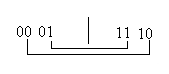
Для 3-разрядных двоичных чисел двоичный отраженный код формируется следующим образом:
Для четырех переменных КК содержит 16 клеток (рис.5).
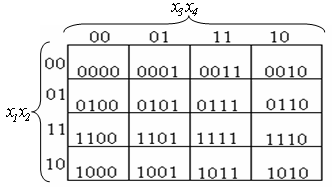
Рис. 5
Д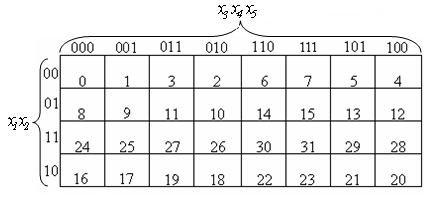
ля
пяти переменных необходимо иметь КК с
32 клетками. Эти 32 клетки можно представить
как 2 карты по 16 клеток или одну карту
на 32 клетки. Одна карта на 32 клетки будет
иметь такую нумерацию строк и столбцов
с учетом использования отраженных
кодов, которая показана на рис.6.
Рис. 6
В карте Карно,
изображенной на рис.6, нумерация клеток
дается в десятичной системе счисления.
Это позволяет производить очень
компактную запись логической функции.
Действительно, при записи логической
функции, можно указать большой знак
дизъюнкции
(применяемый аналогично знаку
или
в обычной алгебре), в скобках после него
перечислить те номера клеток, в которые
должна быть помещена 1. Такую запись
логической функции называют числовой.
Причем число клеток
в КК зависит от числа переменных m
и будет
определяться по максимальному номеру
клетки как
,
где
− ближайшая наибольшая целая часть
,
т.е.
,
а
−
максимальный номер клетки в такой
записи.
Например, если
логическая функция записана в виде
то это значит, что число клеток будет
,
т.е. число переменных будет 4, число
клеток будет
а единицы надо поместить в клетки с
номерами 0,1,3,4,6,9,11. В двоичной системе
счисления эти номера будут иметь вид:
0000,0001,0011,0100,0110,1001,1011. Тогда КК с отображенной
на нее приведенной функцией будет иметь
вид, представленный на рис.7.
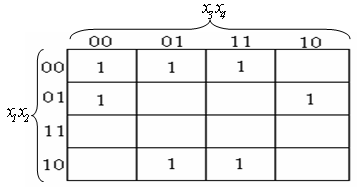
Рис. 7
Теперь приведем правила минимизации с помощью КК.
1.
соседних клеток, содержащих 1, и
расположенных по вертикали либо по
горизонтали в виде прямоугольника либо
квадрата (такую совокупность клеток
называют покрытием), соответствуют
одной импликанте, ранг которой
где
− число переменных, меньше ранга
покрываемых конституент на
единиц. Чем больше клеток в покрытии,
тем проще выражаемый этим покрытием
член логической функции − импликанта.
2. Импликанта, соответствующая некоторому покрытию заполненных единицами клеток, содержит символы тех переменных, значения которых совпадают у всех клеток, образующих покрытие. Причем символ берется с отрицанием, если для всех клеток покрытия он принимает значение 0, и без отрицания – в противном случае.
Пример.
Минимизировать логическую функцию
с помощью
КК. Минимизируемая функция будет состоять
из трех переменных, соответствующая ей
КК будет состоять из 8 клеток. Поэтому
КК, с отображенной на нее заданной
функцией в виде помеченных единицами
клеток и выделенных пунктирными линиями
покрытий, приведена на рис.8.
Покрытие 1
Покрытие 2
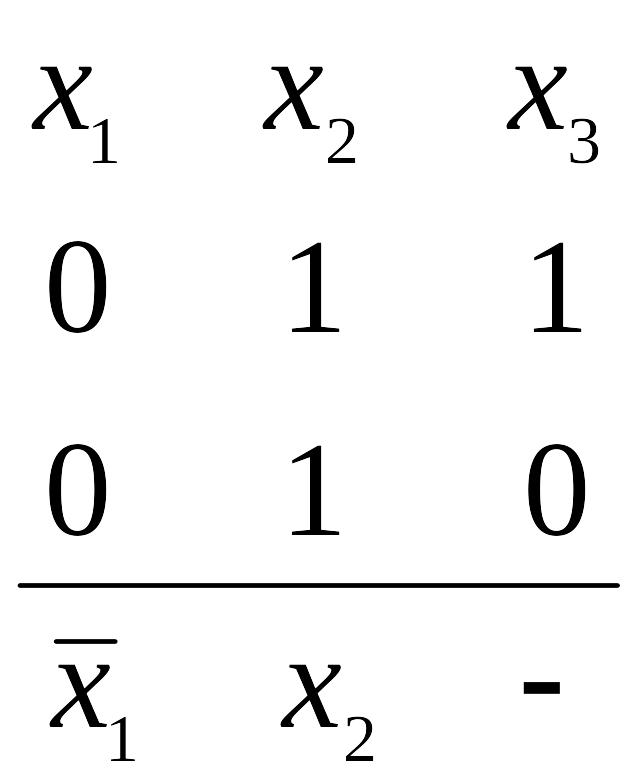
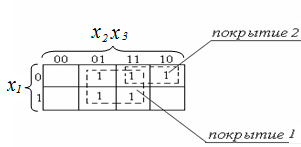
Рис.8
Следует отметить некоторые особенности работы с покрытиями. Каждое покрытие нужно использовать только один раз. Если КК свернуть в цилиндр вдоль горизонтальной или вертикальной оси, то будет видно, что крайние клетки тоже оказываются соседними и они могут образовывать покрытие. Такой характерный случай покрытий для КК на четыре переменные приведен на рис.9.
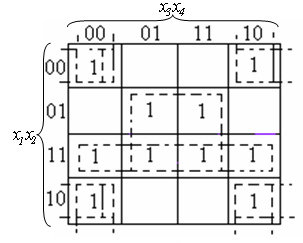
Рис. 9
Приведем еще один
пример КК с отображенной на нее логической
функцией, когда единицы находятся в
крайних клетках. Эта функция имеет вид
.
Соответствующая ей КК приведена на
рис.10.
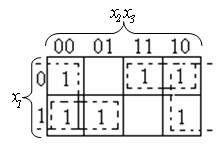
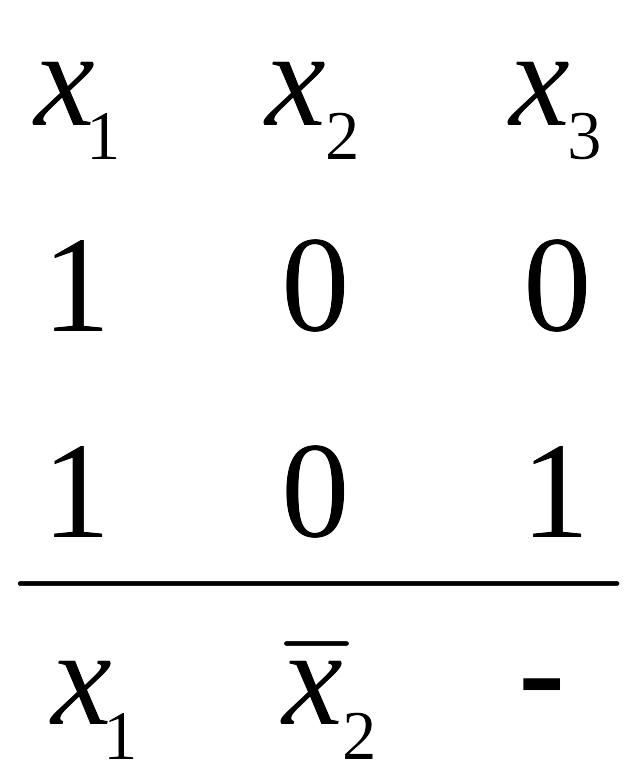
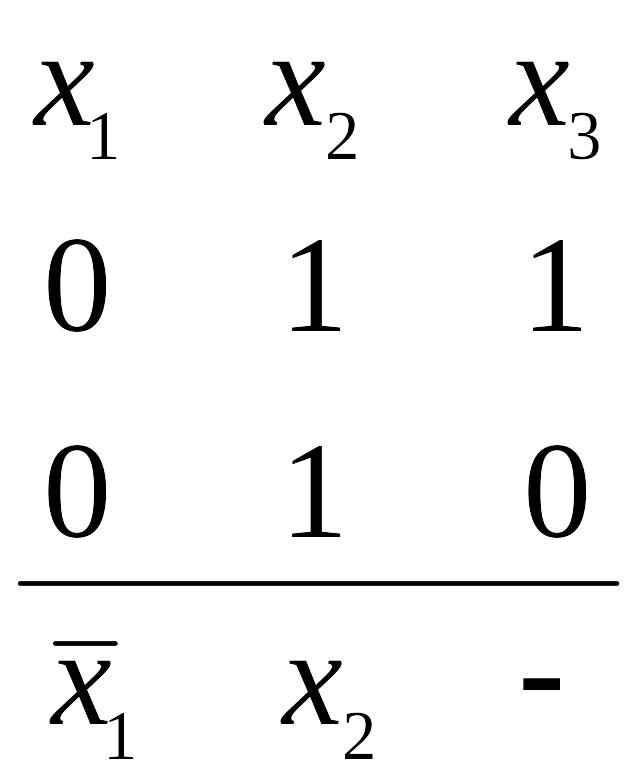
Рис. 10
Недостатком
рассмотренного метода считается то,
что при числе переменных
КК становятся громоздкими и неудобными
для практического применения. Однако,
справедливости ради, нужно отметить,
что сейчас уже имеются разработанные
компьютерные программы, минимизирующие
логические функции с 9 переменными.