6.Цільові навчальні завдання.

Приклади розв'язування задач

Порядок дій при виконанні цільових навчальних завдань на тему "Механічні коливання і хвилі":

1) Запишіть рівняння, яке задано в задачі і рівняння гармонічного коливання в загальному вигляді, зпівставте ці рівняння і визначить основні характеристики (зміщення, амплітуду, період, частоту, фазу) згідно умови задачі;

2) швидкість і прискорення матеріальної точки під час гармонічних коливань, а також максимальне значення цих величин, визначить із рівняння гармонічних коливань, параметри якого відповідають даним задачі;

3) період гармонічних коливань в різних ситуаціях визначайте за формулою 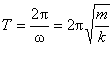, де  - циклічна частота коливань,  = k/m. Модуль прискорення точки, що коливається, a = kx/m, де x - зміщення точки із положення рівноваги.

4) Визначив прискорення із другого закону Ньютона, знайдіть коефіцієнт k, а потім період коливань;

5) якщо є значення кінетичної або потенціальної енергії для певного положення або часу для визначення параметрів коливальних процесів використовуйте закон збереження і перетворення енергії.

6.1. Яке рівняння відповідає гармонічним коливанням, частота яких дорівнює 0,5 Гц, амплітуда дорівнює 80 см, а початкова фаза дорівнює нулю?

ПРИКЛАД РОЗВ’ЯЗКУ

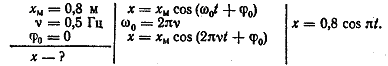
6.2. Яке рівняння відповідає гармонічним коливанням, частота яких дорівнює 0,5 Гц, амплітуда дорівнює 7 см, а початкова фаза дорівнює π /2 рад і при цьому за 2 хвилини здійснюється 240 коливань?

ПРИКЛАД РОЗВ’ЯЗКУ

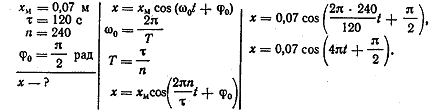
6.3. Яке зміщення математичного маятника (див. мал.) відповідає моментам часу, що дорівнюють Т/2 і Т, якщо маятник здійснює коливання з амплітудою 3 см при початковій фазі π рад?

ПРИКЛАД РОЗВ’ЯЗКУ

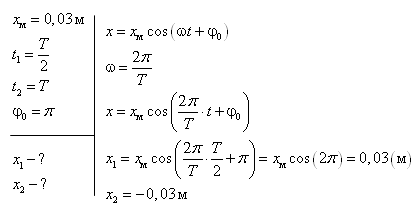
6.4. Який коефіцієнт затухань, якщо за t = 10 с амплітуда затухаючих коливань зменьшилася у е раз?

ПРИКЛАД РОЗВ’ЯЗКУ

Амплітуда затухаючих коливань змінюється з часом за законом: A(t) = A₀e^-t

У момент часу t +t: A(t+t) = A₀e^{-(t+ t)}

За умовою задачі: A(t) / A(t+t) = е = (A₀e^-t) / (A₀e^{-(t+ t)}) = e^t Тоді t = 1, тобто  = 1 / t = 0,1 с^-1

6.7. Які значення відповідають частоті власних і вимушених коливань системи, якщо вимушені коливання системи описує рівняння

0,4d²x / dt² + 0,48 dx/dt + 1,6x = 0,8 cos3t

ПРИКЛАД РОЗВ’ЯЗКУ

Диференційне рівняння вимушених коливань має вигляд

d²x / dt² + 2dx/dt + w₀²x = f₀coswt,

де  - коефіцієнт затухань; w₀ - власна частота коливань; w- частота вимушених коливань.

Перепишемо задане рівняння згідно загального вигляду

d²x / dt² + 1,2dx/dt + 4x = 2cos3t,

Тоді частота власних коливань буде

w₀² = 4; w₀ = 2 рад/с

Частота вимушених коливань

W = 3 рад / с

6.8. Яка довжина хвиль, що біжать, якщо зміщення від положення рівноваги точки, яка відстоїть від джерела коливань на відстані х₁ = 4 см у момент t₁= Т/3 дорівнює половині амплітуди?

ПРИКЛАД РОЗВ’ЯЗКУ

Рівняння хвилі має слідуючий вигляд: S(x,t) = Acos(wt – wx / v) = Acos(2t₁/T - 2x₁/) = A/2

Тоді: cos(2t₁/T - 2x₁/) = 1/2

2t₁/T - 2x₁/ =  / 3

Підставимо значення x₁= 0,04 м і t₁= Т/3 та визначимо довжину хвиль, що біжать:  = 2x₁/

6.9. Яка сила F діє на ядра клітин печінки у центрифузі де здійснюється їх сепарація, якщо діаметр клітин d = 8 мкм, густина  = 1,3-10³ кг/м³. Радіус ротора центрифуги R = 0,05 м, частота обертання v = 2 кГц.

ПРИКЛАД РОЗВ’ЯЗКУ

Сила, що діє на об’єм рідини V при центрифугованні з боку рідини, яка оточує,

де ₀ – густина рідини (вода); V = - nd³ - об’єм частинки;

 = 2 - кутова швидкість; R – відстань від частинки до вісі обертання (радіус ротора центрифуги).

З другого боку, доцентрова сила, необхідна для утримання частинки на відстані R від вісі обертання, дорівнює

де ₁ - густина частинки.

Так як ₁ > р₀, то F_l > F_o, тоді частинка рухається від вісі обертання під дією сили

Підставив числові дані, у одиницях СІ (d= 8 • 10^-6 м), отримаємо:

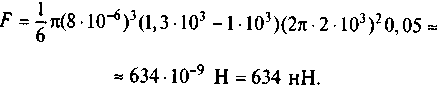
6.10. Яка різниці фаз  у пульсовій хвилі між дво­ма точками артерії, що знаходяться на відстані х = 20 см одна від одної, при цьому швидкість пульсової хвилі дорівнює v = 10 м/с, коливання серця - гармонічні з частотою v = 1,2 Гц.

ПРИКЛАД РОЗВ’ЯЗКУ

Фаза хвилі у точці, яка знаходиться на відстані х в мо­мент часу t

Для точки, що розміщена на відстані (х + х) в тот же момент времени,

Тоді різниця фаз становить:

Подставимо числові дані в одиницях СІ (х - 0,2 м), маємо:

АЛГОРИТМ ВИКОНАННЯ роботи.

7.1. Разом з викладачем студенти обговорюють основні положення теми та розбирають неясні питання. Викладач визначає рівень теоретичної підготовки студентів по питанням, що наведені у п.6.

7.2. Студенти самостійно вирішують задачі і пропоновані викладачем тести.

7.3. Викладач підводить підсумки і дає рекомендації для підготовки до наступного заняття.