Исходные данные

k2:=5 k3:=6 koc:=0.6 t1:=0.005 T1:=0.01

T2:=0.4 T3:=0.04 g:=10 f:=5 G:=8

Коэффициенты характеристического полинома САУ

Kp:=k2 k3 koc

a0:=Kp+1 a1:=T1+T2+T3+Kp t1

a2:=(T2+T3) T1+T2+T3 a3:=T1 T2 T3

Главный минор определителя Гурвица

Так как главный минор определителя Гурвица больше нуля, САУ устойчива.

Определение граничного коэффициента передачи разомкнутой цепи

b1:=T1+T3 b2:=T1 T3

Kgr:=x3(T2) Kgr=155.517

Построение границы устойчивости в плоскости параметров х₁ и х₂

х 1:=0.03, 0.04..0.8

На приведенном графике значения x₁=T₂ и x₂(T₂) показаны посредством маркеров (меток), т.е. установлен флажок в соответствующем пункте графического меню.

Следует отметить, что в некоторых вариантах контрольной работы возможны два решения для границы x₂=(x₁). Они возможны в случае квадратного уравнения вида P(x₁)x₃²+Q(x₁)x₃+R(x₁)=0, где P(x₁), Q(x₁), R(x₁) коэффициенты этого уравнения, зависящие от варьируемого параметра х₁. Если одно решение положительно, а второе – отрицательно, то расчет ведется для границы устойчивости, определенной положительным решением. Если оба решения положительны, то учитывается область устойчивости, ограниченная осями координат и кривой, прилегающей к этим осям, а в качестве граничного значения коэффициента передачи в дальнейших расчетах принимается меньшее из полученных решений.

4. Расчет статических характеристик сау

З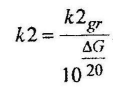 начение коэффициента передачи k₂ для заданного запаса устойчивости по амплитуде G может быть рассчитан по формуле

Внешняя характеристика САУ при изменении возмущающего воздействия от нуля до _m рассчитывается по передаточным функциям замкнутой САУ при p = 0, то есть по формуле

y() = g W_zg(0) -  W_z(0)

Ниже приведена часть расчетного файла , реализующая данный пункт задания в пакете MathCad. Здесь также рассчитано новое значение задающего воздействия g₁, обеспечивающее такое же значение выходной величины, что и в заданной САУ, при  = 0. Легко видеть, что при новом значении к₂ внешняя характеристика САУ более жесткая (то есть при одном и том же значении  наблюдается меньшее отклонение выходной величины от заданного значения). Это подтверждается и меньшим значением статизма.

Расчет статистических характеристик сау

Р ассчет коэффициента передачи к₂, исходя из запаса устойчивости по амплитуде G

Н овое значение коэффициента передачи разомкнутой цепи сау

У точнение задающего воздействия, обеспечивающего одинаковую выходную величину для обеих САУ при  = 0

Уравнение статических внешних характеристик САУ.

Р асчет статистических внешних характеристик

Значение выходной величины при f = 0

Значения выходной величины при f = fm = 10

Отклонения выходной величины от заданного значения при f = fm

С татизм внешних характеристик

5. Расчет логарифмических частотных характеристик сау

А симптотическая ЛАЧХ разомкнутой цепи САУ строится путем суммирования асимптотических ЛАЧХ ее звеньев. В пакете MathCad это осуществляется с помощью условного оператора if. Общая формула для расчета асимптотической ЛАЧХ инерционного, форсирующего и колебательного звеньев имеет вид

Где Т – постоянная времени звена, А – коэффициент наклона ЛАЧХ (- 20, + 20 и – 40 дБ/дек соответственно).

Д ля дифференцирующего и интегрирующего звеньев (при единичном коэффициенте передачи) приведенное выражение будет иметь вид.

Точная ЛАЧХ САУ рассчитывается по формуле

Точная ЛФЧХ рассчитывается как сумма аргументов от АФЧХ звеньев, составляющих САУ, то есть

г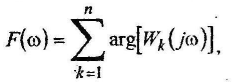 де к – номер звена, n – общее количество звеньев САУ.

Логарифмическая шкала в версиях MathCad для Windows организуется путем включения параметра Log Scale по оси Х графического меню.

Реализация данного пункта задания в пакете MathCad приведена ниже. Частоты среза и переворота фазы находятся с помощью функции Find. Значение фазы -  показано с помощью маркера по оси Y.