Приклади отримання поверхонь відгуку, що геометрично відображають шукані аналітичні значення.

Розрахунок коефіцієнтів регресії багатофакторного поліномінального лінійного рівняння з допомогою методу найменших квадратів.

1. Однофакторне рівняння регресії.

Розглянемо найпростішу одно факторну модель виду

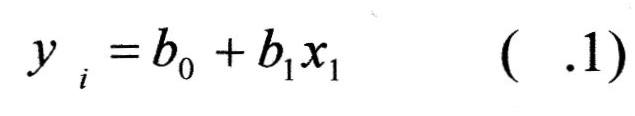
Якщо ця модель адекватна, то для кожного і-того значення справедливими будуть усі рівняння виду

Як видно з вище наведено рівняння, а також графіка, між кожним значенням х_і і у_і існує функціональний зв’язок (лінія 1).

Отже, якщо б не було похибки викликаної через дві причини:

а) похибки самого експерименту (оскільки очевидно, що в жодному випадку будь-який експеримент реалізувати абсолютно точно неможливо),

б) неадекватності самої моделі,

то було б справедливим рівняння ( .2) записати у вигляді:

В реальності ж через вищевказані причини, ліва частина рівняння ( .3) ніколи не дорівнює нулю, а дорівнює певній величині ξ, яка характеризує неспівпадіння експериментальних (лінія 2) та теоретично передбачуваних (лінія 2) даних і називається нев'язкою, а тому має місце рівняння ( .4)

Цілком очевидно, що чим менший модуль величини |ξ|, тим модель є точнішою. Але це твердження відноситься до якоїсь конкретної і-тої точки. Якщо ж спробувати охарактеризувати кількісно точність, з якою наша модель описує експериментальні дані, то зрозуміло, що слід розглядати сумарні відхилення для всіх експериментальних точок. Як було зазначено вище, для цього слід розглядати, або суму модулів нев'язок, або ж суму квадратів нев'язок, що з математичної точки зору є набагато ефективнішим.

Зрозуміло, що чим ця сума менша, тим модель більш точно описує результати експерименту. Величина, яка кількісно характеризує точність з якою та чи інша модель описує результати експерименту, називається адекватністю кожної з моделей. Чисельно адекватність характеризує дисперсія адекватності.

Повернемося до нашої шуканої моделі. Як було зазначено вище, ми будемо прагнути мінімізувати суму квадратів відхилень. Це матиме вигляд:

Ми знаємо, що N - це кількість дослідів в експерименті. Відомо, що мінімум будь-якої функції, якщо він існує, досягається при одночасній рівності нулю часткових похідних по всіх невідомих. Оскільки для кожної і-тої точки значення х_і, та у_і - фіксовані, то зрозуміло, що часткові похідні беруться по коефіцієнтах b₀, b₁, і т.д., тому, що в ще не побудованому рівнянні регресії, саме вони є змінними величинами.

Мінімізувавши суму квадратів відхилень з допомогою розв'язання системи рівнянь виду

ми знайдемо відповідні оптимальні значення коефіцієнтів регресії і в отриманому поліномінальному рівнянні вже коефіцієнти b₀, і b₁ будуть константами, а х та у змінними величинами.

Тепер використаємо умови симетрії матриці планування, звідки отримаємо:

а) умову симетрії вектор-стовпців планування:

б) умову нормування:

Таким чином, добутки та тотожно рівні нулю, а добутки

Отже, ми отримали остаточний розв'зок системи рівнянь, що складається з часткових похідних по шуканих коефіцієнтах регресії від суми квадратів нев'зок всіх дослідів: