§3. Волновая функция и ее физический смысл.

Из содержания предыдущих двух параграфов следует, что с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, поэтому состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени (x,y,z,t). Конкретный вид -функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой – от координат:

(3.1)

В дальнейшем будем рассматривать только стационарные состояния. -функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем , в пределах которого значения -функции будем считать одинаковыми. Тогда вероятность нахождения dW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля -функции (квадрата модуля амплитуды волн де Бройля): (3.2)

Отсюда следует физический смысл волновой функции: . (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля: (3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объему V, должен быть равен единице: (3.5)

– условие нормировки -функции.

Чтобы волновая функция являлась объективной характеристикой со­стояния микрочастиц, она должна быть конечной, однозначной, непре­рывной, так как вероятность не может быть больше единицы, не может быть неоднозначной величиной и не может изменяться скачками. Таким образом, состояние микрочастицы полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля.

§4. Уравнение Шредингера. Электрон в потенциальной яме.

Как, зная структуру силового поля, в котором движется частица, определить волновую функцию, описывающую квантовомеханическое состояние этой частицы? Как, зная волновую функцию в начальный момент времени, описать эволюцию волновой функции во времени? Ответы на эти вопросы дает основное уравнение нерелятивистской квантовой механики, сформулированное Э.Шредингером в 1926 г.

Основной характеристикой состояния атомов, молекул, элементарных частиц является -функция. Аналитическое выражение -функции в каждом конкретном случае можно получить путем решения волнового уравнения – основного урав­нения квантовой механики, предложенного Э. Шредингерам в 1920 г.

Применительно к стационарным состояниям уравнение Шредингера имеет вид:

. (4.1)

где т – масса частицы; Е и U – ее полная и потенциальная энергии.

Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шрёдингера упрощается и принимает вид:

(4.2)

Одним из наиболее простых примеров использования уравнения Шрёдингера является решение задачи о движении частицы в одномерной потенциальной яме.

Пусть электрон перемещается вдоль оси ОХ только в пределах 0<х<l (рис. 4.1). Это означает, что в указанном интервале -функция отлична от нуля, а вне интервала (х < 0, х l) равна нулю:

(0<х<l)  0 (х0) = 0 ( х l) = 0

Т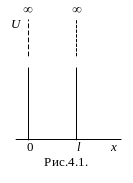 ак как на частицу в выделенном интервале силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять U=0). Вне этого интервала электрона нет, поэтому следует считать его потенциальную энергию бесконечно большой. На рис. 4.1 показана графическая зависимость U = f(x).

     

Интервал 0<х<l, удовлетворяющий сформулиро­ванным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом U=0 уравнение Шрёдингера (4.2) для интервала 0<х<l имеет вид:

. (4.3)

Введем обозначение: , (4.4)

тогда: (4.5)

Это уравнение аналогично дифференциальному уравнению гармонического колебания, решение которого: , (4.6)

где –амплитуда волновой функции, –ее начальная фаза. Чтобы найти две постоянные и , а также возможные значения или Е, рассмотрим граничные условия:

1) при х =0  = 0. Подставляя эти значения в (4.10), получаем

Физический смысл здесь имеет только одно значение: , откуда .

2) при х =l  = 0. C учетом из (4.10) имеем:

Физический смысл здесь имеет только одно значение:

, или , откуда

, (4.7)

где п – целое число, оно принимает значения 1, 2, 3, ...; п ≠ 0, так как в противном случае = 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число n называют квантовым числом. Из (4.4) находим энергию , что с учетом (4.7) дает:

. (4.8)

Индекс n при Е показывает, что различным значениям квантового числа n соответствует и разная энергия.

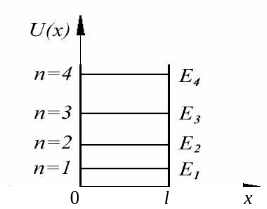
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.

Состояние частицы с наименьшей энергией, в данном случае с , называется основным состоянием. Все остальные состояния являются возбужденными: значение отвечает первому возбужденному состоянию, значение - второму возбужденному состоянию и т.д.

Подставляя  (4.7) в (4.5) и учитывая , получаем

. (4.9)

     Таким образом, для получаем

     

Из (4.8) следует, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии: ; и т.д.

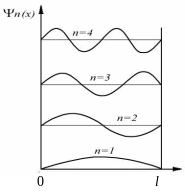
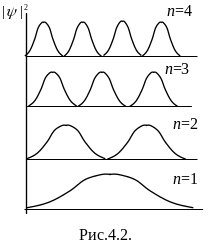
Возведя (4.9) в квадрат, получим плотность вероятности нахождения электрона в разных точках потенциальной ямы. На рис.4.2. показана графическая зависимость от х при разных дискретных состояниях, то есть разных квантовых числах. Как видно из рисунка, электрон может с разной с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в которых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым равновероятно нахождение частицы в раз­ных местах потенциальной ямы

Плотность вероятности оказывается существенно различной для разных состояний частицы, т.е. для разных значений квантового числа . Так, например, в основном состоянии, т.е. при , частица с наибольшей вероятностью находится в центре ямы, а в первом возбужденном состоянии, т.е. при , вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно. Такое поведение кардинально отличается от поведения в яме классической частицы, для которой плотность вероятности нахождения частицы одинакова в любой точке ямы.