Конспект по эконометрике на тему “Стационарные процессы” стр 10 из 10

Стационарные стохастические процессы.

Набор случайных переменных Х(t) называется стохастическим процессом.

Дискретный стохастический процесс определяется как последовательность случайных переменных Х(t), где t=t₁, t₂, …,t_Т или Х_t.

Параметры стохастического процесса:

М[Х_t]=μ_t- представляет собой функцию времени;

²[Х_t]=M[(Х_t-μ_t)²] - представляет собой также функцию времени;

Автоковариация γ_t1,t2=cov[Х_t1,Х_t2]=M[(Х_t1-μ_t1)∙( Х_t2-μ_t2)]- зависит от каждого сочетания t1 и t2.

Конечная реализация х₁, х₂, ..., х_Т дискретного стохастического процесса Х₁ , Х₂ , ...,Х_Т называется временным рядом (или сгенерированным стохастическим процессом).

Стохастический процесс стационарен в сильном смысле слова, если совместное распределение вероятностей всех переменных Х_t1 , Х_t2 , ...,Х_tn точно такое же, что и для переменных Х_t1+τ , Х_t2+τ , ...,Х_tn+τ.

Под стационарным процессом в слабом смысле, понимается процесс, для которого среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянные значения, а автоковариация зависит только от τ, т.е.:

μ_t=μ= const;

²_t=² =const;

γ_t1,t2= γ_t+τ,t= γ_τ, где τ- лаг (t₁=t+τ, t₂=t);

(γ₀= М[(Х_t1-μ_t)∙( Х_t1-μ_t)]=М[(Х_t2-μ_t)∙( Х_t2-μ_t)]=... =М[(Х_tn-μ_t)∙( Х_tn-μ_t)]=²_t=²).

r[X_t+τ ,X_t]=r_τ = γ_τ/ γ₀ - коэффициент автокорреляции.

Упорядоченные по τ значения ρ_τ представляют автокорреляционную функцию. Графическое представление зависимости ρ_τ от τ называют коррелограммой.

На практике стационарность временного ряда означает:

- отсутствие тренда;

- отсутствие систематических изменений дисперсии;

- отсутствие строго периодических флуктуаций;

- отсутствие систематически повторяющихся взаимодействий между элементами.

Реальные экономические ряды (например, ВВП, ...) являются, как правило, нестационарными.

Подходы к распознаванию временных рядов:

1. графический метод (по линейной диаграмме);

2. исследование на наличие автокорреляции в реальных данных;

3. тесты на присутствие детерминистского тренда;

4. тесты на наличие стохастического тренда, например, тесты на единичный корень.

Особые случае стационарных стохастических процессов.

«Белый шум» - чисто случайный процесс ,т.е. ряд независимых величин _t. Главные свойства «белого шума»:

μ[_t]=μ= const;

²[_t]=²_ =const;

γ_t1,t2= γ_τ=0 (для t₁t₂);

Проверить, является ли временной ряд «белым шумом» можно при помощи теста Бокса-Пирса.

Основная гипотеза Н0: процесс является «белым шумом».

Статистика критерия проверки гипотезы:

Q=T имеет ² распределение с числом степеней свободы равным р.

Если Q<²_(;р), то гипотеза Н0 не отвергается.

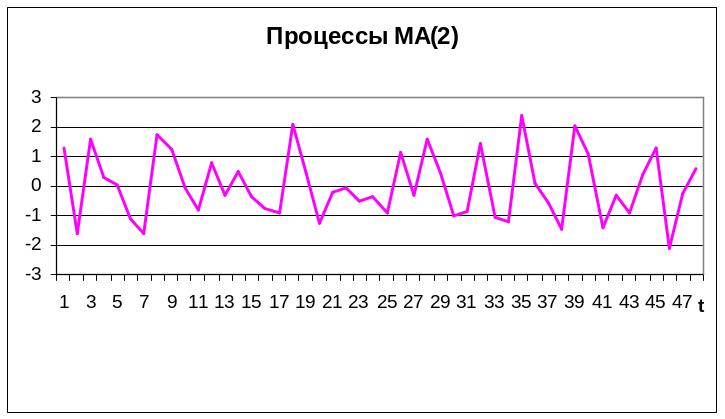
Модель МА(q) – скользящего среднего:

Х_t=_t - ₁∙_t-1- ₂∙_t-2- …-_q∙_t-q, где _t – «белый шум» с μ_=0.

Тогда:

М[Х_t]=0;

²[Х_t]=²_ + ²[-₁∙_t-1]+ ²[-₂∙_t-2]+…+ ²[-_q∙_t-q] =

=²_ + ₁∙²_+ ₂∙²_+…+ _q∙²_ = ²_ =²_(1+²₁+²₂+...+²_q);

γ_t+τ,t= γ_τ =M[(_t+τ - ₁∙_t+τ-1- ₂∙_t+τ-2- …-_q∙_t+τ-q)∙( _t - ₁∙_t-1- ₂∙_t-2- …-_q∙_t-q)] =

=²_(-_τ+₁∙_τ+1+₂∙_τ+2+…+_q-τ∙_q)=²_ ;

Например при τ=2, q=4.

Х_t=_t - ₁∙_t-1- ₂∙_t-2-₃∙_t-3-₄∙_t-4 :

γ_t+2,t= γ₂ =

=M[(_t+2 - ₁∙_t+2-1 - ₂∙_t+2-2 - ₃∙_t+2-3-_q∙_t+2-4)∙( _t - ₁∙_t-1- ₂∙_t-2 -₃∙_t-3-_q∙_t-4)] =

=M[-₂∙²_t+₃∙₁∙²_t-1+₃∙₁∙²_t-1+₂∙₄∙²_t-2]= M[²](-₂+₃∙₁+₂∙₄).

(M[_ti,_tj]=0 для всех t_it_j)

r[X_t+τ ,X_t]=r_τ= γ_τ/ γ₀ = (-_τ+₁∙_τ+1+₂∙_τ+2+…+_q-τ∙_q)/ (1+²₁+²₂+...+²_q).

Модель АR(p) – авторегрессии:

Х_t= [₀]+₁∙Х_t-1+ ₂∙Х_t-2+ …+_р∙Х_t-р+ _t, где _t – «белый шум» с μ_=0.

Авторегрессионный процесс AR(q) можно свести к процессу скользящего среднего MA(). То есть имеет место обратимость процессов.

Например AR(1)-процесс:

X_t= ₁∙X_t-1+ _t= ₁∙(₁∙X_t-2+ _t-1)+ _t= ₁²∙X_t-2+₁∙_t-1+_t= ₁²∙(₁∙X_t-3+ _t-2)+₁∙_t-1+_t=

= ₁³∙X_t-3+₁²∙_t-2+₁∙_t-1+_t =... = .

Тогда:

М[Х_t]=[₀]+0;

²[Х_t]=²_ (1+₁+₁²+₁³+...) = (если ₁ <1);

γ_t+τ,t= γ_τ =²[X_t]∙₁^τ ;

r[X_t+τ ,X_t]=r_τ= γ_τ/ γ₀ = .

Процесс авторегрессии не всегда стационарен. Процесс будет стационарным только в том случае, если все корни характеристического уравнения:

1-₁∙z- ₂∙z²- ₃∙z³- …-_р∙z^p=0 лежат вне единичного круга (т.е. │z│>1).

Если же │z│1, процесс нестационарен.

Если же │z│=1, процесс называется процессом единичного корня.

В случае AR(1): Х_t= [₀]+₁∙Х_t-1+ _t нестационарным процесс будет, если корни характеристического уравнения: 1-₁∙z =0 меньше или равны единице.

То есть │z│= . Тогда условие стационарности будет:│₁│<1.

Если │z│=│₁│=1, то имеем процесс единичного корня: Х_t=Х_t-1+ _t .

Условие стационарности для модели авторегресии 2-ого порядка - AR(2):

Х_t= [₀]+₁∙Х_t-1+ ₂∙Х_t-2+ _t (процессов Юла)/

Решая характеристическое уравнение: 1-₁∙z- ₂∙z²=0 относительно z получаем:

z=f(₁,₂)│>1. Отсюда:

Так как процессы авторегрессии и скользящего среднего обратимы, то имеется условие обратимости и для процессов скользящего среднего:

все корни характеристического уравнения: 1- ₁∙z - ₂∙z² - ₃∙z³ - _q∙z^q =0 должны лежать вне единичного круга: │z_j│>1 для всех j=1;q.

Тогда для МА(1): из характеристического уравнения: 1- ₁∙z =0 получаем условие обратимости:│₁│<1.

Для МА(2) из характеристического уравнения: 1- ₁∙z - ₂∙z² =0 получаем условие обратимости:

.

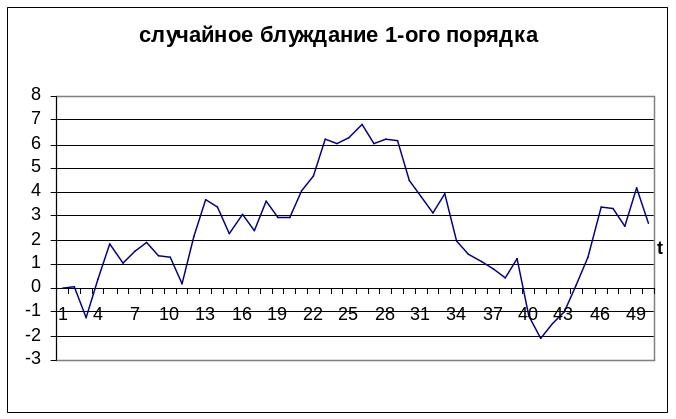
Процессы единичного корня:

Х_t=Х_t-1+ _t - случайное блуждание.

Данный процесс является нестационарным, т.к. корень характеристического уравнения: z -1=0 (а это z=1) лежит в точности на единичном круге.

Модели авторегрессии и скользящего среднего ARMA(p,q):

Х_t= [₀]+₁∙Х_t-1+ ₂∙Х_t-2+ …+_р∙Х_t-р+ _t - ₁∙_t-1- ₂∙_t-2- …-_q∙_t-q или

Х_t- [₀]-₁∙Х_t-1- ₂∙Х_t-2- …-_р∙Х_t-р = _t - ₁∙_t-1- ₂∙_t-2- …-_q∙_t-q.

При общих условиях стационарный ARMA – процесс может быть представлен как бесконечный AR или MA процесс.