Ответы на экзаменационные вопросы по физике / 20

3

2. Атом водорода

Э

лектрон в атоме водорода движется в силовом поле положительно заряженного ядра, т. е. находится в потенциальной яме с рельефом вида: U = - kq_е²/r.

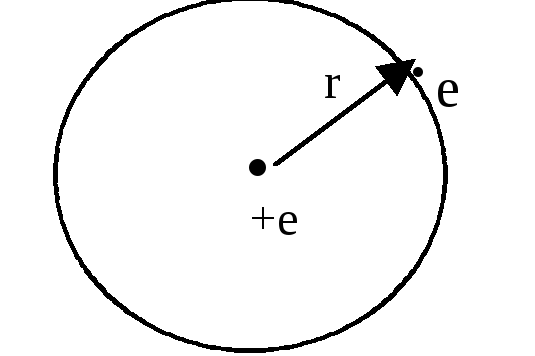
Граничные условия имеют характер: .

Таким образом, имеем потенциальную яму бесконечной глубины (ящик) с радиальной симметрией, со стенками гиперболической формы (фигура вращения - типа грамофонной трубы).

Кинетическая энергия электрона Т = kq_е²/2r и полная энергия Е = Т + U = - kq_е²/2r = - T = |U|/2.

В соответствии с изложенными выше соображениями, можно сразу сделать заключение о бесконечно большом числе уровней энергии электрона в атоме водорода. Энергия электрона остается дискретной до тех пор, пока ее значение остается отрицательным; этому соответствует связанное состояние электрона в атоме, электрон остается внутри ямы.

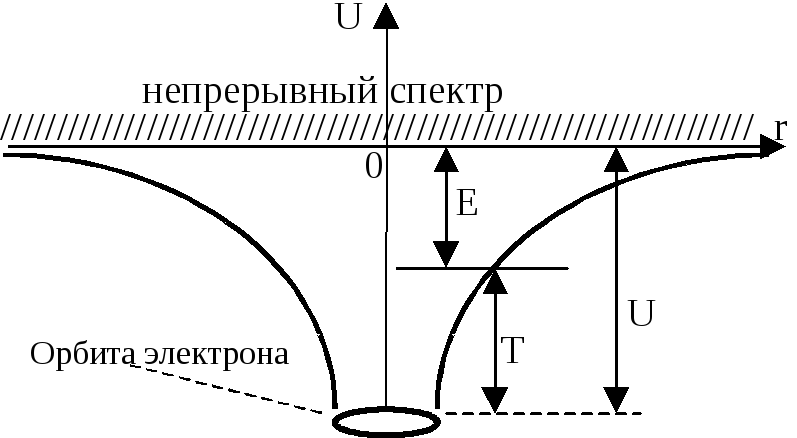
Электрон за счет туннельного эффекта может кратковременно выйти за пределы ямы, (за границы), но затем обязан вернуться в нее обратно. Поэтому в квантовой теории говорят, что электрон вращается не по орбитам, а как бы размазан в пространстве в виде облака вероятности его различных местонахождений.

Стационарное уравнение Шредингера для электрона в атоме водорода имеет вид:

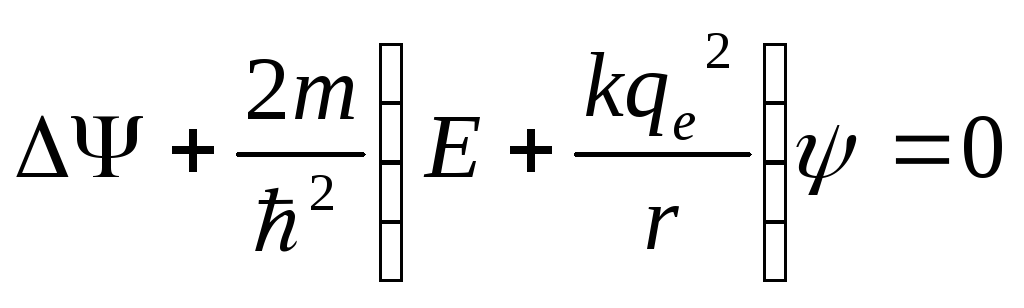
В силу наличия сферической симметрии потенциальной энергии, уравнение Шредингера целесообразно записать и решать в сферической системе координат r, , . Оператор Лапласа  в сферических координатах запишется так:

 = ² /x² + ² /y² + ² /z² = 1/r² /r(r² /r) + (1/r²sin ) /(sin  /) + (1/r²sin² )² /²

И уравнение Шредингера:

[1/r² /r(r² /r) + (1/r²sin ) /(sin  /) + (1/r²sin² )²/²] + (2m/²)(Е + kq_е²/r) = 0

Представляем  - функцию в виде произведения трех сомножителей с разделенными переменными r, , : ( r, , ) = R(r)  ()  Ф(). Решаем уравнение Шредингера методом разделения переменных. Возможность такого разделения доказывается в процессе решения.

После подстановки выражений для потенциальной энергии и волновой функции  электрона в атоме водорода в уравнение Шредингера, оно распадается на три уравнения, каждое из которых записано для своей сферической координаты:

1) R(r) = ₁(n, l); 2) () = ₂(l, m); 3) Ф() = ₃(m).

В этих уравнениях появляются квантовые числа n, l, m, как параметры при решениях соответствующих уравнений.

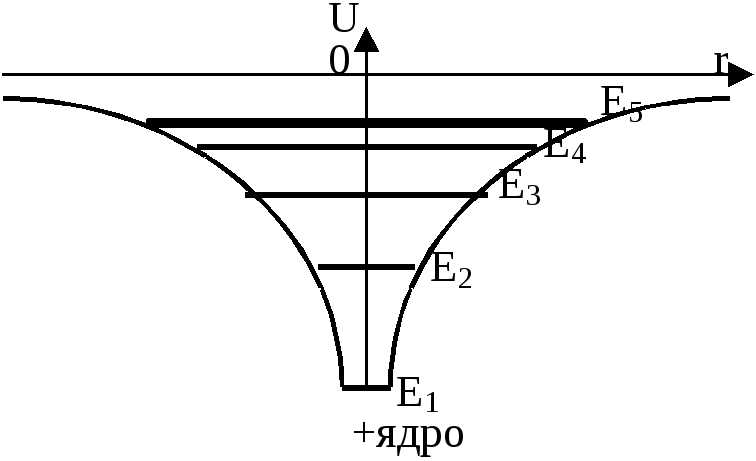
Решив три уравнения, получаем выражение для полной энергии электрона в атоме водорода, которая квантуется: Е_n = - k²mq_е⁴/2n²². Это выражение совпадает с полученным ранее в полуклассической теории Бора. Напомним, что Бор, и позднее Зоммерфельд, постулировали введение квантовых чисел в теорию. Здесь же, в квантовой теории, квантовые числа вводятся не "вручную", а вытекают естественным образом в результате решения уравнения Шредингера. Четвертое квантовое число – спиновое, в нерелятивистском уравнении Шредингера не появляется. Оно вытекает из более общего, релятивистского уравнения Дирака.

Главное квантовое число n и в квантовой, и в классической теории определяет полную энергию электрона в атоме водорода: Е_n = - k²mq_е⁴/2n²².

Орбитальное (азимутальное, побочное) квантовое число l, по Бору-Зоммерфельду, определяло форму орбиты электрона (ее отличие от круговой орбиты, ее "эллиптичность"). В квантовой же теории это число определяет форму электронного облака и численно - момент импульса электрона в нем:

.

Число l = 0, 1, 2, … (n - 1) изменяется, начиная с нуля, а у Бора с 1. При l = 0, L = 0 - нет вращения. Электронное облако имеет конфигурацию сферы. Такое состояние, называемое S - состоянием, в классической теории невозможно. Там орбиты были плоскими, и сферически симметричный случай был невозможен. Состоянию с нулевым значением момента импульса в теории Бора соответствовало бы прямолинейное движение электрона вдоль диаметра атома.

Магнитное квантовое число m у Бора - Зоммерфельда определяло ориентацию эллиптической орбиты электрона в пространстве, а в квантовой теории - ориентацию электронного облака в пространстве и численно - проекцию L_ момента импульса на некоторое выделенное направление z:

L_z = m, где m = 0,  1,  2, …  l.

Для l = 0 (S - состояние) и m = 0 - сферическая симметрия, нет никакой избранной симметрии в пространстве, то есть каких-либо выделенных в нем направлений.

Рассмотрим поподробнее 1S - состояние – простейший, сферически симметричный случай распределения плотности вероятности в пространстве. Это состояние является стационарным невозбужденным. В нем волновая функция (r, , ) = (r) - не содержит зависимости от угловых координат  и , и уравнение Шредингера запишется так:

.

Решение ищем в виде - простейшей сферически симметричной функции. Подставив в уравнение Шредингера, получим:

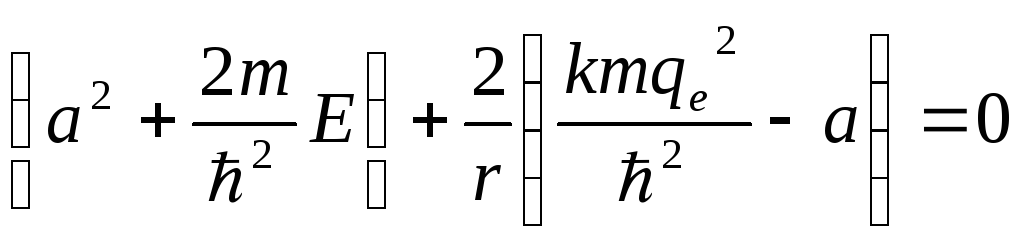
Полагаем равными нулю каждое из слагаемых по отдельности:

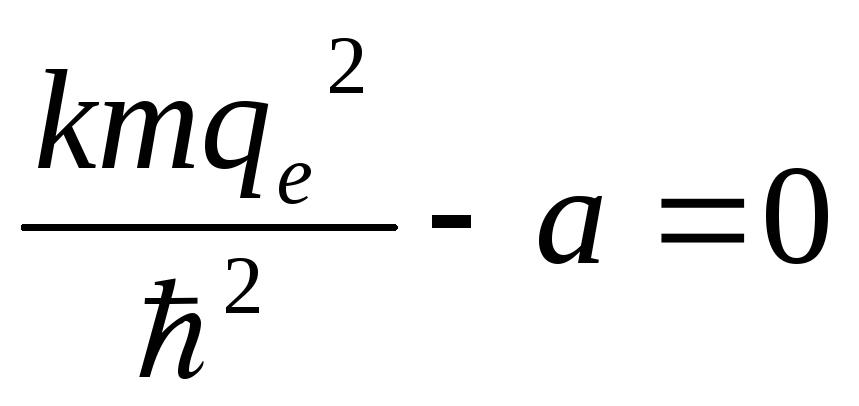и ; и .

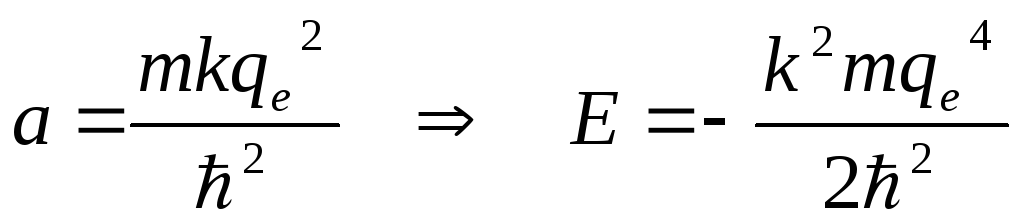В итоге для энергии электрона в 1S - состоянии имеем: 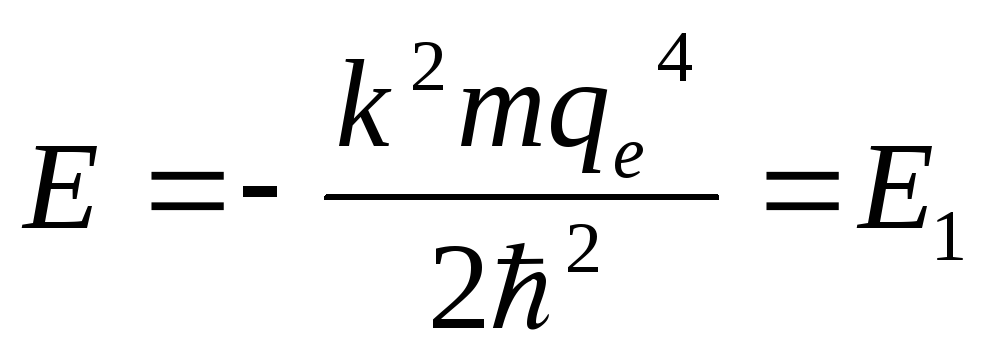- как у Бора.

В

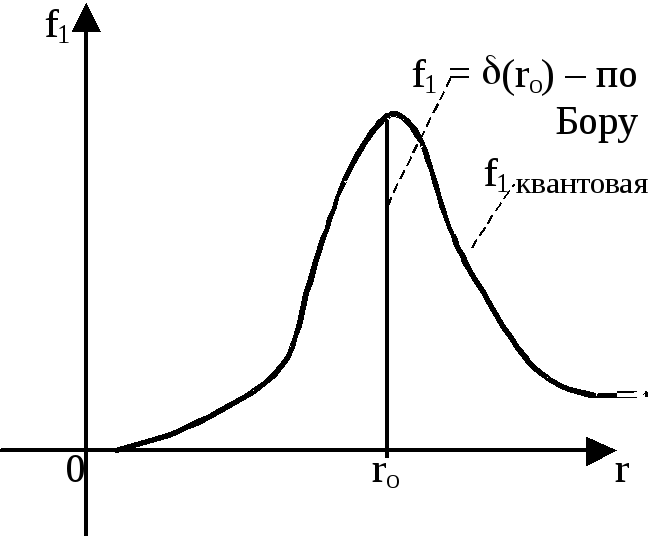
ероятность dP₁ местонахождения электрона в элементарном сферическом (шаровом) слое с объемом dV = 4r²dr равна: . Радиальная плотность вероятности (радиальная функция распределения): - функция с максимумом. Плотность вероятности имеет максимум, при r = r_о, который и соответствует значению радиуса первой орбиты по теории Бора.

. У Бора для радиуса орбит было: .

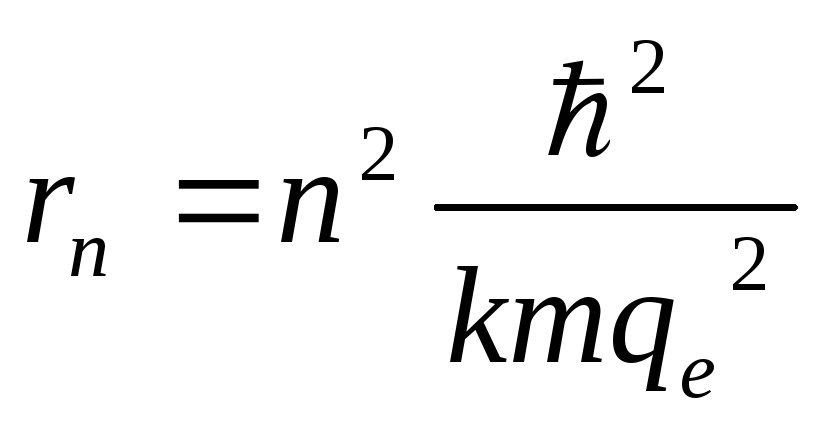По теории Бора - Зоммерфельда электроны в атоме вращались по орбитам. В квантовой механике орбит как таковых нет, а есть целые пространственные области (облака), в которых электрон может находиться с разной вероятностью. Но у этого облака пространственного распределения вероятности местонахождения электрона есть максимумы, которые и попадают на радиусы боровских орбит. Таким образом, теория Бора есть некоторое приближение к более глубокой и полной, адекватной теории микробытия - к квантовой теории.

В невозбужденном 1S - состоянии вероятность найти электрон в разных направлениях одна и та же, зависящая только от радиуса. В возбужденных состояниях (при n  1 и l  0) плотность вероятности начинает зависеть и от углов  и . Рассмотрим, например, состояние с

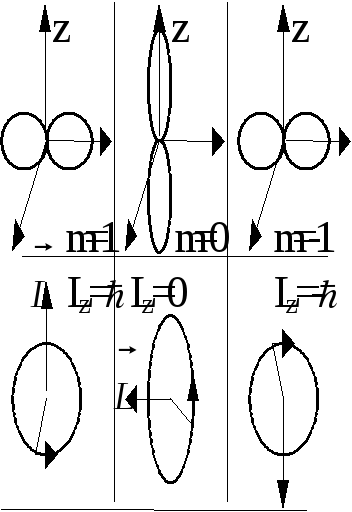
= 1, называемое р - состоянием. В нем имеем три ориентации облака вероятности с m = 0,  1.

Для l = 1 она изображается фигурой типа гантели. Вдоль направления вероятность найти электрон по теории Бора, равна нулю.

Д

ля l = 2; d - состояние: m = 0,  1,  2 - итого пять ориентаций; две взаимно перпендикулярных гантели.

Для электрона в атоме водорода, как и для гармонического осциллятора, существуют определенные правила отбора, ограничивающие число возможных переходов электрона в атоме, связанных с дипольным излучением и поглощением света. Согласно этим правилам, побочное квантовое число l может изменяться на единицу, то есть l =  1, а магнитное квантовое число m – на ноль и единицу, то есть m = 0,  1. Переходы электрона с n – го на первый уровень (серия Лаймана), то есть в 1S состояние, могут осуществлять лишь из р – состояний: nр  1S. Соответственно переходы электрона на второй уровень (серия Бальмера) могут происходить по схемам: nр  2S, nS  2р, nd  2р.