Ответы на экзаменационные вопросы по физике / 19

Влияние формы потенциальной ямы на квантование энергии частицы

1. Гармонический осциллятор.

П

од гармоническим (линейным) осциллятором понимают частицу (систему), на которую действует упругая сила F = - kx, и под действием которой частица совершает гармонические колебания. Потенциальная энергия при этом определяется формулой U = kх²/2. Такой потенциальный профиль представляет собой потенциальную яму (ящик) со стенками параболической формы.

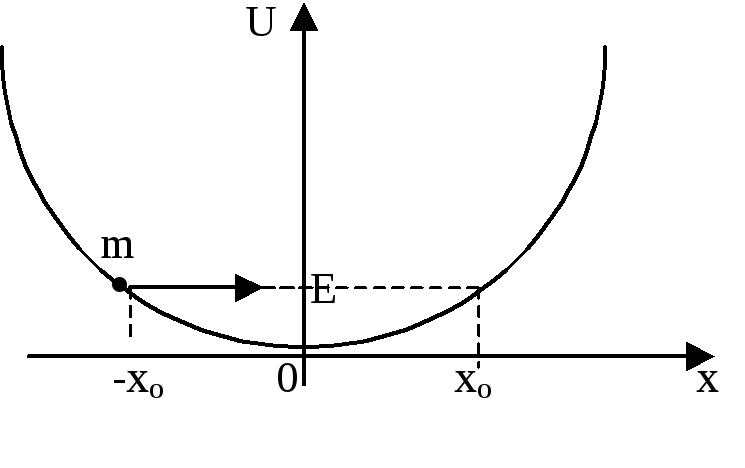
В соответствии с рассмотренными ранее общими условиями, энергия линейного гармонического осциллятора должна квантоваться, т. е. принимать дискретные значения.

Напомним сначала результаты классического рассмотрения задачи о гармоническом осцилляторе. Там, на основе уравнения движения - второго закона Ньютона: с упругой силой F = - kx, получается решение в виде: , где - частота собственных колебаний осциллятора. Потенциальная энергия и кинетическая энергия осциллятора изменяются так, что их сумма . Таким образом, в классическом случае амплитуда и энергия колебаний изменяются непрерывно, будучи ограничены пределами, соответственно, x_о и . 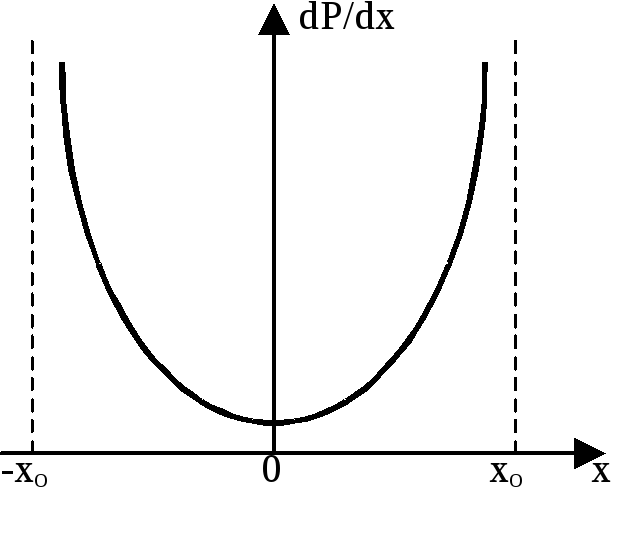Качественно можно оценить распределение вероятностей местонахождения гармонически колеблющейся частицы. Положение равновесия х = 0, осциллятор пролетает, имея наибольшую скорость, т. е. наиболее быстро. На краях же (в точках поворота), при х =  х_о, осциллятор (маятник) замедляется до нулевой скорости. При этом притормаживании он задерживается в крайних точках, проводя в них время заметно большее, нежели в положении равновесия при х = 0. Таким образом, это качественное рассмотрение позволяет сделать вывод о том, что плотность вероятности dР/dх местонахождения осциллятора в положении равновесия минимальна, а в крайних точках - максимальна.

К

вантовый подход к анализу движения осциллятора.

Уравнением движения берем уравнение Шредингера для стационарных состояний

с потенциальной энергией в виде: , где k = m_о².

Подставляя в уравнение Шредингера выражение для U, имеем:

.

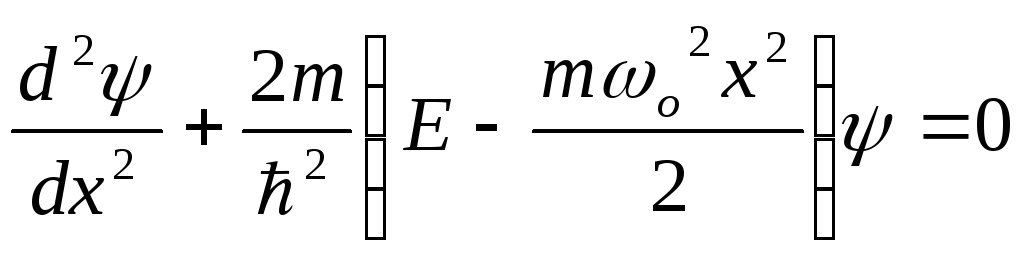Как показывается в теории дифференциальных уравнений, решение уравнения для линейного гармонического осциллятора имеет место лишь при определенных значениях энергии Е, которая играет роль параметра в уравнении. Разрешенные значения энергии линейного гармонического осциллятора, называемые его собственными значениями, выражаются следующей формулой:

Е_n = (n + 1/2)_о, где n = 0, 1, 2, ...

Энергетический спектр гармонического осциллятора является эквидистантным с = const.

В отличие от атома водорода, спектр гармонического осциллятора содержит всего одну спектральную линию, соответствующую частоте _о. Поэтому осциллятор может совершать переходы с n – го уровня лишь на соседние (n  1) - ые уровни. Эта его особенность отражается в существовании специального правила отбора для квантового числа n =  1. В соответствии с ним, квантовое число n гармонического осциллятора единовременно может изменяться лишь на единицу.

При n = 0 имеем состояние с так называемой нулевой энергией Е_о = _о/2. Наличие нулевой энергии является характерным отличием квантовой теории, специфическим квантовым эффектом. Его необходимость проистекает уже из соотношений неопределенности Гейзенберга, ибо Е_о = 0 означало бы наличие одновременно точных значений (нулевых) и координаты, и импульса.

В

классической теории наименьшая энергия осциллятора определялась температурой в соответствии с выражением E = kT = 0. Классическая теория допускала абсолютный покой. У квантового осциллятора существует наименьшая (нулевая) энергия, которую нельзя отобрать никаким охлаждением: Е_о = /2. Плотность вероятности местонахождения классической частицы в этом состоянии выражается так называемой дельта - функцией:

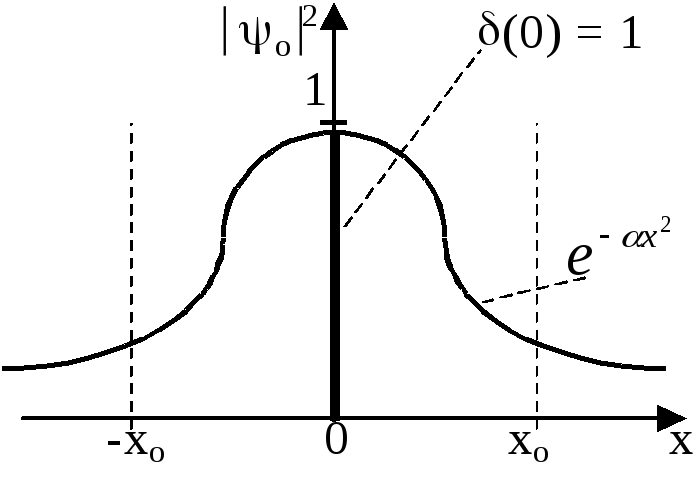
Квантовомеханический анализ приводит к следующему выражению для плотности вероятности в самом нижнем (нулевом) состоянии (при n = 0) .

Эта зависимость изображается так называемой Гауссовой кривой (или гауссианой).

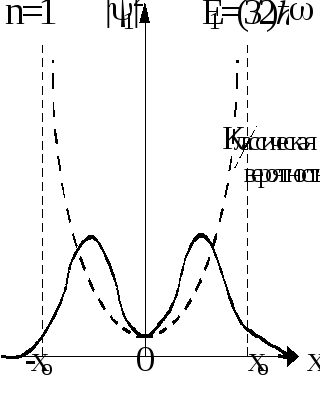
Соответственно в следующих, возбужденных состояниях с n = 1, 2, ... плотность вероятности имеет следующий вид:

С возрастанием n волновая функция осциллирует все чаще, соответственно, возрастает число «равновероятных» мест, которые при n   покрывают собой практически всю доступную осциллятору область. Все меняется столь часто, что практически ничего не меняется. Имеем, согласно принципу соответствия, переход к классической механике.

Микрочастица может за счет туннелирования с некоторой вероятностью выходить за пределы  x_о, куда макрочастица заходить не может. Но всегда микрочастица возвращается обратно, ибо она связана, являясь осциллятором (гармонически колеблющейся системой