Контрольные вопросы:

1. Какие системы уравнений можно решать методом Гаусса?

2. В чем заключается прямой и обратный ход метода Гаусса?

3. Для чего еще можно использовать прямой ход метода Гаусса?

4. Как избежать деления на ноль при решении системы уравнений методом Гаусса?

5. Какие преимущества и недостатки можно выделить при решении системы уравнений методом Гаусса, используя Microsoft Excel?

Пример выполнения задания

Решить:

3,88 3,78 3,45 10,41

3,00 2,79 2,39 8,36

2,67 2,37 1,96 7,62

Воспользовавшись формулами 1 и 2 необходимо выбрать ведущий элемент и выполнить четыре шага.

шаг_0
3,88	3,78	3,45	10,41
3	2,79	2,39	8,36
2,67	2,37	1,96	7,62
шаг_1
1	0,974227	0,889175	2,68299		1	0,974227	0,889175	2,68299
0	-0,13268	-0,27753	0,311031		0	-0,23119	-0,4141	0,456418
0	-0,23119	-0,4141	0,456418		0	-0,13268	-0,27753	0,311031
шаг_3
1	0,974227	0,889175	2,68299
0	1	1,791193	-1,97425
0	0	-0,03987	0,049087
шаг_4
1	0,974227	0,889175	2,68299
0	1	1,791193	-1,97425
0	0	1	-1,23119

Воспользовавшись формулой 3 необходимо выполнить обратный ход метода Гаусса и сделать проверку.

x3	-1,23119		проверка	10,41
x2	0,231049			8,36
x1	3,552638			7,62

Пример решения в Mathcad:

Приближенное решение уравнения методом деления пополам (метод бисекций)

Методические указания

Пусть задана непрерывная функция , и требуется найти корни уравнения . Локализация корней заключается в определении отрезка [A, B], на котором функция принимает значения разных знаков, т.е. . Тогда по теореме Больцано-Коши внутри отрезка существует такая точка С, что . Определение числа корней функции и выделение содержащих их отрезков осуществляется с помощью исследования графика функции.

Пусть отрезок [A, B] определен. Итерационный метод бисекций состоит в построении вложенных последовательности отрезков , на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти корень функции с любой заданной точностью.

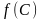Опишем один шаг итераций. Пусть на (п-1)-м шаге найден отрезок такой, что . Разделим его пополам точкой и вычислим значение . Если , то С – корень уравнения. Если , то из двух половин отрезка выберем ту, на концах которой функция принимает разные знаки, т.к. корень находится в этой половине.

, если , (5)

, если . (6)

Если точность нахождения корня  задана, то итерационный процесс продолжается до тех пор, пока длина отрезка станет не меньше 2. Тогда координата середины отрезка и есть значение корня с требуемой точностью.

Метод бисекций – надежный способ отыскания простых корней функции. Он сходится для любых непрерывных, в том числе и недифференцируемых функций, однако скорость сходимости невелика. Для достижения заданной точности  необходимо совершить N итераций, где

. (7)

Метод неприменим для отыскания кратных корней четного порядка. В случае отыскания корней нечетной кратности он менее точен.