4.7 Определение масс небесных тел

Из механики известно, что для точки, равномерно движущейся по кругу, центростремительное ускорение а_ц = ²R , где  — угловая скорость точки, равная =2/Т (Т  период обращения), а R — радиус круга. Принимая орбиту Луны за окружность с приближенным радиусом R = 384000 км, а период обращения Луны вокруг Земли равным примерно 27,3 средних суток (сидерический месяц), получим центростремительное ускорение орбитального движения Луны

.

Эта значение совпадает с величиной, полученной в разделе (4.6.1) по формулам, вытекающим из закона всемирного тяготения. Для Земли, движущейся вокруг Солнца получим, что её центростремительное ускорение равно а_ц=0,59 см/сек² такое же значение получим из (4.20).

Приравняем центростремительное ускорение какого либо тела к ускорению силы притяжения от другого тела (4.20), движущимся по орбитам вокруг друг друга

. (4.27)

Такое же выражение можно записать и для второго тела

. (4.28)

Складывая уравнения (4.27) и (4.28), получим

, где r₁+r₂=r (4.29)

Преобразуем выражение (4.29)

. (4.30)

Это выражение справедливо для любых пар тел, например для планеты, обращающейся вокруг Солнца, или для спутника, обращающегося вокруг планеты. Следовательно выражение (4.30) можно записать для систем Солнце  Земля и для Земля  Луна:

, (4.31)

, (4.32)

где М_С  масса Солнца, m_  масса Земли, m_  масса Луны, Т_  период обращения Земли вокруг Солнца, Т_Л  период обращения Луны вокруг Земли, r_  астрономическая единица, а r_Л  расстояние от Земли до Луны. Разделив уравнение (4.31) на уравнение (4.32), получим

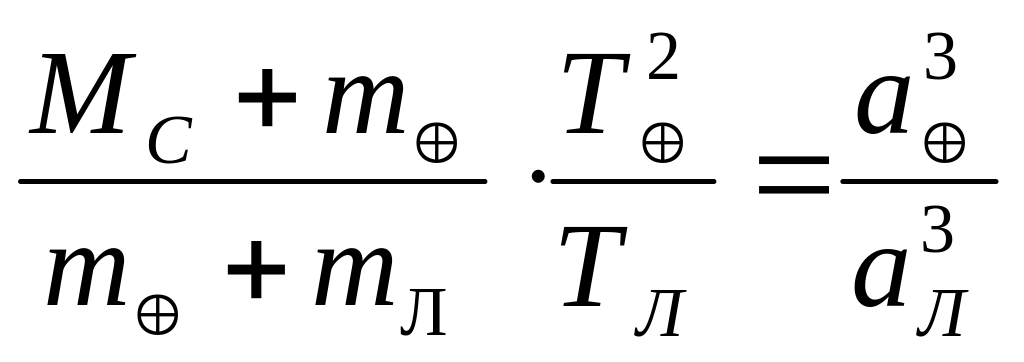. (4.33)

Из (4.33), зная массу Земли можно найти массу Солнца. Из закона всемирного тяготения для Земли

g=ƒm_/R²_{; (4.34)}

m_=g·_R²/ƒ (4.35)

По известным g, R и ƒ масса Земли будет

m_=5,97610²⁷г≈610²⁷г·, а средняя плотность ≈5,52 г/_см³ _.

Учитывая, что m_ многократно меньше М_С (в 333 000 раз), а m_Л меньше m_ в 81,3 раза , то выражение (4.33) можно переписать как:

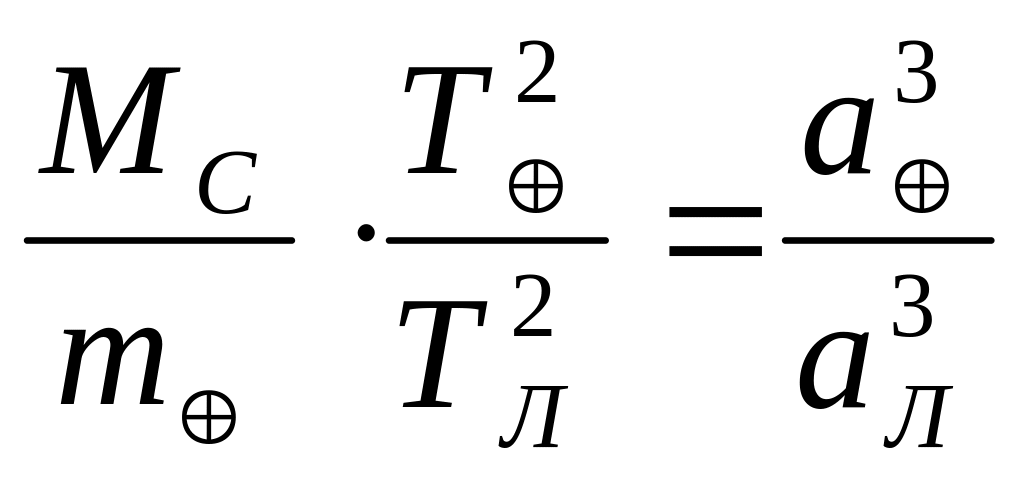, (4.36)

Отсюда М_С можно найти из выражения

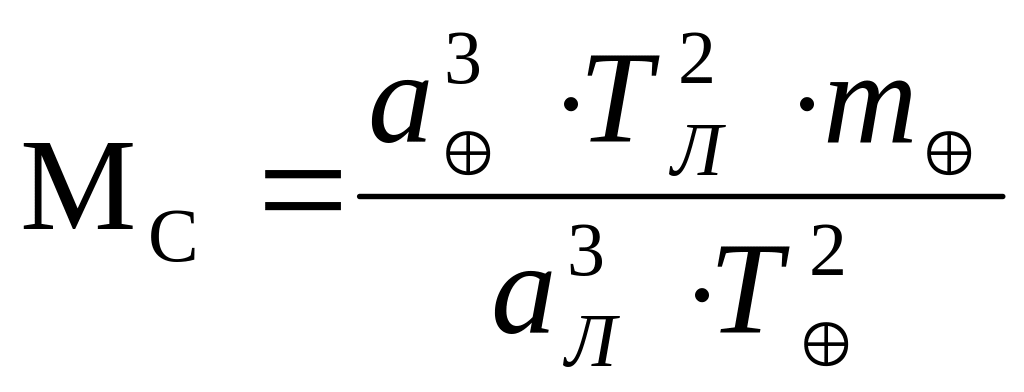. (4.37)

Для любых двух пар притягивающих тел выражение (4.33) можно записать как

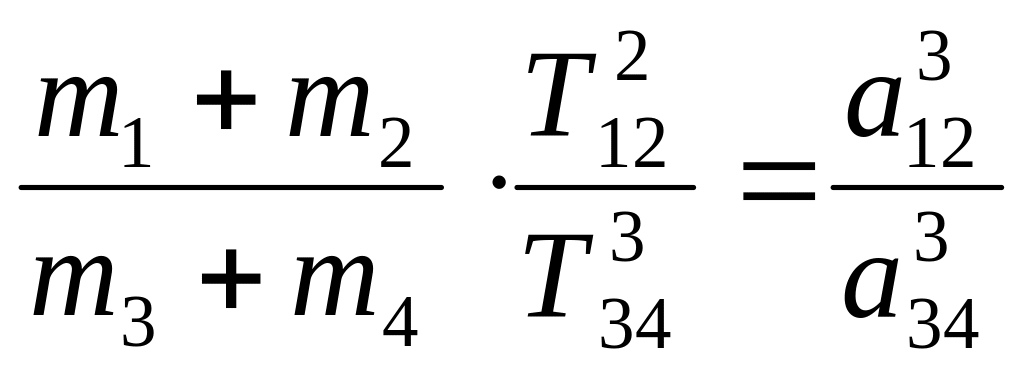. (4.38)

Выражение (4.38) является точной формулой третьего закона Кеплера. Третий уточненный закон Кеплера позволяет определить массу планеты, если у нее есть хотя бы один спутник. В (4.38) массы m_2,4 , как правило, пренебрегаемо малы по сравнению с массами m_1,3, следовательно, зная m₁ или m₃ можно вычислить вторую массу. Однако первоначально необходимо определить m какого либо тела в Солнечной системе, первоначально эта задача была решена для Земли.

Если у какого либо тела спутники отсутствуют, то его масса определяется другими методами, но на основе закона всемирного тяготения. Так массу Луны m_ определили по «лунному неравенству» в долготе Cолнца с месячным периодом. Это следствие того, что центр масс Земля-Луна находится на расстоянии 4650 км от центра Земли в сторону Луны. По приливам определили, что отношение масс Луна-Земля равно

.

По наблюдениям астероидов и затем ИСЗ оно получено как . С этим значением M_=333000m_ , M_≈2·10³³г .