4.6.2 Движение тела под действием силы тяготения

Если рассматривать движение планет или других тел (астероидов, комет) вокруг Солнца, то в большинстве случаев влиянием других тел («в первом приближении») можно пренебречь. В таком случае мы имеем дело с задачей двух тел. Математически строго эта задача решается путем интегрирования дифференциальных уравнений движения, получаемых из основного уравнения динамики материальной точки (4.14), в котором сила F есть сила тяготения. Это решение подробно рассматривается в курсах небесной механики или космической геодезии. Мы же получим основные выводы более простым путём.

Будем считать, что массы обоих тел сосредоточены в их центрах и следовательно их поле тяготения будет центральным или сферическим.

Пусть меньшее тело с масса m двигаясь в поле тяготения притягивающего тела с массой M имело в начальный момент скорость V₀ на расстоянии от r₀ от тела М (V₀ и r₀  начальные условия).

В дальнейшем используем закон сохранения энергии, который гласит, что

для изолированной физической системы энергия сохраняется с течением  времени.

Кинетическая энергия тела m равна

E_k=mV²/2, (4.21)

потенциальная энергия в центральном поле тяготения выражается формулой

E_p= fMm/r. (4.22)

Закон сохранения полной механической энергии для тела массой m, двигающегося в поле тяготения другого тела массой М запишется в следующем виде:

. (4.23)

В формуле (4.23) в левой части равенства стоит сумма кинетической и потенциальной энергий в начальный момент, а в правой  в любой другой момент времени. После сокращения на m и преобразований, мы получим интеграл энергии :

, (4.24)

Если заменить fM=K , то К  гравитационный параметр, зависящий от массы притягивающего тела, который для Солнца равен К=1,327210¹¹ км³/сек², то (4.25) можно записать

. (4.25)

4.6.2 Классификация орбит в задаче двух тел

Введём постоянную =const (постоянная для данной орбиты), тогда выражение (4.25) можно записать как

. (4.26)

В зависимости от значения, которое принимает h получим следующую орбиту:

а) круговая орбита

,

; (4.26а)

б) эллиптическая орбита

, ;

в) параболическая орбита

h=0, ;

г) гиперболическая орбита

h>0, .

П

Рис. 4.8 Типы орбит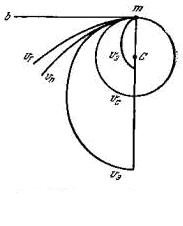

о круговым и эллиптическим орбитам движутся планеты, их спутники часть астероидов и периодические кометы. По параболическим и гиперболическим траекториям могут двигаться только непериодические кометы. На рис.4.8 приведён пример возможных траекторий движения тела m относительно центрального, находящегося в точке С, если начальная скорость направлена вдоль mb перпендикулярно mC. Если начальная скорость V₀ = V_C и будет направлена перпендикулярно к линии m_C, то точка m будет двигаться по кругу радиуса m_С. При V₀>V_П тело движется по гиперболе, при V₀=V_П  по параболе и при V₀<V_П  по эллипсу. При этом может быть два типа эллиптического движения, для которых точка С  ближний и дальний фокус от точки m. При дальнем фокусе орбита может быть получается незамкнутая, т.е тело m может упасть на М.