4.5 Элементы орбит.

Движение планеты или любого тела, вокруг центрального тела будет определено, если известна плоскость, в которой лежит её орбита, размеры и форма этой орбиты, её ориентировка в плоскости и, наконец, момент времени, в который планета находится в определённой точке орбиты. Величины, определяющие орбиты планеты, называются элементами орбиты.

v

r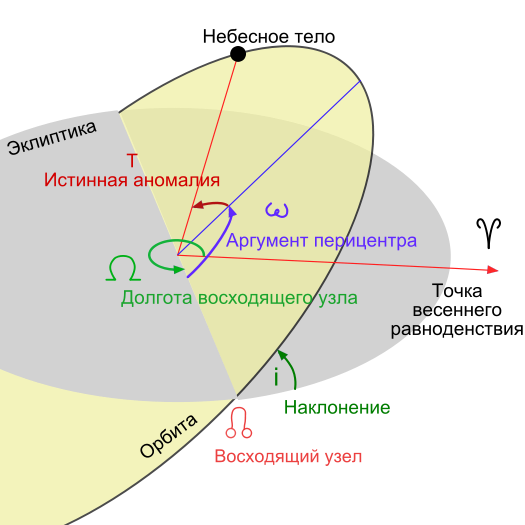

Рис. 4.7 Элементы орбит

Основных элементов 6 (Рис. 4.7):

1. наклон i плоскости орбиты к плоскости эклиптики 0°< i <180°, если 0°< i <180°, то движение прямое; если 90°< i <180° то движение обратное;

2. Долгота восходящего узла Ω; т. угол из центра О между положением на 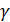(Т.В.Р) и восходящий узел орбиты Ω; 0°< Ω <360°, элементы i и Ω определяют положение плоскости орбиты в пространстве;

3) ω (аргумент перигея) – угловое расстояние перигелия (аргумент перигелия) от узла до линии апсид (угол из центра Солнца между  и П, он отсчитывается в плоскости орбиты планеты в направлении ее движения, 0°<ω<360°, величина ω определяет положение орбиты в ее плоскости;

4. а – большая полуось эллиптической орбиты, которая определяет звездный период обращения планеты.

5. эксцентриситет орбиты е = 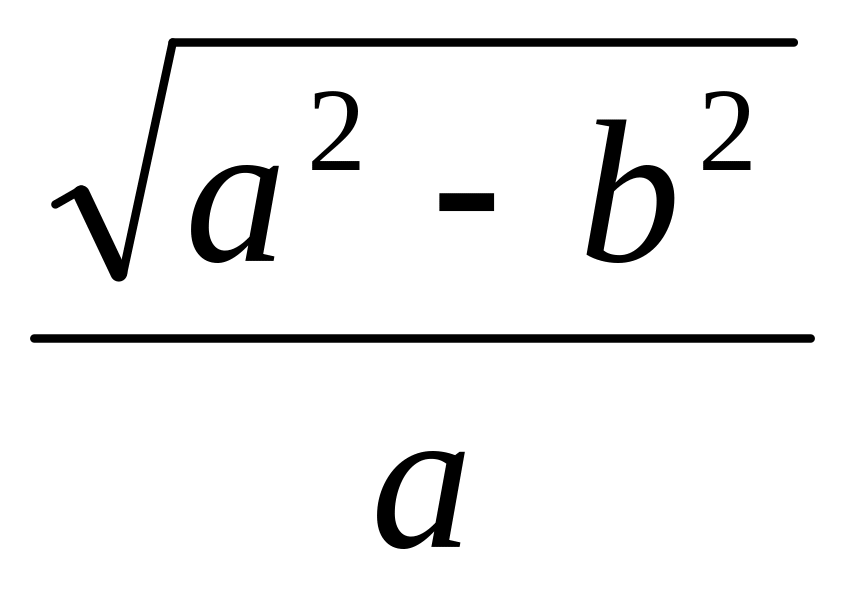, е – определяет форму эллипса, а и e определяют размеры и форму эллипса;

6. t₀ – момент прохождения через перигелий t₀, зная t₀ можно определить положение планеты на орбите в любой момент времени.

Положение планеты на орбите определяется двумя величинами: радиус – вектором r и истинной аномалией v, которые вычисляются по формулам, следующим из законов Кеплера,

r = α (1-ecosE); где E – эксцентрическая аномалия, Е=РОВ (рис. 4.5).

; (4.11)

где E – эксцентрическая аномалия, E находят из уравнения Кеплера методом последовательных приближений

M = E – esinE,

где M – средняя аномалии;

M = n(t t₀) = (t t₀), (4.12)

где n – среднее движение планеты, n= , Т  период обращения.

4.6 Закон всемирного тяготения

Законы Кеплера не объясняют причин движения. На первом этапе решения этой задачи потребовалось изучить законы движения. Трудами Галилея (1564 – 1642), Гюйгенса (1629 – 1695), Ньютона были сформулированы три закона движения (механики).

1. Всякое тело сохраняет состояние покоя или прямолинейного и равномерного движения, пока приложенные силы не заставят его изменить это состояние (закон инерции). Если m масса тела, а V скорость его движения, то математически закон инерции можно записать

mV=const . (4.13)

Если V=0, то находится в покое; если V= const  0, то тело движется равномерно и прямолинейно. Произведение mV называется импульсом или количество движения. Изменение импульса может произойти только под действием силы.

2. Изменение количества движения пропорционально приложенной силе и происходит по направлению вектора действия силы (основной закон динамики).

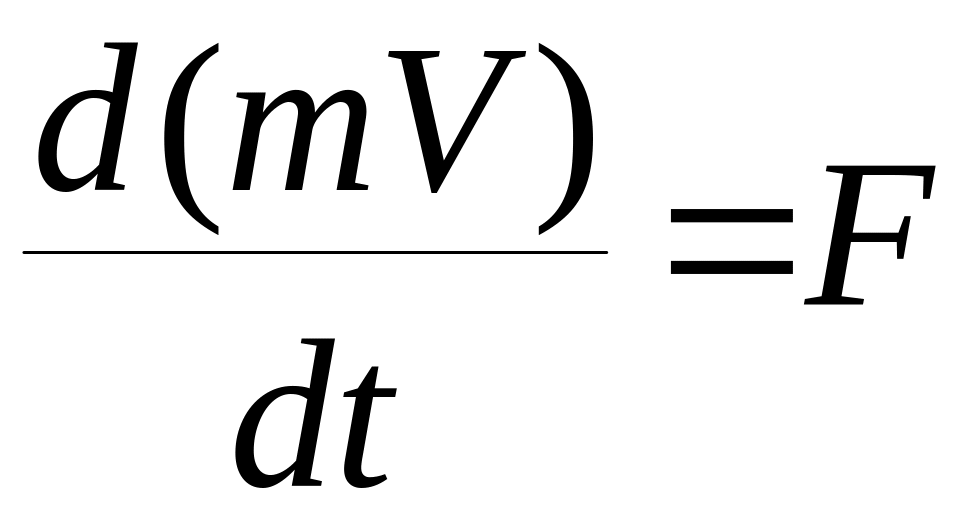
, (4.14)

или, если масса тела не меняется ,

F=mа, (4.15)

где а  ускорение.

т.е. произведение массы тела m на ускорение а равно действующей силе F.

3. Действие всегда вызывает равное по величине и противоположное по направлению противодействия

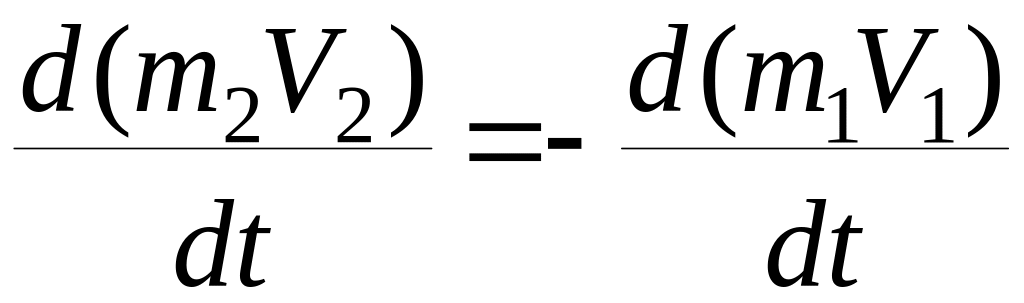; (4.16)

.

Эти законы позволили Ньютону сформулировать и математически доказать теорему. Ньютон доказал, что если движение математической частицы вокруг центра удовлетворяет закону площадей, то сила, отклоняющая это тело от движения по прямой линии, направлена точно к центру. Если движение планет вокруг Солнца удовлетворяет закону площадей, то движутся они под влиянием притяжения. Далее Ньютон доказал, что если планета движется вокруг Солнца по эллипсу, то притягиваемая сила убывает обратно пропорционально квадрату расстояний. Силы, которыми планеты отклоняются от прямолинейного движения и удерживаются на своих орбитах, направлены к Солнцу и обратно пропорциональны квадрату их больших полуосей. Доказав, что эта сила тождественна силе тяжести, действующей на поверхности Земли, Ньютон обобщил эту теорему и выразил ее в форме закона всемирного тяготения.

Каждые две частицы материи взаимно притягивают друг друга с силой прямо пропорциональной произведению их масс и обратно пропорционально квадрату расстояний между ними.

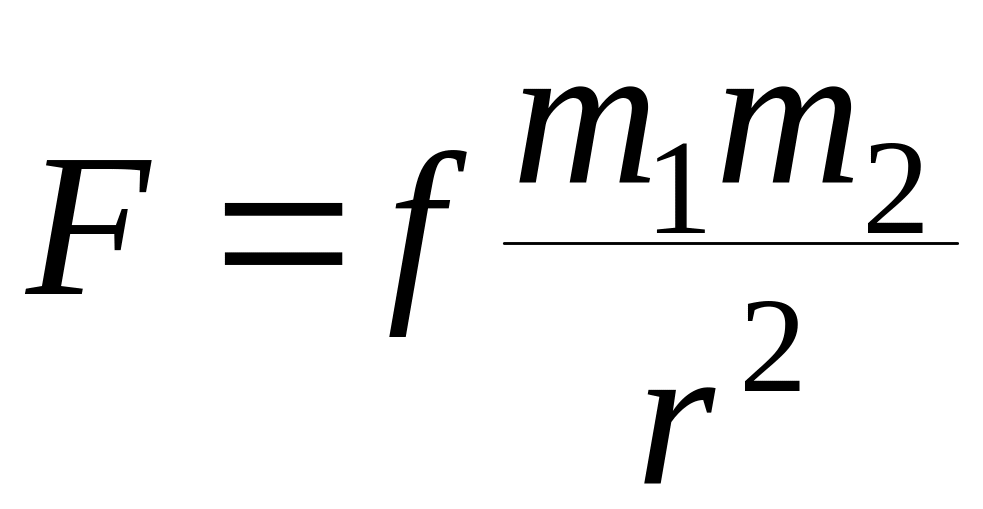(4.17)

где m₁ и m₂ массы тел, r – расстояние между ними, f – постоянная тяготения или гравитационная постоянная, которая по результатам последних определений имеет значение в CGS:

f = 6,6742810^-8 см³/ гсек² ;

в СИ:

f = 6,6742810^-11 м³/ кгсек².

Можно считать, что 2 частицы с массами m₁=m₂= 1г притягивают друг друга с F=(1/15)10^-6 дины.

В астрономии применяют следующие единицы: r – в астрономических единицах (а.е.), массу тел m в массах Солнца m_ʘ .

Закон тяготения Ньютона сформулирован для материальных частиц. Однако небесные тела — Солнце, Луна, планеты, звезды — не являются материальными частицами, они имеют значительные объемы. Но Ньютон доказал:

1) если два притягивающихся тела имеют форму шаров и равномерную плотность, то они притягиваются так, как будто их массы сосредоточены в их центрах;

2) так же притягиваются шаровые слои равномерной плотности, ограниченные двумя концентрическими шаровыми поверхностями;

3) так же притягиваются шары, плотность которых не везде одинакова, но вещество одинаковой плотности образует концентрические слои.

Для таких тел r в формуле (4.17) означает расстояние между центрами шаров; при этом радиусы шаров могут быть какого угодно размера по сравнению с расстоянием r, только их сумма должна быть меньше r. Так как подавляющее большинство небесных тел имеет почти правильную шаровую форму, с концентрическими слоями почти одинаковой плотности, а расстояние между их центрами значительно превосходит размеры шаров, то небесные тела можно рассматривать как материальные точки и при исследовании взаимодействий между ними пренебрегать на первом этапе уклонениями их формы от шарообразной. Заметные влияния подобных уклонений удобнее вычислять отдельно в виде «возмущений».