4.2 Прохождение внутренних планет по диску Солнца.

Вблизи двух узлов орбиты Меркурий и Венера для наблюдателя с Земли «проходят» по диску Солнца. Для Меркурия в среднем это происходит 14 раз за столетие.. Эти прохождения приходятся на ноябрь и май. За 217 лет происходит 9 майских и 20 ноябрьских прохождений  майские через 13 лет или через 33 года, ноябрьские через 7 или через 13 лет; после каждого майского через 3,5 года происходит ноябрьское прохождение Меркурия по диску Солнца. Последние прохождения: 7 мая 2003 г. и 8 ноября 2008 года, следующие: 9 мая 2016 г. и 11 ноября 2019 года.

Прохождение Венеры происходит не боле двух раз за столетие: через 105,5 лет, затем через 8, через 121,5, через 8 и вновь через 105,5 лет. Последние произошли 8.06.2004 (Рис. 4.3) и 5-6.06.2012 г., следующее произойдёт только в XXII веке.

Рис. 4.3 Прохождение Венеры по Солнцу 8 июня 2004 года

В 1761 году Ломоносов, наблюдая прохождение Венеры, открыл у нее атмосферу. Наблюдая моменты контактов Венеры с краем Солнца из различных пунктов, можно определить параллакс Солнца и расстояние от Солнца до Земли.

4.3 Периоды обращения планет: синодический, звездный (сидеричский)

Синодическим периодом обращения планеты (S) называют промежуток времени между двумя ее последовательностями одноименными конфигурациями.

Звездным (сидерическим) периодом (T) планеты называется промежуток времени, в течении которого планета совершает один оборот вокруг Солнца по своей орбите. Для Земли звездный период называется звездным годом (Т_).

Между этими периодами существует математическая связь.

Угловое смещение планеты за сутки равно , а у Земли , их разность есть видимое смещение планеты за сутки .

Отсюда уравнения синодического движения для нижних планет:

, после сокращения на 360 получим

(4.2)  уравнение синодического движения для нижней планеты.

Для верхней планеты запишем:

и далее

(4.3)  уравнение синодического движения для верхней планеты.

Синодический период можно определить из наблюдений, а звёздный только из вычислений, для земли Т_ = 365, 26 ср. солн. суток.

4.4 Законы Кеплера

Кеплер был сторонником гелиоцентрической системы мира Коперника, и, пытаясь усовершенствовать ее, взялся за обработку многолетних наблюдений планеты Марс, выполненных Тихо Браге и в течение нескольких лет самим И.Кеплером. Первоначально он пытался подобрать круговую орбиту (идеальное движение), но затем путем вычислений вывел, что форма орбиты  эллипс, плоскость которого проходит через Солнце, а само Солнце находится в фокусе эллипса, а движение происходит неравномерно. В начале 1607г. И.Кеплер сформулировал первые два закона:

1. Все планеты движутся по эллипсу вокруг Солнца в одном из фокусов которого (общем для всех планет) находится Солнце (рис.4.4 а)).

а) б)

Рис. 4.4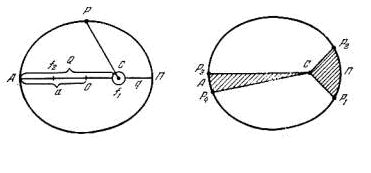

2. Радиус-вектор планеты за равные промежутки времени описывает равные площади.

Математически этот закон можно записать:

, (4.4)

где S  площадь сектора , t  промежуток времени (рис. 4.4 б)).

Кроме того Кеплер показал, что плоскости планетных орбит наклонены к эклиптике, причем у каждой планетной орбиты свой наклон.

В 1618г. Кеплер обнародовал свой третий закон планетных движений, выражавший связь между периодом планеты и величиной большой полуоси:

3. Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их эллиптических орбит.

(4.5)

Свои законы Кеплер вывел эмпирически, т.е. путем подбора не вскрывая причины такого движения.

Согласно 1-му закону орбита планет – эллипс, но эллипс есть геометрическое место точек (М), сумма расстояний которых до двух данных точек F₁, F₂ имеет одно и то же значение 2а, F₁М +F₂М = 2а где F₁, F₂  фокусы эллипса (рис. 4.5). Можно сказать, что сумма r₁+r₂=const .

Рис. 4.5 Эллипс

М

F₁

F₂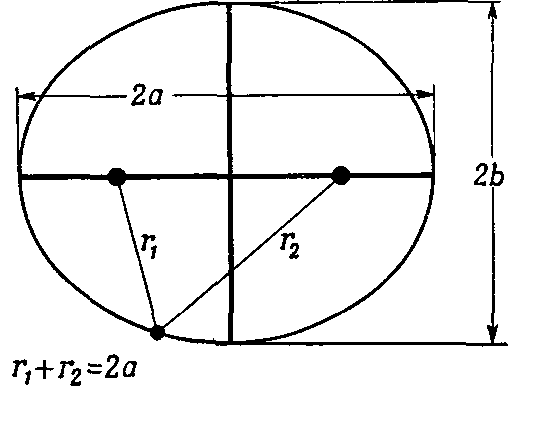

Движение планеты вокруг Солнца по законам Кеплера ещё называют невозмущенным движением. Путь планеты или другого небесного тела в пространстве называется орбитой. Орбита (орбитальный эллипс) (рис. 4.6) характеризуется определёнными параметрами:

 РО=АО  большая полуось а;

 в фокусе F₁ находится притягивающая масса  Солнце (S);

 ближайшая к Солнцу точка орбиты называется перигелий (Р), а наиболее отдаленная – афелий (А);

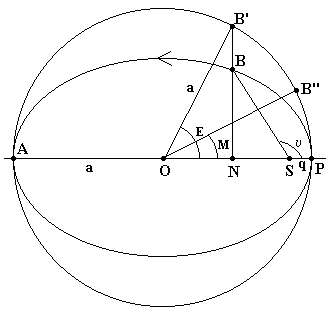
Рис. 4.6 Орбитальный эллипс

 (эксцентриситет), e – характеризует степень сжатия эллипса;

 большая ось орбиты АР называется линией (осью) апcид;

 отрезок, соединяющий фокус и планету (SB) называется радиус-вектор планеты (r).

Для расстояний от перигелия и афелия до главного фокуса существуют следующие соотношения :

ПS=a(1-e)=q ; (4.6)

AS=a(1+e)=Q ; (4.7)

, где а большая полуось, равная a=(q+Q)/2 .

Если V_cр средняя орбитальная скорость, то скорость в перигелии Р и афелии А будет равна:

; (4.8)

, (4.9)

для Земли V_сp =29,78 км/сек., эксцентриситет орбиты Земли . Если для Земли а=1 и Т=1, то для любой планеты .

(4.10)