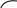- •Предисловие
- •1.Предмет и задачи астрономии, классификация разделов астрономии.
- •1.1 Задачи астрономии
- •1.2 Разделы астрономии
- •1.3 История и основные этапы развития астрономии
- •1.4 Связь астрономии с другими науками, практическое значение астрономии
- •Литература к разделу
- •2. Основные сведения о Вселенной, звездном небе, солнечной системе, Земле
- •2.1 Строение Вселенной
- •2.2 Созвездия
- •2.3 Видимое движение небесных светил
- •2.4 Общие сведения о Земле
- •2.5 Доказательство шарообразности Земли, её вращения вокруг оси и годичного движения вокруг Солнца.
- •2.6 Фигура и размеры Земли
- •Литература к разделу
- •3. Основы сферической астрономии
- •3.1 Основные понятия сферической тригонометрии
- •3.1.1 Свойства сферического треугольника
- •3.1.2 Решение сферического треугольника
- •3.2 Небесная сфера, основные точки и круги.
- •3.3 Системы небесных координат
- •3.3.1 Горизонтальная система координат
- •3.3.2 Первая экваториальная система координат
- •3.3.3 Вторая экваториальная система координат
- •3.3.4 Эклиптическая система координат
- •3.3.5 Географическая система координат
- •3.4 Связь между системами координат
- •3.4.1 Теорема о высоте полюса
- •3.4.2 Связь между географическими долготами и часовыми углами
- •3.4.3 Параллактический треугольник
- •3.5 Суточное вращение небесной сферы
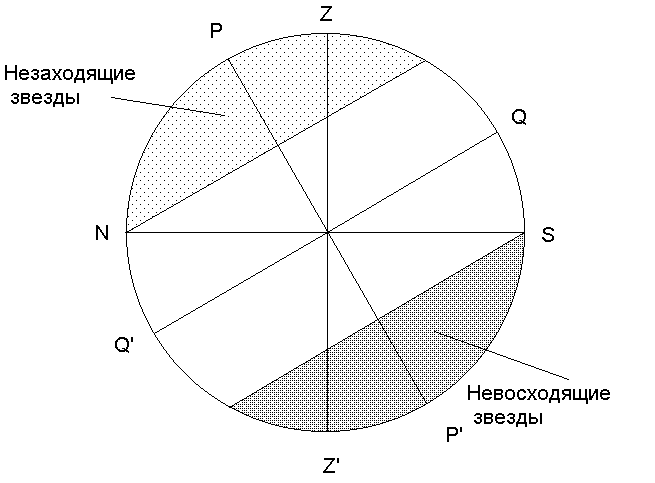
- •1.Незаходящие звёзды
- •2. Восходящие и заходящие звёзды
- •3. Невосходящие звёзды
- •3.6 Горизонтальные координаты светил в кульминациях
- •Для верхней кульминации
- •Для нижней кульминации
- •3.7 Движение Земли вокруг Солнца, изменение экваториальных координат Солнца в течение года.
- •3.8 Следствия годичного движения Земли вокруг Солнца, климатические пояса Земли.
- •3.9 Сумерки, белые ночи.
- •3.10 Время, системы измерения времени в астрономии.
- •3.10.1 Звездное время.
- •3.10.2 Солнечное время.
- •3.19 Связь среднего солнечного и звездного времени
- •3.10.3 Связь среднего солнечного и звездного времени.
- •3.10.4 Время на меридиане Гринвича
- •3.10.5 Время на разных меридианах
- •3.10.6 Поясное и декретное время
- •3.10.7 Эфемеридное время
- •3.10.8 Динамические шкалы времени
- •3.10.9 Атомное время
- •3.10.10 Всемирное координированное время.
- •3.10.11 Календарь
- •310.12 Юлианские дни
- •3.10.13 Линия перемены даты
- •3.11 Астрономические факторы
- •3.11.1 Рефракция
- •3.11.2 Параллакс
- •3.11.3 Аберрация
- •3.11.4 Прецессия и нутация
- •Литература к разделу
- •5. Астрономический календарь, постоянная часть/Под ред. В.К.Абалакина. Изд. 7-е, перераб.-л.: Наука, 1981.-704с.
- •Строение и масштаб солнечной системы, движение планет.
- •4.1 Видимое движение планет, конфигурации планет
- •4.2 Прохождение внутренних планет по диску Солнца.
- •4.3 Периоды обращения планет: синодический, звездный (сидеричский)
- •4.4 Законы Кеплера
- •Радиус-вектор планеты за равные промежутки времени описывает равные площади.
- •4.5 Элементы орбит.
- •4.6 Закон всемирного тяготения
- •4.6.1 Следствия закона всемирного тяготения
- •4.6.2 Движение тела под действием силы тяготения
- •4.6.2 Классификация орбит в задаче двух тел
- •4.7 Определение масс небесных тел
- •4.8 Движение исз
- •4.9 Орбита Луны и ее возмущения
- •4.10 Видимое движение и фазы Луны
- •4.11 Периоды обращения Луны
- •4.12 Вращение и либрации Луны
- •4.13 Затмения Луны и Солнца
- •Литература к разделу
- •5. Астрономический календарь, постоянная часть/Под ред. В.К.Абалакина. Изд. 7-е, перераб.-л.: Наука, 1981.-704с
- •5. Космонавтика
- •5.1 История
- •5.2 Значение освоения космоса
- •5.3 Сегодняшнее состояние космических программ и перспективы их развития
- •5.4 Ракеты-носители
- •5 .5 Вклад Кондратюка
- •Литература к разделу
- •Приложения Приложение 1 Приложении 1.1 Основные этапы освоения космоса
- •Приложение 1.2: Космические агентства
- •Приложение 1.3: Важные космические программы и полёты ка разных стран
- •1.3.1 Искусственные спутники Земли (исз)
- •1.3.2. Космические телескопы
- •1.3.3. Автоматические межпланетные станции
- •1.3.4. Лунные станции
- •1.3.5. Пилотируемые полёты
- •1.3.6. Орбитальные станции
- •1.3.7. Частные космические корабли
- •Приложение - 2
- •Iau Резолюция по планетам Резолюция 5a
3.4 Связь между системами координат
В астрономии используется несколько систем небесных и географическая система координат, поэтому между ними необходимо установить связь.
3.4.1 Теорема о высоте полюса
Г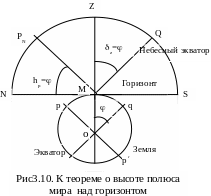 еографическая
широта места наблюдения численно равна
склонению зенита в точке наблюдения и
равна высоте полюса мира над горизонтом:
еографическая
широта места наблюдения численно равна
склонению зенита в точке наблюдения и
равна высоте полюса мира над горизонтом:
= z = hp.
Доказательство следует из рис.3.10. Географическая широта есть угол между плоскостью земного экватора и отвесной линией в пункте наблюдения, Moq. Склонение зенита z есть угол между плоскостью небесного экватора и отвесной линией, ZMQ. Склонение зенита и широта равны как соответствующие углы при параллельных прямых. Высота полюса Мира, hp=PNMN, и склонение зенита z равны
между собой как углы между взаимно перпендикулярными сторонами. Теорема 1 устанавливает связь координат географической, горизонтальной и экваториальной систем, на ней основано определение географических (астрономических) широт.
3.4.2 Связь между географическими долготами и часовыми углами
Разность часовых углов одного и того же светила, измеренная в один и тот же физический момент времени в двух различных точках земной поверхности численно равна разности географических долгот этих точек на земной поверхности:
t2 t1 = 2 1.
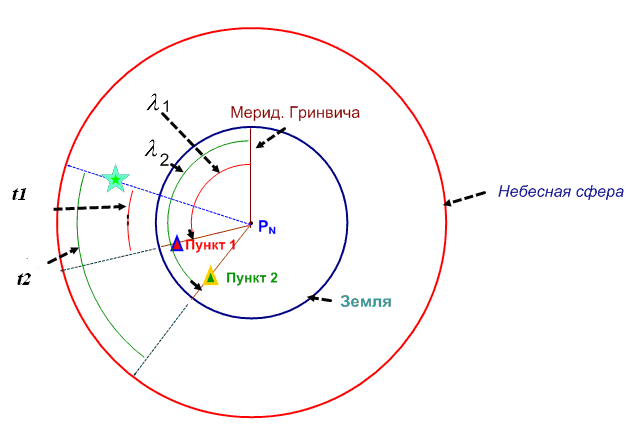
Рис. 3.11
Доказательство следует из рисунка 3.11, на котором изображена проекция Земли и небесной сферы на земной и небесный экватор с центром в полюсе мира и Земли (они совпадают). Разность долгот двух пунктов и разность часовых углов светила равна углу между меридианами этих пунктов, так как при таком проектировании небесные и земные меридианы совпадают. Далее, так как наблюдается одно и то же светило, то прибавив к часовым углам его прямое восхождение получим. Что разность долгот двух пунктов равна разности звёздных времён в них в один и тот же момент. Вторая теорема сферической астрономии положена в основу определения долгот пунктов.
3.4.3 Параллактический треугольник
В общем виде связь между астрономическими и географическими системами координат устанавливается через сферический треугольник на небесной сфере, который называется параллактический треугольник (рис. 3.12).
Определение. Параллактическим треугольником называется треугольник на небесной сфере, образованный пересечением небесного меридиана, вертикала и круга склонений светила. Его вершинами являются полюс мира Р, зенит Z и светил .
90-
Рис. 3.12 Параллактический
треугольник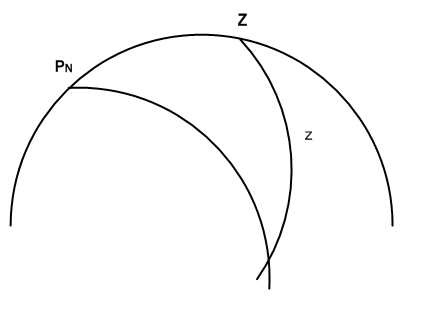
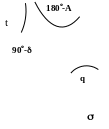
cosZ=sinj´sind+cosj´cosd´cost
-sinZ´cosA=sin
d
´cosj
cosdsinj´cost
sinZ´sinA=cosd´sint
sind=
sinj´cosZ+
cosj´sinZ´cosA
.
На этих формулах основаны способы определения астрономических координат и азимутов направлений.
3.5 Суточное вращение небесной сферы
Вследствие суточного вращения небесной сферы все светила описывают круги, плоскости которых параллельны плоскости небесного экватора, т.е. они движутся по суточным параллелям.
Каждое светило при суточном движении дважды проходит меридиан. Момент прохождения светилом небесного меридиана называется кульминацией светила. Кульминация называется верхней, если светило пересекает верхнюю часть меридиана PZQSP', в которой находится точка зенита Z, и нижней, если светило пересекает небесный меридиан в его нижней части PNQ'Z'P', содержащей точку надира Z'. В том случае, когда нижняя кульминация происходит над горизонтом (h > 0), такое светило называется незаходящим, а если даже во время верхней кульминации светило находится под горизонтом (h < 0), то оно называется невосходящим. Таким образом, все светила на небесной сфере разбиваются на три большие группы незаходящие, невосходящие и светила, которые восходят и заходят (рис. 11). Принадлежность светила к той или иной группе определяется его склонением и широтой места наблюдения . (рис. 3.13).
90
Рис. 3.13 |
Принадлежность звёзд к той или иной группе определяется из следующих соотношений: