3.3.3 Вторая экваториальная система координат

Во второй экваториальной системе координат основной плоскостью, как и в первой, является плоскость небесного экватора, а началом отсчета  точка весеннего равноденствия (рис. 3.6). Первой координатой также является склонение . Второй координатой, прямым восхождением , является дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, отсчитываемая против часовой стрелки. Как и часовой угол, прямое восхождение измеряется в часовой мере.

Рис.3.6 Вторая экваториальная система координат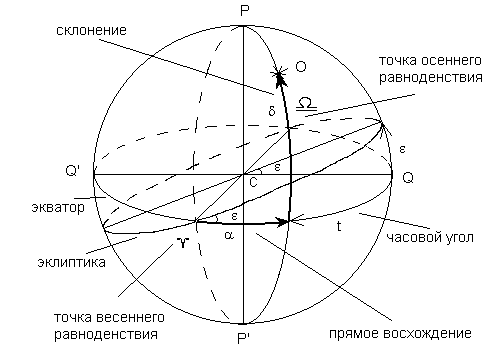

Сумма часового угла светила и его прямого восхождения называется звёздным временем и обозначается s или S. Ещё одно определение звёздного времени  часовой угол точки весеннего равноденствия является мерой звездного времени s:

s = t_ = t + .

Более подробно о звёздном времени будет сказано в разделе 3.11.

3.3.4 Эклиптическая система координат

Главной плоскостью в эклиптической системе координат является плоскость эклиптики. Северный полюс эклиптики обозначим через П_N; по определению дуга P_NП_N    равна примерно 23,5°.   Южный полюс эклиптики обозначим как П_S, а П_NП_S - ось эклиптики (рис. 3.7).

Линия пересечения двух плоскостей - небесного экватора и эклиптики называется линией узлов. Эклиптика делит небесную сферу на два полушария: северное и южное.

Большой круг, проведенный через полюсы эклиптики и небесный объект, называется кругом широты. Дуга круга широты AS , отсчитываемая от плоскости эклиптики, называется эклиптической широтой . Широта положительна в северном и отрицательна в южном полушарии.

Второй координатой является эклиптическая долгота l, равная двугранному углу между большим кругом, который проходит через полюсы эклиптики и динамическую точку весеннего равноденствия, и кругом широты:

^A=l .

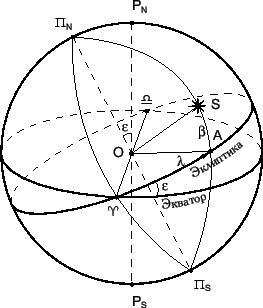
Рис.3.7 Эклиптическая система координат

Долгота измеряется от точки весеннего равноденствия от 0° до 360° против часовой стрелки, если смотреть с северного полюса

3.3.5 Географическая система координат

История появления географической системы координат уходит в глубину веков. Известно, что Гиппарх (2-ой век до н.э.) предлагал новые методы определения широты и долготы. Он же ввёл географическую сетку параллелей и меридианов. Способ определения широты по Солнцу был известен задолго до него. Необходимость определения координат точек земной поверхности скорее всего возникла при утверждении идей о шарообразности Земли.

Основные понятия географической системы координат. Ось вращения пересекает поверхность Земли в двух точках: в северном географическом полюсе РN и южном PS. Северный географический полюс тот, со стороны которого вращение Земли происходит против часовой стрелки. Большой круг на поверхности Земли q' G' O' q (рис.3.8а), плоскость которого перпендикулярна к оси вращения, называется земным экватором. Он делит поверхность Земли на два полушария: северное (с северным полюсом Р_N) и южное (с южным полюсом P_S).

Малые круги, плоскости которых параллельны плоскости земного экватора, называются географическими параллелями. Географическая параллель (bb), отстоящая на 23° 26' к северу от экватора, называется северным тропиком; параллель (cc), отстоящая на 23° 26' к югу от экватора, — южным тропиком. Географические параллели, отстоящие на 23° 26' от полюсов Земли, называются полярными кругами — северным (аа) и южным (dd). Положение этих кругов связано с наклоном оси вращения Земли к перпендикуляру к плоскости орбиты Земли на угол 23° 26'. Севернее северного полярного круга и южнее южного хотя бы раз в году наступает полярная ночь. Южнее северного тропика и севернее южного тропика Солнце в полдень хотя бы раз в году проходит зенит.

Пояс земной поверхности между тропиками (включая экватор) называется жарким или тропическим поясом. Пояс между северным тропиком и северным полярным кругом называется северным умеренным поясом, а между южным тропиком и южным полярным кругом — южным умеренным поясом. Области земной поверхности за полярными кругами называются северным холодным и южным холодным поясами.

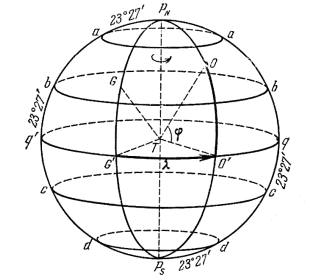
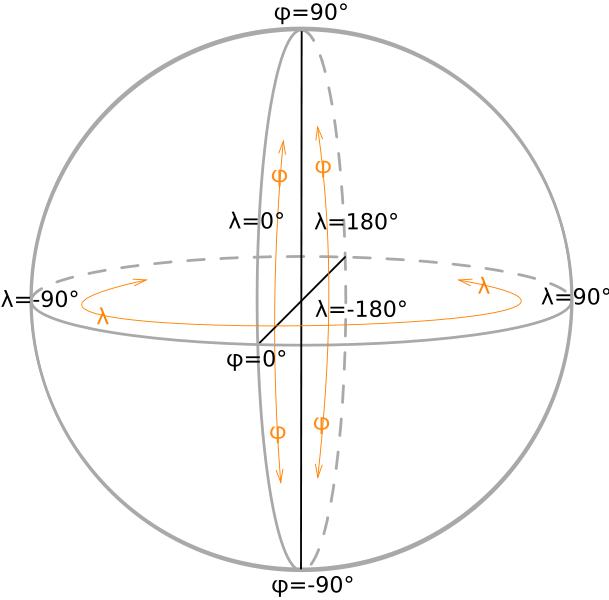
а) б)

Рис. 3.8 а,б

Большой полукруг PNOO'PS, проходящий через географические полюсы Земли и через точку О на ее поверхности, называется географическим меридианом точки О. Географический меридиан PNGG'PS, проходящий через Гринвичскую обсерваторию в Англии, считается нулевым или начальным меридианом. Нулевой меридиан и меридиан, отстоящий от нулевого на 180°, делят поверхность Земли на два полушария: восточное и западное. Прямая линия ТО, по которой направлена сила тяжести в данной точке Земли, называется отвесной или вертикальной линией.

Положение точки О на земной поверхности однозначно определяется двумя географическими координатами: географической широтой   и географической долготой  .

Географической широтой  точки О называется угол О’ТО между плоскостью земного экватора и отвесной линией, проходящей через точку О. Географические широты отсчитываются от экватора в пределах от 0° до +90° (северная широта), если точки лежат в северном полушарии Земли, и от 0° до —90° (южная широта), если точки лежат в южном полушарии.

Географической долготой  точки О называется двугранный угол G'TO' между плоскостями начального меридиана и меридиана, проходящего через точку О. В СССР и России принято отсчитывать географическую долготу к востоку от начального меридиана, т.е. в сторону вращения Земли, в пределах от 0° до 360° (в градусной мере), или от 0^h до 24^h (в часовой мере). В 1982 году решением XVIII Генеральной Ассамблеи (ГА) Международного Астрономического Союза (МАС) это правило принято для всех астрономических вычислений. Географы, как правило, отсчитывают долготу в пределах от 0 до +180° к востоку (восточная долгота) и от 0 до —180° к западу (западная долгота) (рис.3.8б).

При решении многих астрономических задач можно считать, что Земля представляет собой однородный шар радиусом R = 6370 км. В этом случае направление отвесной линии в любой точке земной поверхности проходит через центр Земли и совпадает с ее радиусом, а географические меридианы и экватор будут окружностями одинакового радиуса, равного радиусу Земли. И тогда географическая широта какой-либо точки на Земле может быть измерена дугой меридиана от экватора до данной точки, а географическая долгота — дугой экватора от начального меридиана до меридиана, проходящего через данную точку.

При решении задач, требующих более точных значений размеров и формы Земли, последняя принимается за эллипсоид вращения (сфероид) с неоднородным распределением масс. В этом случае отвесная линия не для всех точек земной поверхности будет проходить через центр сфероида Т (рис. 3.9), а будет пересекать плоскость земного экватора в некоторой другой точке T1, не совпадая с радиусом-вектором, т.е. с прямой ТО, соединяющей центр сфероида с точкой О.

Вследствие неравномерного распределения масс в области данной точки отвесная линия Т1O может также не совпадать и с нормалью Т2О к поверхности сфероида, т.е. с перпендикуляром к касательной плоскости в данной точке О Земли. По этому для каждой точки на поверхности Земли необходимо различать три вида географической широты: астрономическую, геоцентрическую и геодезическую.

Астрономической широтой  называется угол OT1q между плоскостью земного экватора и отвесной линией в данной точке.

Г еоцентрической широтой  называется угол OTq между плоскостью земного экватора и радиусом-вектором данной точки О.

Геодезической широтой В называется угол OT2q между плоскостью земного экватора и нормалью к сфероиду в данной точке.

Рис. 3.9

Непосредственно из астрономических наблюдений определяются только астрономические координаты  широта  и долгота . Из сравнения астрономических координат с геодезическими, а также из гравиметрических измерений определяется уклонение отвеса в данной точке, т.е. несовпадение отвесной линии с нормалью.

Астрономической широтой  называется угол OT1q между плоскостью земного экватора и отвесной линией в данной точке. Геоцентрической широтой  называется угол OTq между плоскостью земного экватора и радиусом-вектором данной точки О.Геодезической широтой В называется угол OT2q между плоскостью земного экватора и нормалью к сфероиду в данной точке. Непосредственно из астрономических наблюдений определяется только астрономическая широта . Из геодезических и гравиметрических измерений определяется уклонение отвеса в данной точке, т.е. несовпадение отвесной линии с нормалью, которое дает возможность из астрономической широты получить геодезическую. Уклонение отвеса, как правило, меньше 3" (исключая аномальные места), и в астрономических задачах ими пренебрегают и не делают различия между астрономической и геодезической широтой.

Геоцентрическая широта вычисляется по формулам аналитической геометрии, связывающим ее с астрономической (точнее, геодезической) широтой. Разность между геоцентрической и астрономической широтой не превышает 12'; на географических полюсах и на экваторе Земли она равна нулю.