4. Магнитные цепи
4.1. Понятие и назначение магнитных цепей
Магнитной цепью называется совокупность устройств, в которых образуется магнитный поток, сосредотачиваемый в определенной части пространства [1, 5]. Магнитные цепи – это магнитопроводы электрических машин, трансформаторов, измерительных приборов, магнитных усилителей, преобразователей частоты и других устройств, выполняемых из ферромагнитных материалов с высокой магнитной проницаемостью . В силу непостоянства магнитные цепи нелинейны.
Различают цепи с постоянными магнитами, в которых магнитные потоки создаются за счет остаточной намагниченности ферромагнитного материала, и цепи, в которых магнитные потоки возбуждаются токами катушек, охватывающих отдельные участки магнитопровода.
Магнитная цепь называется однородной, если она выполнена из одного ферромагнитного материала, и неоднородной, когда в магнитную цепь включены участки с различными магнитными свойствами, например, воздушный зазор или вставка из диамагнитного материала.
Магнитная цепь, во всех сечениях которой магнитный поток одинаков, называется неразветвленной. В разветвленной магнитной цепи потоки на различных участках неодинаковы. В этом случае используются понятия ветви и узла, аналогичные соответствующим понятиям электрической цепи.
Назначение магнитных цепей – усиление магнитного поля за счет намагничивающих свойств ферромагнитных материалов и сосредоточение его в определенном объеме.
Свойства ферромагнитных материалов характеризуются зависимостью магнитной индукции В от напряженности магнитного поля Н. Различают два основных типа этих зависимостей: кривые намагничивания и гистерезисные петли. Под кривой намагничивания понимают однозначную зависимость В(Н). На рис. 4.1 изображено семейство гистерезисных петель (частных циклов намагничивания). Геометрическое место вершин гистерезисных петель называют основной кривой намагничивания. При постоянных потоках используются именно основные кривые намагничивания, приводимые в справочниках в виде кривых и таблиц.
4 .2. Законы магнитных цепей при постоянных потоках
В основу расчета магнитных цепей положен один из фундаментальных законов электромагнетизма – закон полного тока в интегральной форме
(4.1)
с
Рис 4.1. Гистерезисная
петля
феромагнитного материала
(1
– основная кривая намагничивания)
по замкнутому контуру равна току,
охватываемому этим контуром. Вектор
имеет размерность ампер на метр (А/м).
В поле, создаваемом катушкой с w витками, циркуляция вектора напряженности определяется выражением:
(4.2)
где I – ток одного витка катушки.
Уравнение (4.2) сохраняет силу и для системы, в которой витки катушки расположены равномерно по сердечнику тороидальной формы, а контур интегрирования совпадает со средней линией тороида. Здесь напряженность одинакова по величине в любой точке контура, поэтому уравнение (4.2) принимает вид:
(4.3)
или
(4.4)
В одноконтурной магнитной системе, состоящей из n прямолинейных участков с разными поперечными сечениями, напряженность одинакова в пределах каждого участка средней линии. Поэтому можно записать:
(4.5)
где
– напряженность на отдельном участке;
– длина средней линии участка;
– намагничивающая или магнитодвижущая
сила, измеряемая в амперах (А).
Знак магнитодвижущей силы определяют по мнемоническому правилу охвата катушки правой рукой, расположив пальцы по направлению тока в катушке, при этом отогнутый большой палец показывает направление магнитодвижущей силы (рис. 4.2).
а б
Рис. 4.2. Определение знака магнитодвижущей силы
Произведение
в выражении (4.5) измеряется в амперах
(А) и рассматривается как разность
скалярных магнитных потенциалов или
падение магнитного напряжения на k-м
участке контура магнитной цепи:
(4.6)
С учетом соотношения (4.6) уравнение (4.5) принимает вид:
(4.7)
Уравнение (4.7) является аналогом второго закона Кирхгофа для контура электрической цепи.
С вектором
напряженности магнитного поля
связан вектор магнитной индукции
,
измеряемый в теслах (Тл):
(4.8)
где
– относительная магнитная проницаемость
(безразмерная величина);
– магнитная постоянная, равна 410-7,
Гн/м;
– абсолютная магнитная проницаемость,
Гн/м.
Через вектор магнитной индукции определяется скалярная величина – магнитный поток Ф, измеряемый в веберах (Вб):
(4.9)
Из интегральной формы выражения и принципа непрерывности магнитного поля, согласно которому поток вектора магнитной индукции через любую замкнутую поверхность равен нулю
(4.10)
следует уравнение для узла магнитной цепи:
(4.11)
Таким образом, в разветвленной магнитной цепи магнитный поток, подходящий к месту разветвления, равен сумме потоков, отходящих от места разветвления. В этом случае магнитный поток Ф, подобно току в электрической цепи, подчиняется первому закону Кирхгофа. Это выражение можно рассматривать как первый закон Кирхгофа для магнитной цепи.
По аналогии с электрическими цепями записывается и закон Ома:
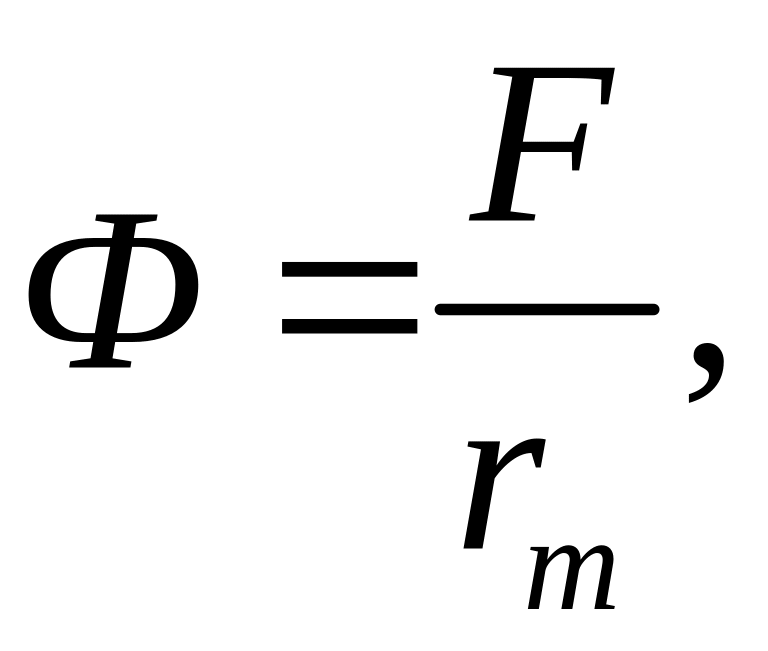(4.12)
где
– магнитное сопротивление контура
магнитной цепи, нелинейно зависящее от
магнитного потока. Измеряется в единицах
на генри (1/Гн).
Магнитное
сопротивление участка магнитопровода
длиной
с поперечным сечением S
можно определить по формуле:
. (4.13)
Для воздушных зазоров и вставок из диамагнитных материалов магнитная проницаемость принимается равной магнитной постоянной , связь между В и Н принимает вид:
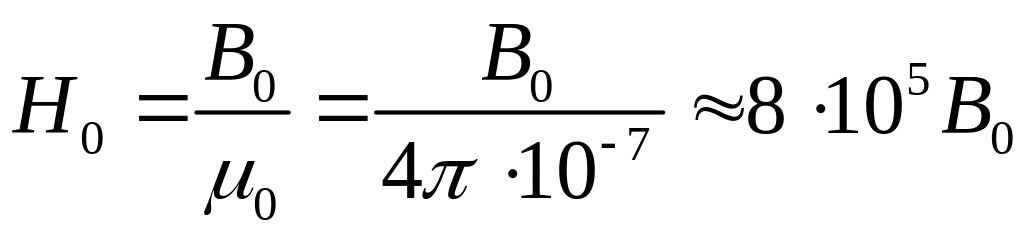, (4.14)
и магнитное
сопротивление
– постоянно.
Магнитный поток в цепи постоянен, если он образуется либо за счет введения в цепь постоянных магнитов, либо за счет использования в ней обмоток, обтекаемых постоянным током. При расчете таких цепей пользуются следующими допущениями:
1) в расчетах используется основная кривая намагничивания;
2) при наличии сердечника из ферромагнитного материала весь поток замыкается по сердечнику, т. е. не учитываются потоки рассеяния;
3) магнитная цепь разбивается на участки, выполненные из однородного материала, имеющие одинаковое сечение по всей длине, по которым проходит один и тот же поток;
4) на участках магнитной цепи магнитная индукция одинакова во всех точках поперечного сечения и нормальна к нему;
5) напряженность магнитного поля не изменяется по длине участка, которая принимается равной длине средней линии магнитной индукции и практи-чески не изменяется вдоль оси участка;
6) если участком является воздушный зазор, то его расчетное сечение принимается равным сечению соседних участков сердечника.