
- •Н. В. Пашкова, д. В. Пашков электротехника омск 2010
- •1. Цепи постоянного тока
- •1.1. Сведения из теории
- •1.1.1. Метод преобразования электрических цепей
- •1.1.2. Законы Кирхгофа
- •1.1.3. Баланс мощностей
- •1.2. Задание № 1 на расчет цепи постоянного тока
- •2. Цепи синусоидального тока
- •2.1. Сведения из теории
- •2.2. Задание № 2 на расчет цепи синусоидального тока
- •3. Нелинейные электрические цепи
- •3.1. Общие положения теории нелинейных электрических цепей
- •3.2. Графический метод расчета нелинейных электрических цепей постоянного тока
- •3.3. Задание № 3 на расчет нелинейной цепи постоянного тока
- •4. Магнитные цепи
- •4.1. Понятие и назначение магнитных цепей
- •4 .2. Законы магнитных цепей при постоянных потоках
- •4.3. Задание № 4 на расчет магнитной цепи постоянного тока
- •5. Катушка с ферромагнитным сердечником
- •5.1. Уравнение и схема замещения катушки с ферромагнитным сердечником
- •5.2. Задание № 5 на расчет цепи, содержащей катушку с ферромагнитным сердечником
- •6. Лабораторный практикум
- •6.1. Лабораторная работа 1 Линейные цепи постоянного тока
- •6.1.1. Цель работы
- •6.1.2. Особенности выполнения работы
- •6.1.3. Описание лабораторной установки
- •6.1.4. Опытная часть
- •6.1.5. Расчетная часть
- •6.2. Лабораторная работа 2 Линейные цепи синусоидального тока
- •6.2.3. Определение показаний приборов
- •6.2.4. Расчетная часть
- •6.2.5. Заключение по работе
- •6.2.6. Вопросы к защите работы
- •6.3. Лабораторная работа 3 Нелинейные цепи постоянного тока
- •6.3.1. Цель работы
- •6.3.2. План выполнения работы
- •6.3.3. Вопросы к защите работы
- •6.4. Лабораторная работа 4 Нелинейные элементы в цепях переменного тока
- •6.4.1. Цель работы
- •6.4.2. Особенности выполнения работы
- •6.4.3. План выполнения работы
- •6.4.4. Вопросы к защите работы
- •6.5. Лабораторная работа 5 Периодические процессы в нелинейных цепях переменного тока
- •6.5.1. Цель работы
- •6.5.2. Сведения из теории
- •6.5.3. План выполнения работы
- •6.5.4. Вопросы к защите работы
- •644046, Г. Омск, пр. Маркса, 35
1.1.3. Баланс мощностей
На основании закона сохранения энергии мощность, потребляемая в электрической цепи, должна быть равна мощности, поставляемой источниками. В состав потребляемой мощности входит мощность, рассеиваемая в сопротивлениях, а также мощность источников, находящихся в режиме потребителей.
Уравнение баланса мощностей имеет вид:
![]() (1.8)
(1.8)
или
![]() . (1.9)
. (1.9)
В левой части равенства (1.9) записана алгебраическая сумма произведений ЭДС источников на токи, протекающие через эти источники, и произведений токов источников тока на напряжения на их зажимах.
Примеры для определения знаков слагаемых приведены на рис.1.7.
В правой части уравнения баланса мощностей (1.9) записана арифметическая сумма произведений сопротивлений на квадраты токов, протекающих по этим сопротивлениям.

Рис.1.7. Примеры для определения знаков мощностей источников
Пример 3. Составить баланс мощностей для схемы, которая приведена на рис. 1.6. Дано: Е1 = 10 В; Е2 = 5 В; Е3 = 4 В; r1 = 5 Ом; r2 = 5 Ом; r3 = 1 Ом; r4 = 4 Ом; r5 = 2 Ом; r6 = 3 Ом; r6 = 5 Ом; I1 = 0,66 А; I2 = 0,87 А; I3 = 1,53 А; I4 = – 0,93 А; I5 = 0,27 А.
Решение.
![]() .
.
Подставляя значения
E,
r,
I
из данных
задачи, получаем суммарные мощности
источников и потребителей:
![]()
Расхождение между значениями мощности источников и потребителей определяется выражением:
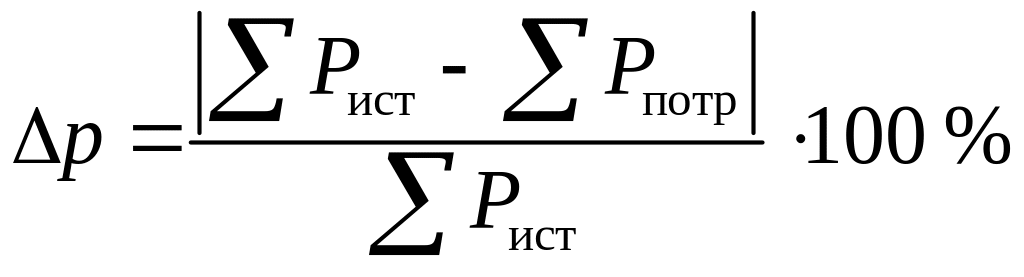 ;
;
 .
.
Данное расхождение не должно превышать 3 %. В данном случае можно считать, что баланс мощностей сходится.
1.2. Задание № 1 на расчет цепи постоянного тока
Условие задачи. В заданной цепи (рис.1.9, схемы 1 – 30) действует источник постоянной ЭДС Е. Определить значения тока ветвей и напряжение Uаb. Составить баланс мощностей и в общем виде уравнения по законам Кирхгофа для определения токов ветвей. ЭДС задана в вольтах, сопротивления – в омах. Ответ приведен под схемой.
В расчетной схеме, приведенной на рис. 1.8, задано: Е = 80 В; r1 = 20 Ом; r2 = 40 Ом; r3 = 15 Ом; r4 = 25 Ом; r5 = 20 Ом.

Рис.1.8. Расчетная схема для определения Uab
Решение.
Резистор r5
закорочен и поэтому в расчетах не
участвует, соответственно
![]() А.
А.
![]()
![]()

Рис.1.9. Расчетные схемы для определения значений тока и напряжения Uab
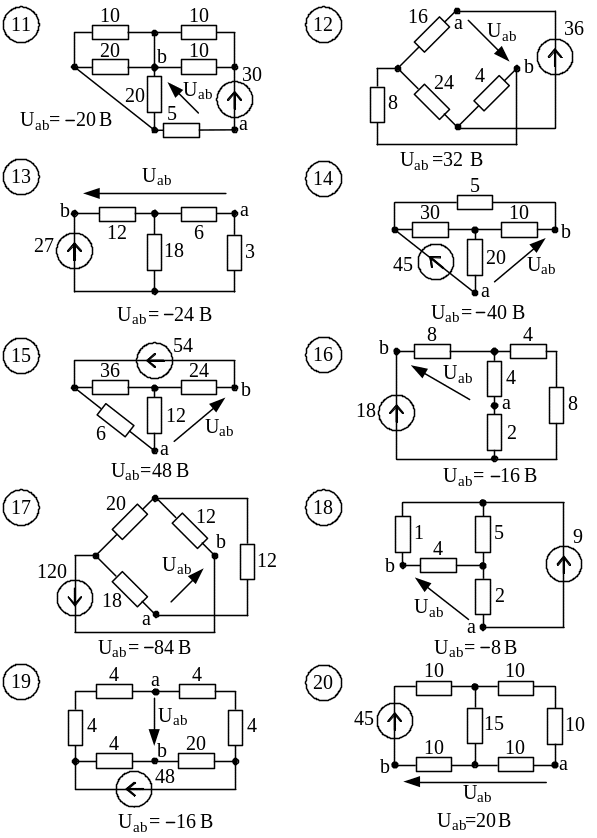
Рис. 1.9, лист 2

Рис. 1.9, лист 3

![]()
![]()
![]()

![]()
![]()
![]()
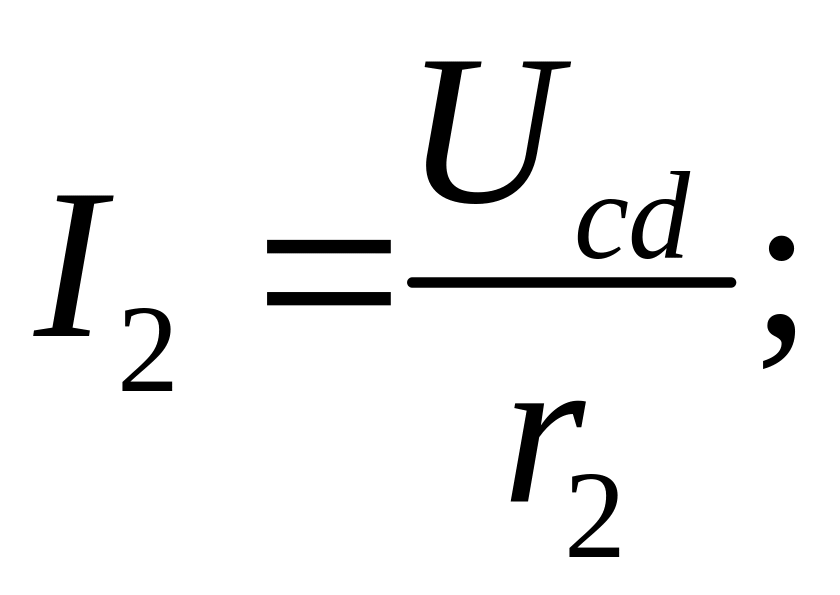
![]()
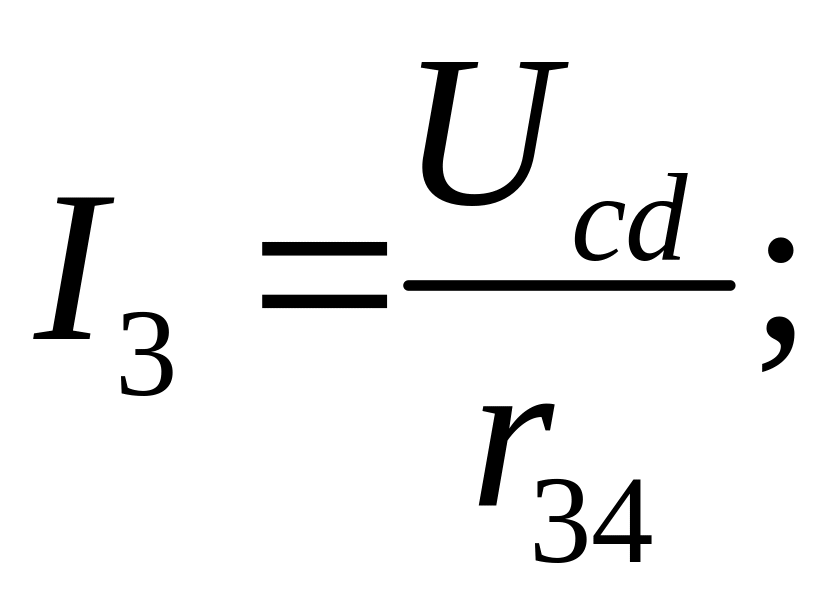
![]()
Напряжение Uab можно определить двумя способами –
а) через разность потенциалов:
![]()
Один из потенциалов
необходимо принять за ноль. Например,
![]() Тогда относительно этого потенциала
можно определить значения потенциалов
других точек, В:
Тогда относительно этого потенциала
можно определить значения потенциалов
других точек, В:
![]()
![]()
![]()
![]()
![]()
б) по второму закону
Кирхгофа, например, для контура аdbа
![]()
![]()
Отдаваемая
источником мощность
![]() Мощность потребителей
Мощность потребителей
![]() Так как
Так как
![]() ,
то имеет место баланс мощностей.
,
то имеет место баланс мощностей.
2. Цепи синусоидального тока
2.1. Сведения из теории
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону:
![]() (2.1)
(2.1)
где Im – максимальное значение или амплитуда тока;
![]() – угловая
частота;
– угловая
частота;
![]() – фаза;
– фаза;
![]() – начальная фаза.
– начальная фаза.
Угловая частота , частота f и период Т связаны соотношением:
![]() (2.2)
(2.2)
По выражению (2.1) на рис. 2.1,а построен график функции а на рис. 2.1,б – соответствующая векторная диаграмма.

Рис. 2.1. Синусоидальная функция и ее представление вращающимся вектором:
а – зависимость от времени; б – вращающийся вектор;
в – вектор на комплексной плоскости
Проекция вращающегося
против часовой стрелки с постоянной
угловой скоростью ω
вектора Im
(см. рис. 2.1,б) на вертикальную ось
изменяется во времени по синусоидальному
закону, поэтому любая синусоидальная
функция (ток, напряжение, ЭДС) может быть
изображена вектором. На рис. 2.1,в изображен
вектор тока с проекциями
![]() и
и
![]()
При проведении
расчетов удобным оказывается рассмотрение
вращающегося вектора
![]() на комплексной
плоскости. В этом случае вектор
можно
представить как комплексную амплитуду
тока
на комплексной
плоскости. В этом случае вектор
можно
представить как комплексную амплитуду
тока
![]() ,
а сам синусоидально изменяющийся ток
i(t)
– как мнимую
часть произведения комплексной
амплитуды на
,
а сам синусоидально изменяющийся ток
i(t)
– как мнимую
часть произведения комплексной
амплитуды на
![]() :
:
![]() , (2.3)
, (2.3)
тогда при t = 0 можно записать:
![]() (2.4)
(2.4)
На практике широкое
распространение получил символический
(комплексный) метод расчета [4] сущность
которого состоит в том, что при
синусоидальном токе можно перейти от
дифференциальных уравнений,
составленных для мгновенных значений,
к алгебраическим, составленным
относительно комплексов амплитудных
значений тока , напряжения
![]() ,
и ЭДС
,
и ЭДС
![]() либо их действующих значений
либо их действующих значений
![]() ,
,
![]() ,
и
,
и
![]() .
Например, если
.
Например, если
![]() , (2.5)
, (2.5)
то комплексное действующее значение напряжения
![]() (2.6)
(2.6)
где
![]()
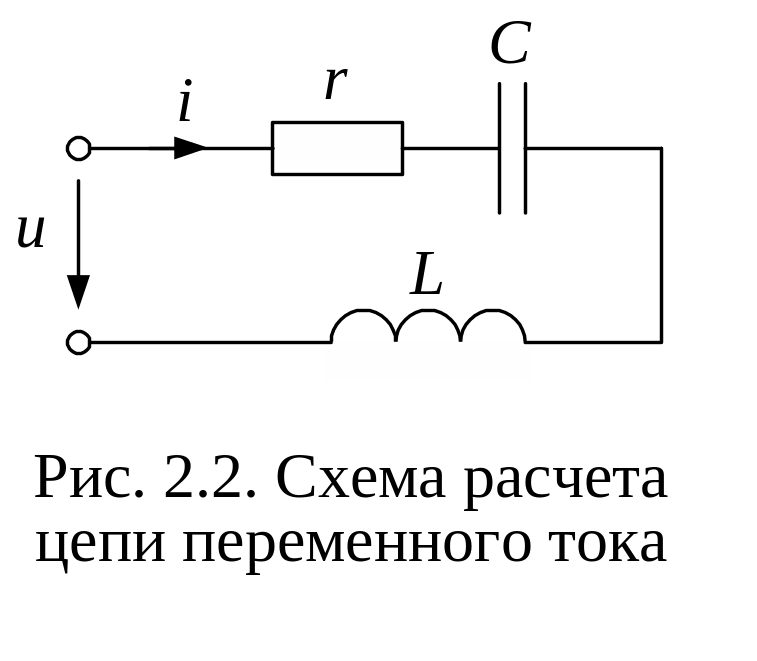
Аналогично осуществляется запись комплексов действующих значений ЭДС и тока. Например, для схемы (рис. 2.2) уравнение для мгновенных значений напряжений, составленное по второму закону Кирхгофа, запишется так:
![]()
 (2.7)
(2.7)
или
![]() (2.8)
(2.8)
Переходя к комплексным действующим
значениям напряжений, получим уравнение:
 (2.9)
(2.9)
где r – активное сопротивление цепи;
![]() – комплексное индуктивное сопротивление
цепи;
– комплексное индуктивное сопротивление
цепи;
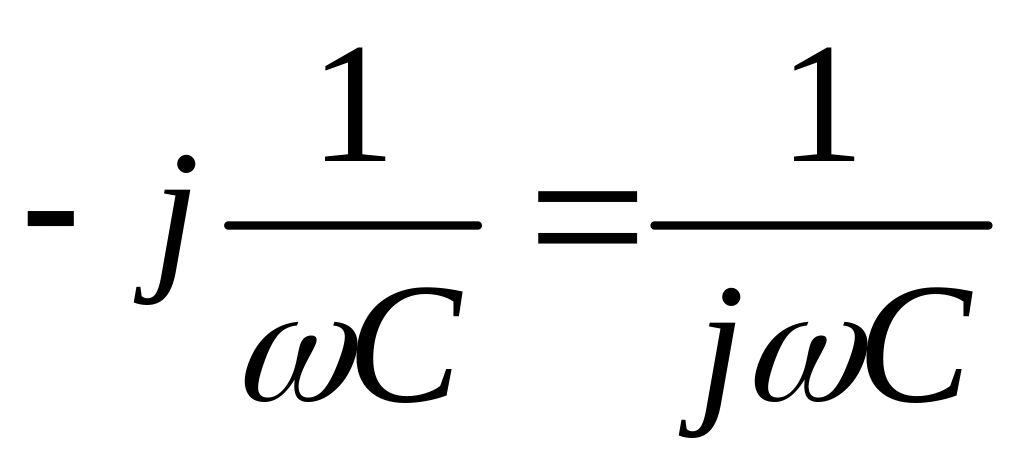 – комплексное
емкостное сопротивление цепи.
– комплексное
емкостное сопротивление цепи.
Множитель
![]() свидетельствует о том, что вектор
напряжения
свидетельствует о том, что вектор
напряжения
![]() на индуктивности L
опережает
вектор тока
на 90о.
Множитель
на индуктивности L
опережает
вектор тока
на 90о.
Множитель
![]() показывает,
что вектор напряжения
показывает,
что вектор напряжения
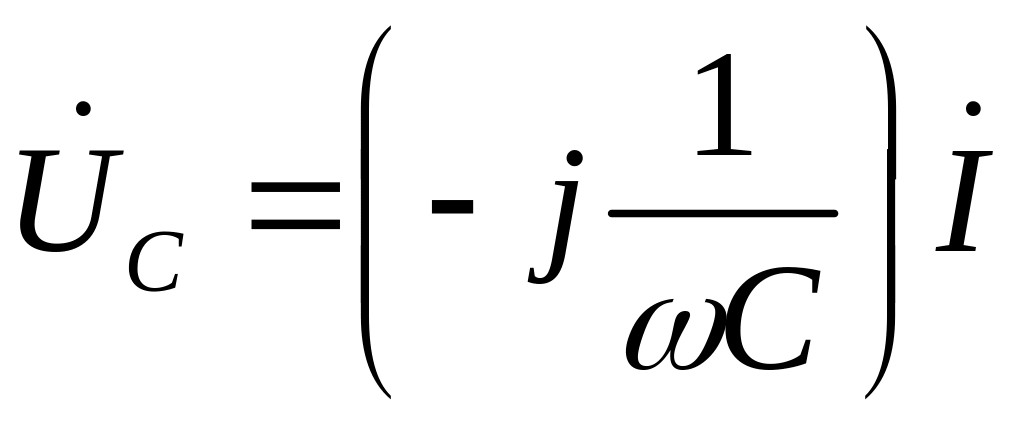 на емкости С
отстает от
вектора тока на 90о.
На активном сопротивлении r
векторы напряжения
на емкости С
отстает от
вектора тока на 90о.
На активном сопротивлении r
векторы напряжения
![]() и тока совпадают по направлению.
и тока совпадают по направлению.
Величина
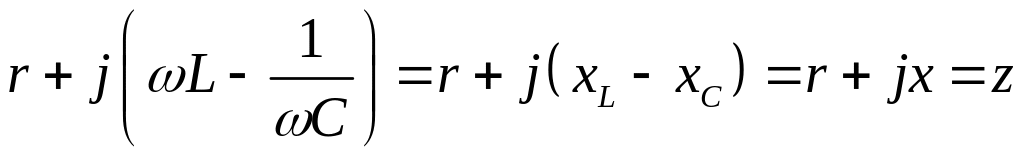 называется комплексным сопротивлением
цепи (см. рис. 2.2), а
называется комплексным сопротивлением
цепи (см. рис. 2.2), а
![]() – ее комплексной проводимостью, где g
и b
– активная и реактивная составляющие
проводимости цепи.
– ее комплексной проводимостью, где g
и b
– активная и реактивная составляющие
проводимости цепи.
Комплексные числа
записываются в одной из следующих форм:
алгебраическая –
![]() показательная –
показательная –
![]() ;
тригонометрическая –
;
тригонометрическая –
![]() полярная –
полярная –
![]()
Геометрически
любому комплексному числу А
можно
поставить в соответствие точку комплексной
плоскости
![]() с координатами
с координатами
![]()
![]() или радиус-вектор длиной а
единиц, проведенный из начала координат
в точку A
и расположенный под углом
к оси абсцисс (рис. 2.3).
или радиус-вектор длиной а
единиц, проведенный из начала координат
в точку A
и расположенный под углом
к оси абсцисс (рис. 2.3).
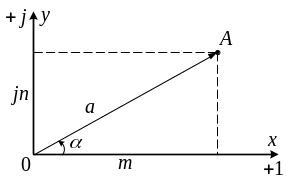
Рис. 2.3. Изображение числа на комплексной плоскости
Из рис. 2.3 очевидны
формулы перехода от одной формы записи
комплексного числа к другой:
![]()
![]()
![]() ;
;
![]()
А лгебраическая
форма применяется при сложении и
вычитании комплексных чисел, а
показательная – при умножении, делении,
возведении в степень и извлечении корня.
Умножение числа на мнимую единицу
лгебраическая
форма применяется при сложении и
вычитании комплексных чисел, а
показательная – при умножении, делении,
возведении в степень и извлечении корня.
Умножение числа на мнимую единицу
![]() сводится к повороту вектора на угол 90о
против часовой стрелки, умножение на
сводится к повороту вектора на угол 90о
против часовой стрелки, умножение на
![]() –
к повороту на угол 90о по часовой
стрелке (рис. 2.4), а умножению на –1
соответствует поворот на ±180о.
–
к повороту на угол 90о по часовой
стрелке (рис. 2.4), а умножению на –1
соответствует поворот на ±180о.
Полное комплексное сопротивление цепи Z и сопротивления ее участков (r, L и C) геометрически связаны треугольником сопротивлений (рис. 2.5, а, б):
а) если
![]() ,
то
,
то
![]()
![]() ;
;
б) если
![]() ,
то
,
то
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() .
.

а б
Рис. 2.5. Треугольники сопротивлений при нагрузке:
а – активно-индуктивной; б – активно-емкостный
Расчет электрической цепи в комплексной форме требует записи одного и того же комплексного числа в алгебраической и показательной форме.
Для расчета электрических цепей переменного тока символическим методом применяются все методы, описанные выше для цепей постоянного тока.
