
Вариант 16
Даны комплексные числа:
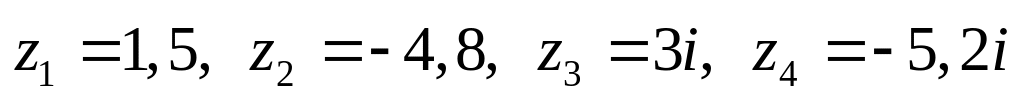 ,
,
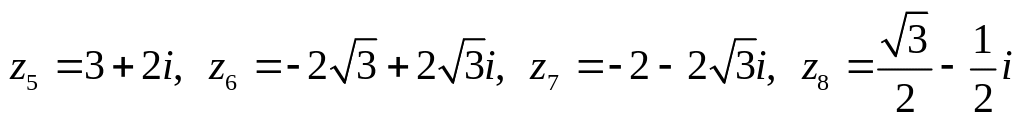 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
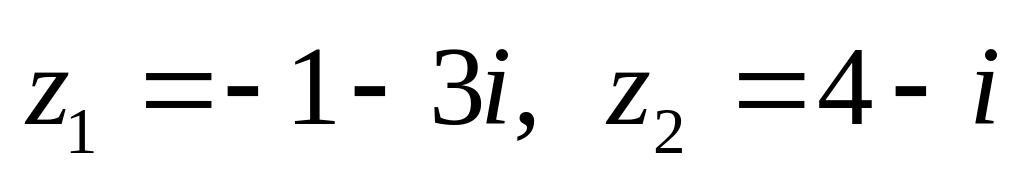 .
Вычислить
.
.
Вычислить
.Даны числа
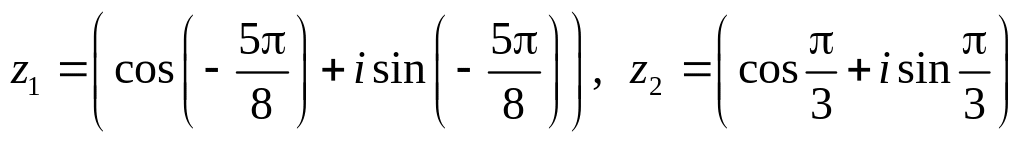 .
Вычислить
.
.
Вычислить
.Решить уравнение
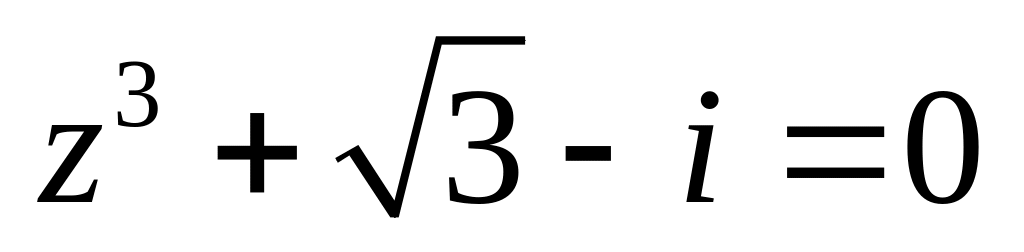 .
.Изобразить область, заданную неравенствами:
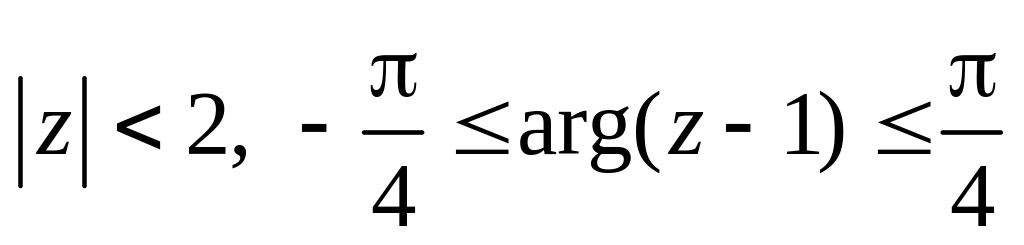 .
.
ВАРИАНТ 17
Даны комплексные числа:
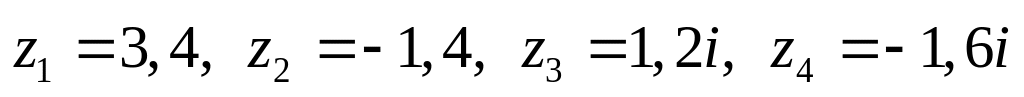 ,
,
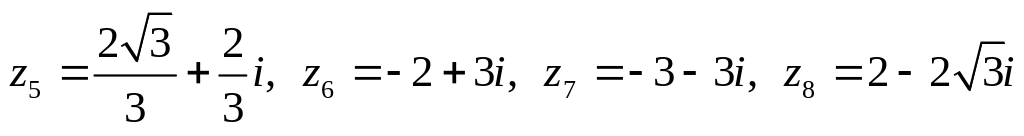 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
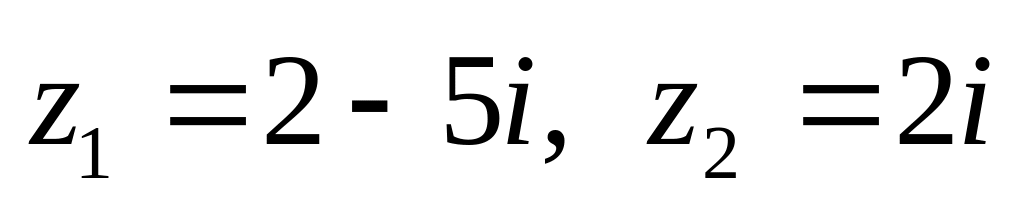 .
Вычислить
.
.
Вычислить
.Даны числа
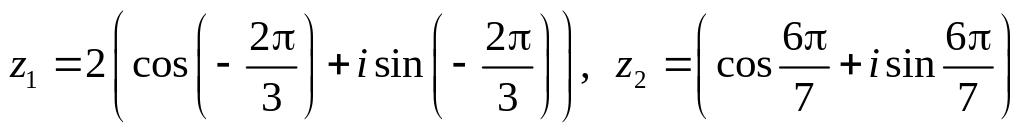 .
Вычислить
.
.
Вычислить
.Решить уравнение
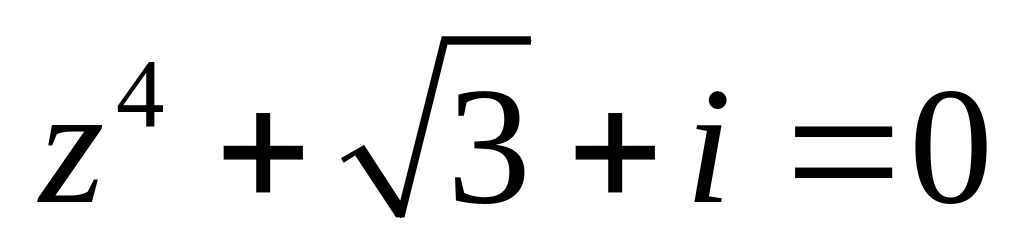 .
.Изобразить область, заданную неравенствами:
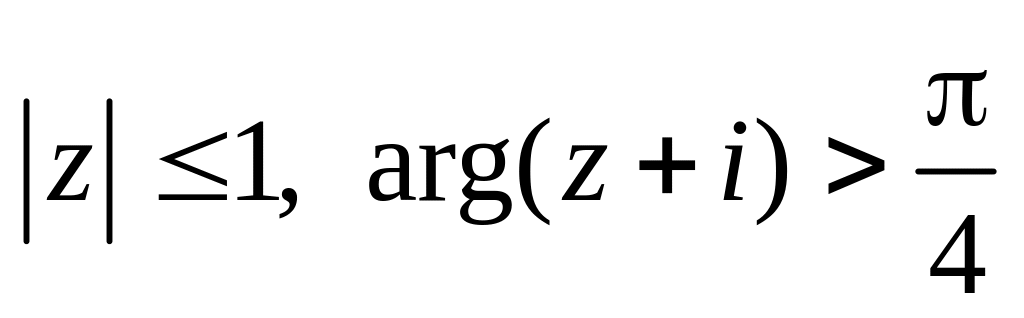 .
.
ВАРИАНТ 18
Даны комплексные числа:
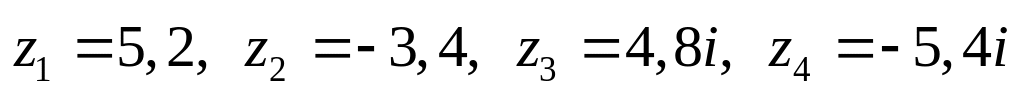 ,
,
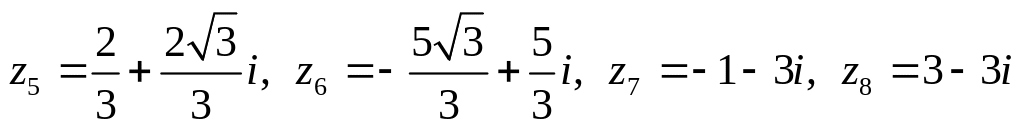 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
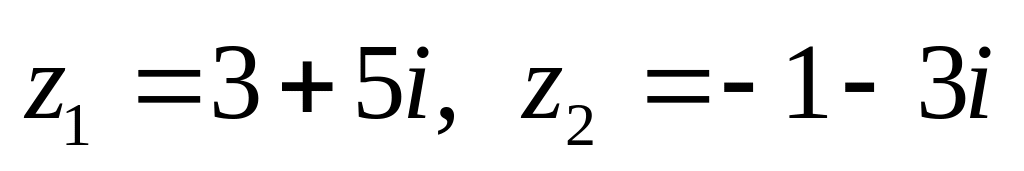 .
Вычислить
.
.
Вычислить
.Даны числа
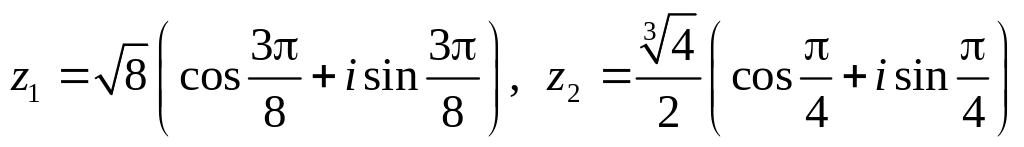 .
Вычислить
.
.
Вычислить
.Решить уравнение
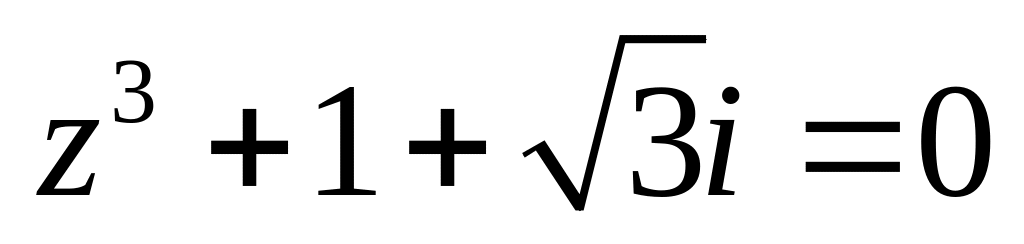 .
.Изобразить область, заданную неравенствами:
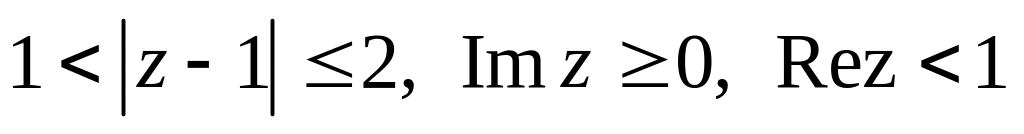 .
.
ВАРИАНТ 19
Даны комплексные числа:
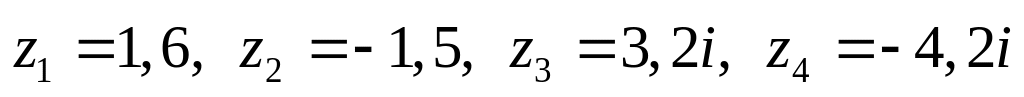 ,
,
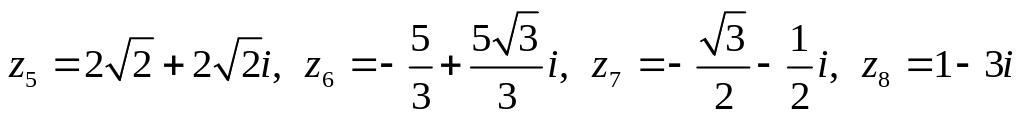 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
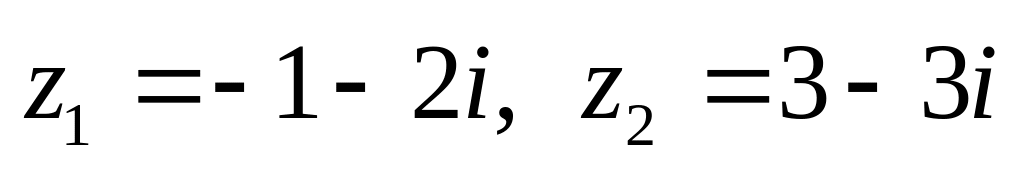 .
Вычислить
.
.
Вычислить
.Даны числа
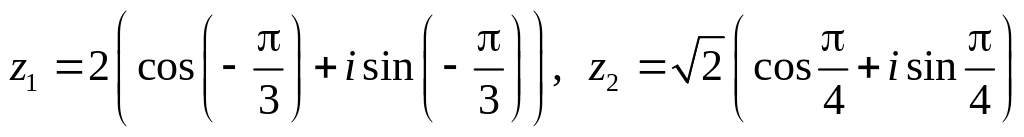 .
Вычислить
.
.
Вычислить
.Решить уравнение
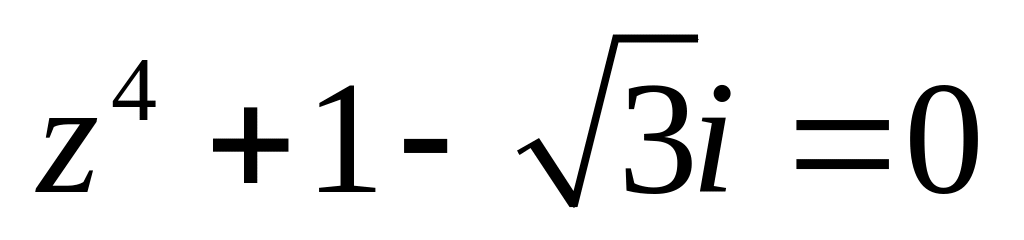 .
.Изобразить область, заданную неравенствами:
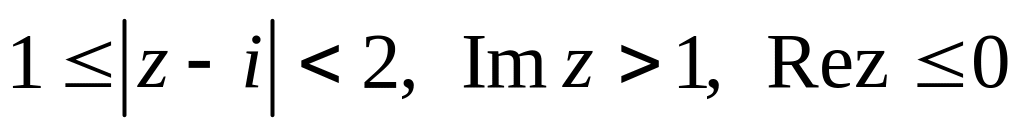 .
.
Вариант 20
Даны комплексные числа:
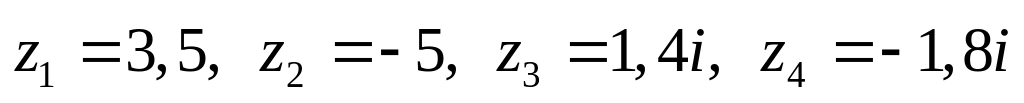 ,
,
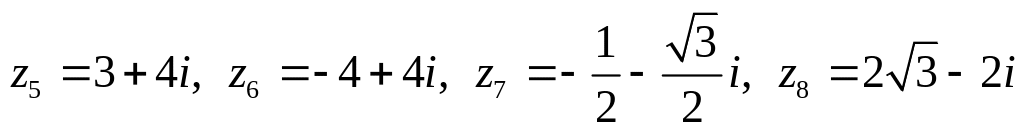 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
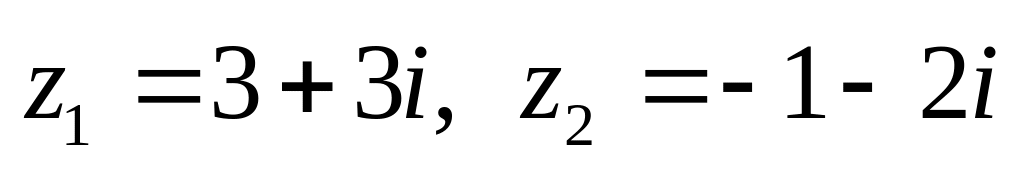 .
Вычислить
.
.
Вычислить
.Даны числа
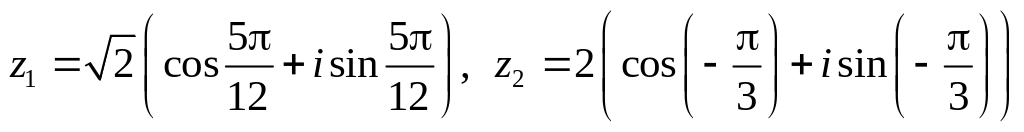 .
Вычислить
.
.
Вычислить
.Решить уравнение
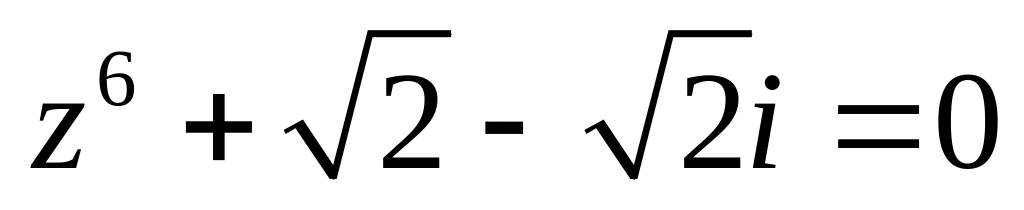 .
.Изобразить область, заданную неравенствами:
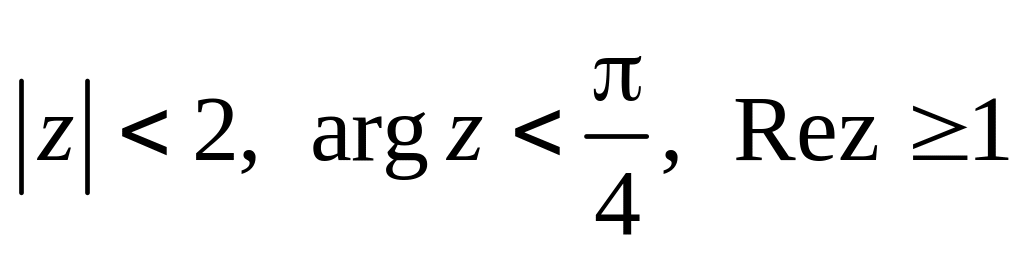 .
.
ВАРИАНТ 21
Даны комплексные числа:
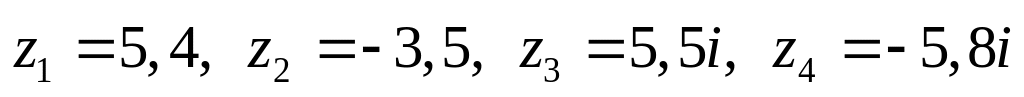 ,
,
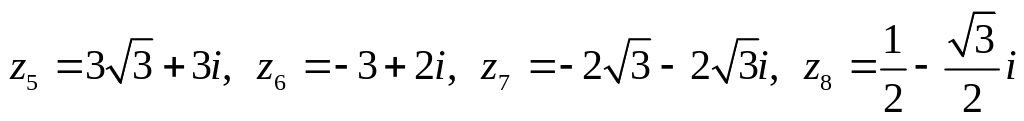 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
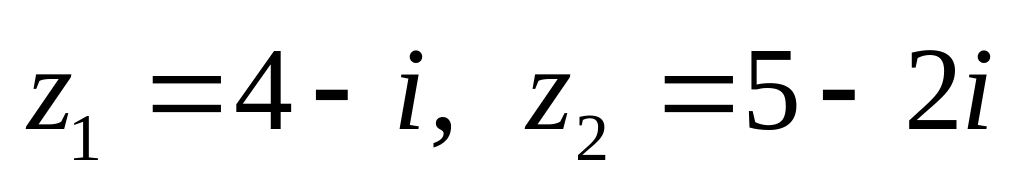 .
Вычислить
.
.
Вычислить
.Даны числа . Вычислить .
Решить уравнение
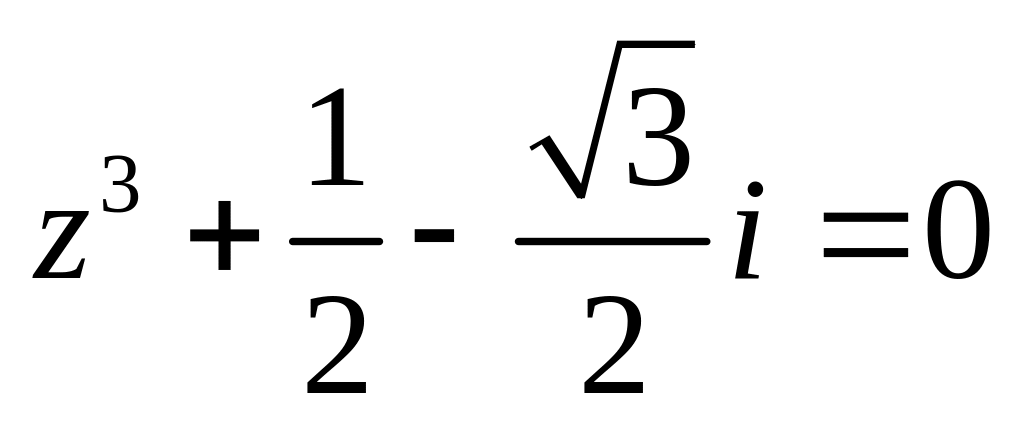 .
.Изобразить область, заданную неравенствами:
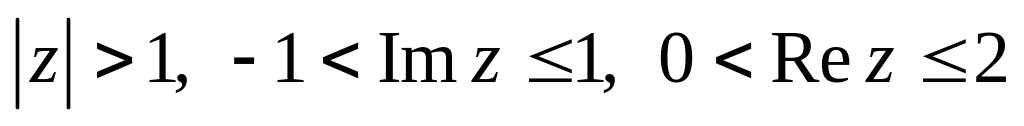 .
.
ВАРИАНТ 22
Даны комплексные числа:
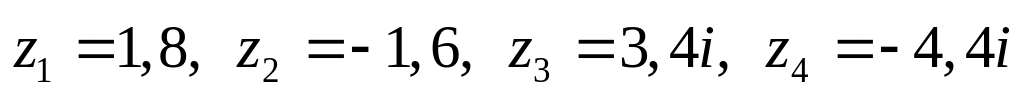 ,
,
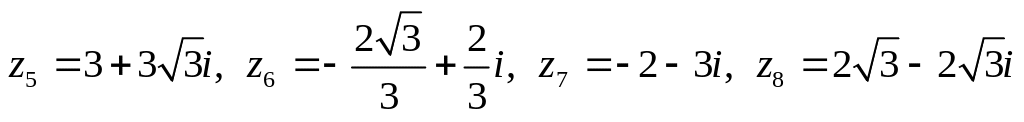 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
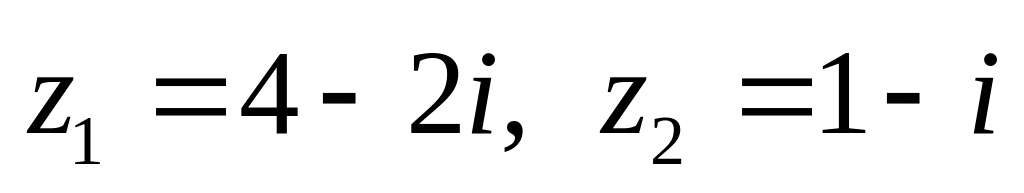 .
Вычислить
.
.
Вычислить
.Даны числа
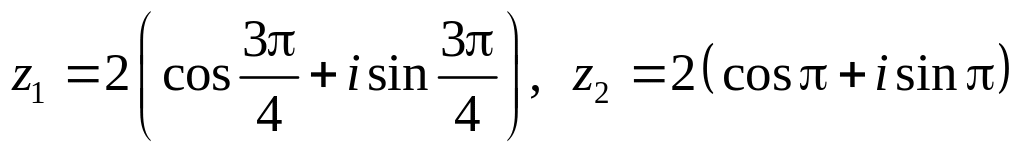 .
Вычислить
.
.
Вычислить
.Решить уравнение
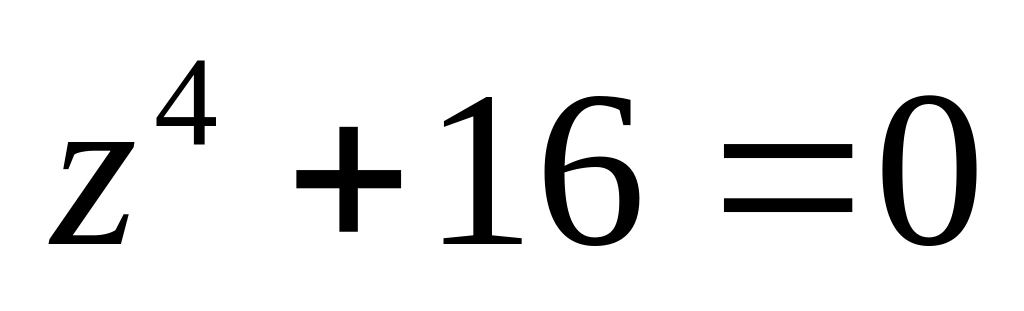 .
.Изобразить область, заданную неравенствами:
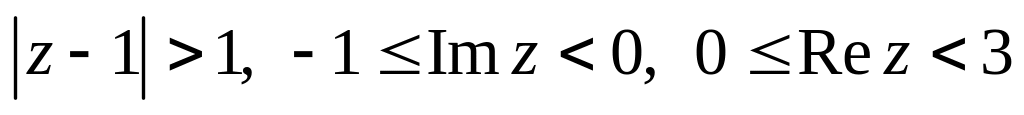 .
.
ВАРИАНТ 23
Даны комплексные числа:
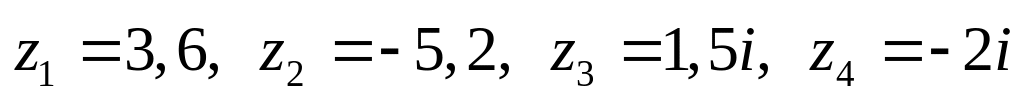 ,
,
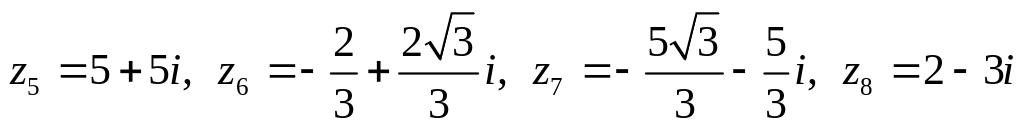 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
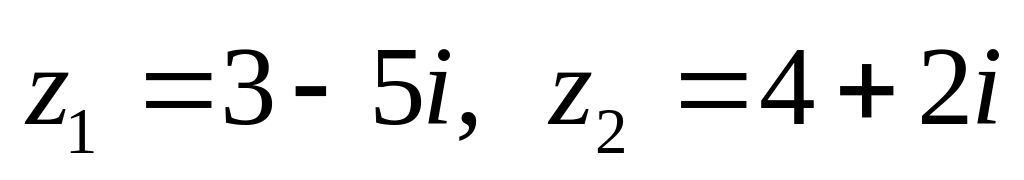 .
Вычислить
.
.
Вычислить
.Даны числа
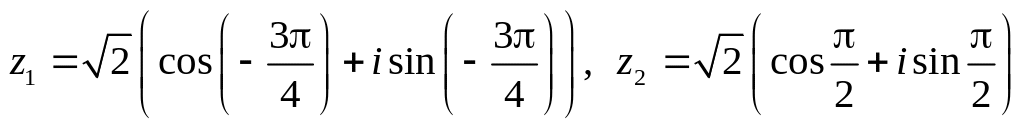 .
Вычислить
.
.
Вычислить
.Решить уравнение
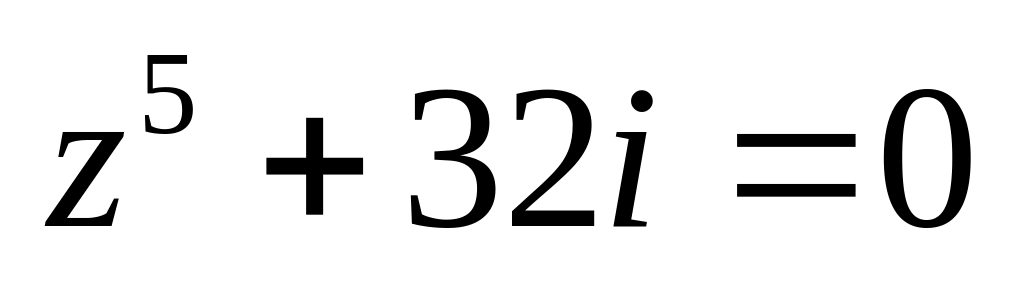 .
.Изобразить область, заданную неравенствами:
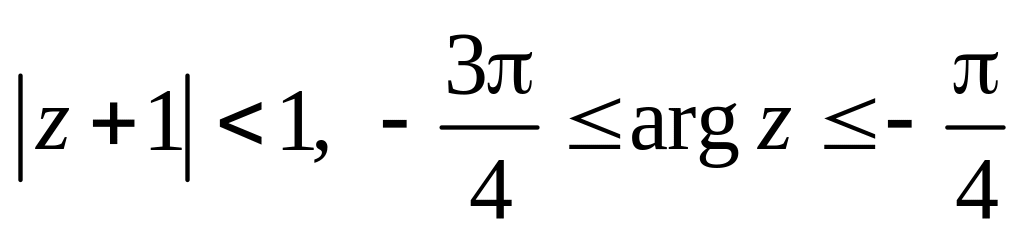 .
.
ВАРИАНТ 24
Даны комплексные числа:
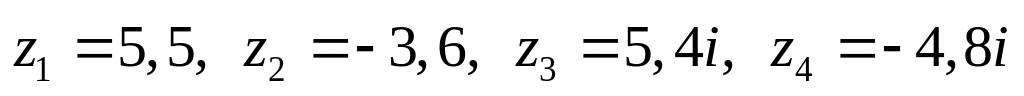 ,
,
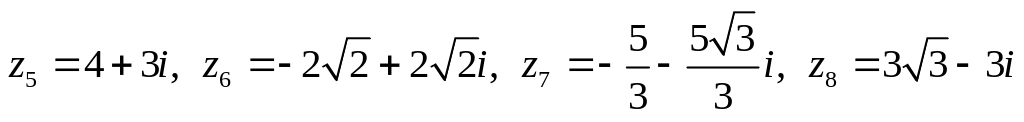 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
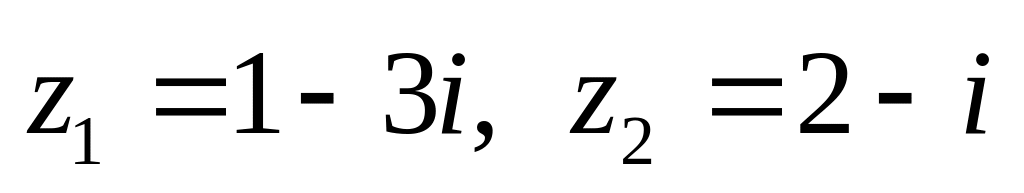 .
Вычислить
.
.
Вычислить
.Даны числа
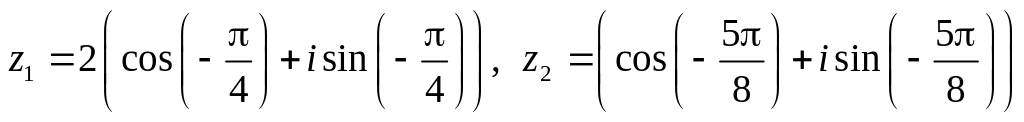 .
Вычислить
.
.
Вычислить
.Решить уравнение
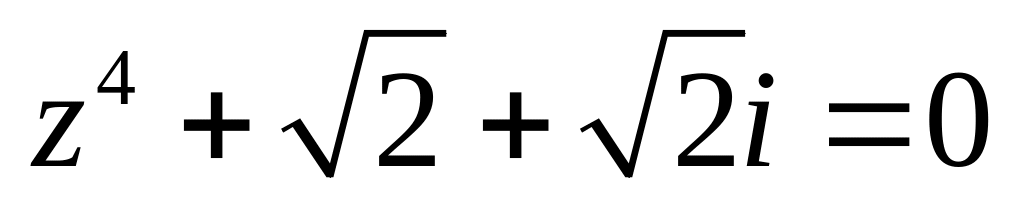 .
.Изобразить область, заданную неравенствами:
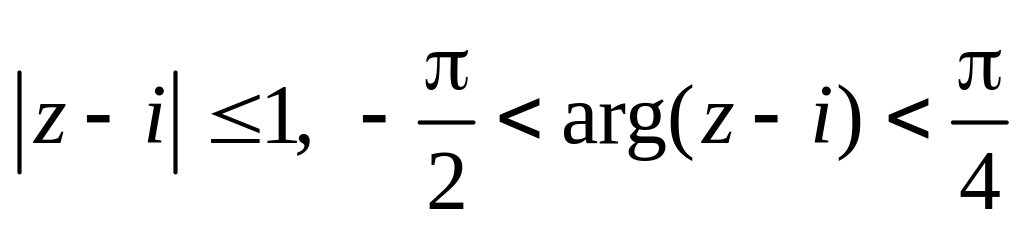 .
.
ВАРИАНТ 25
Даны комплексные числа:
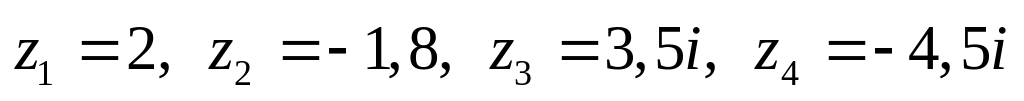 ,
,
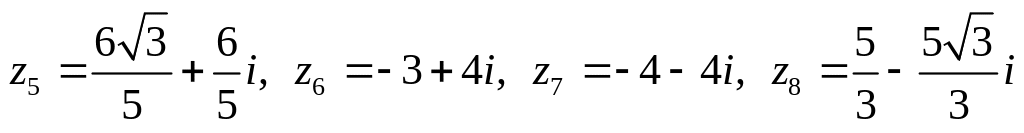 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
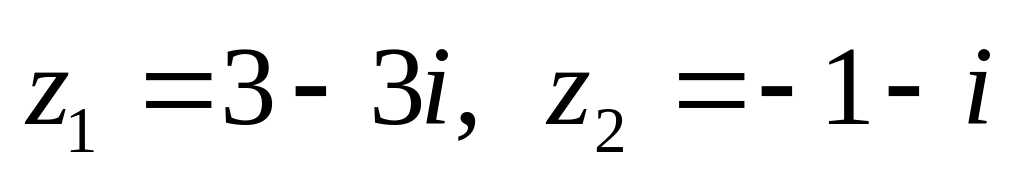 .
Вычислить
.
.
Вычислить
.Даны числа . Вычислить .
Решить уравнение
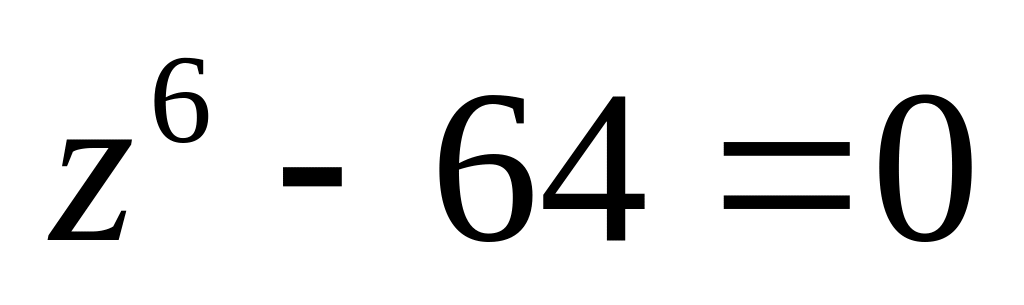 .
.Изобразить область, заданную неравенствами:
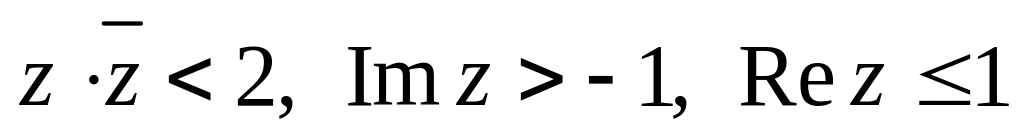 .
.
ВАРИАНТ 26
Даны комплексные числа:
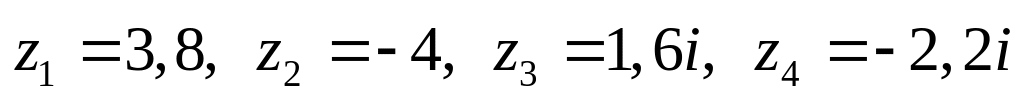 ,
,
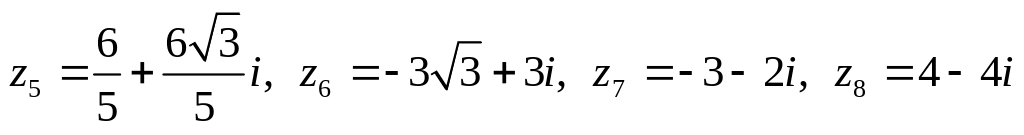 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
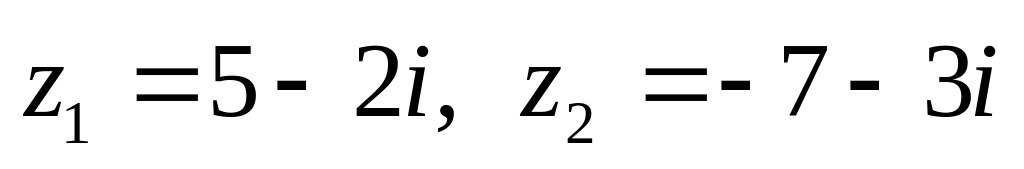 .
Вычислить
.
.
Вычислить
.Даны числа
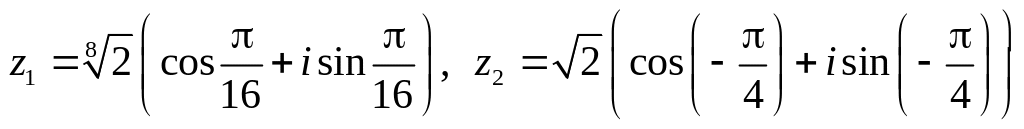 .
Вычислить
.
.
Вычислить
.Решить уравнение
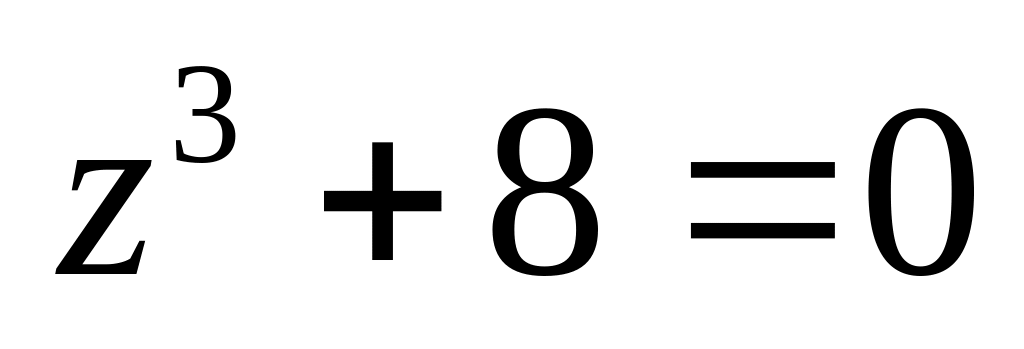 .
.Изобразить область, заданную неравенствами:
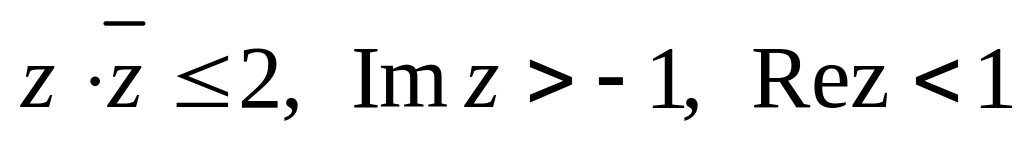 .
.
ВАРИАНТ 27
Даны комплексные числа:
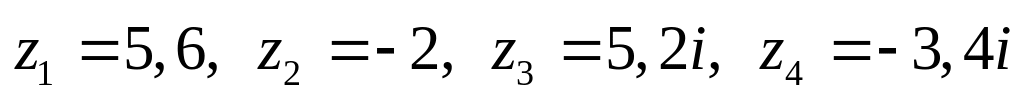 ,
,
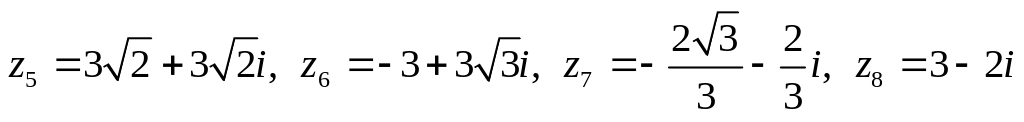 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
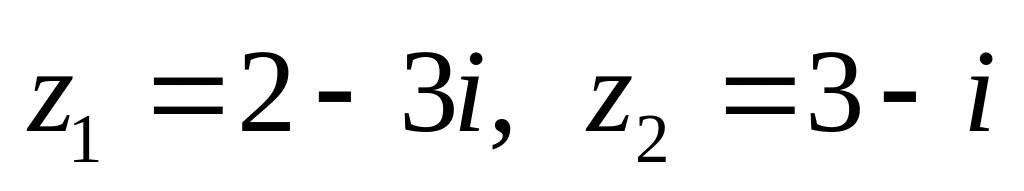 .
Вычислить
.
.
Вычислить
.Даны числа
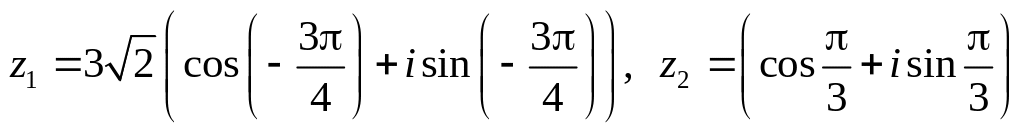 .
Вычислить
.
.
Вычислить
.Решить уравнение
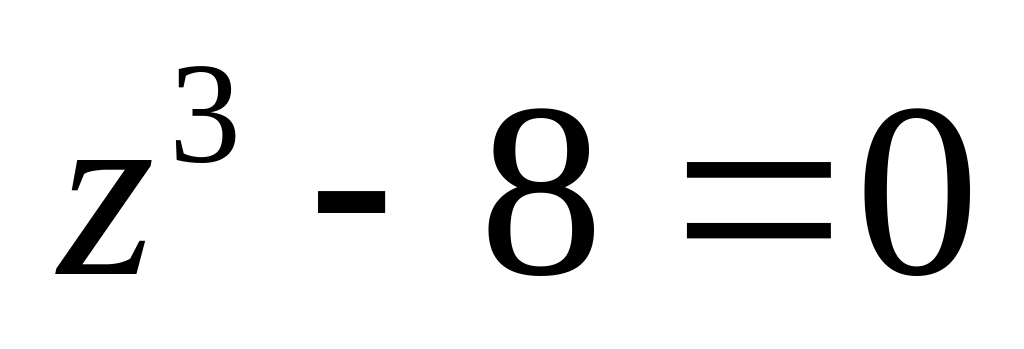 .
.Изобразить область, заданную неравенствами:
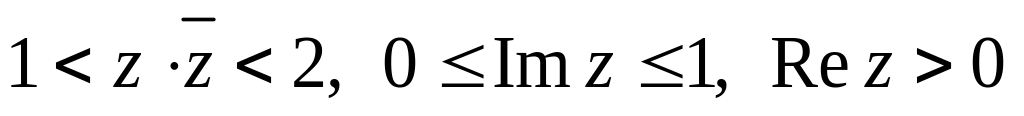 .
.
ВАРИАНТ 28
Даны комплексные числа:
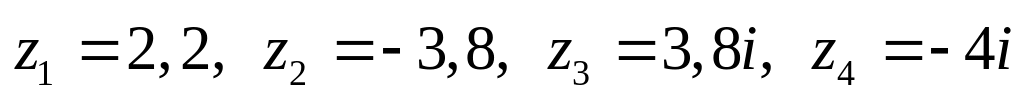 ,
,
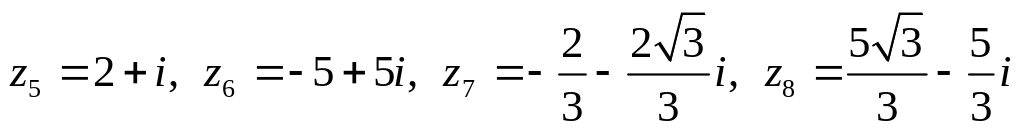 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
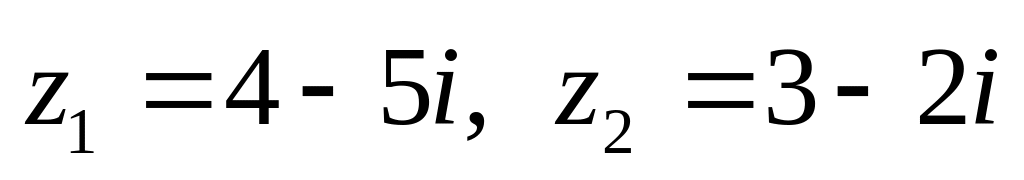 .
Вычислить
.
.
Вычислить
.Даны числа
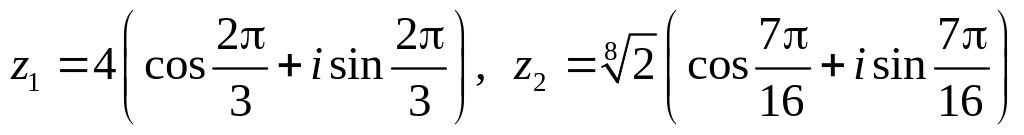 .
Вычислить
.
.
Вычислить
.Решить уравнение .
Изобразить область, заданную неравенствами:
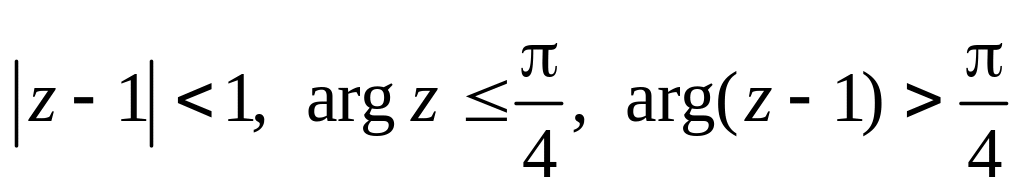 .
.
ВАРИАНТ 29
Даны комплексные числа:
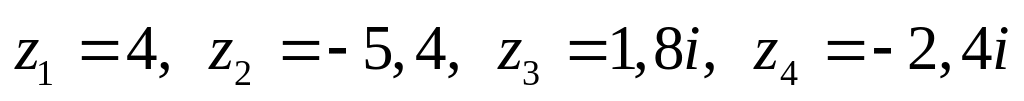 ,
,
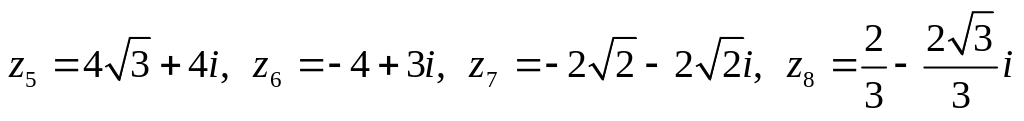 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
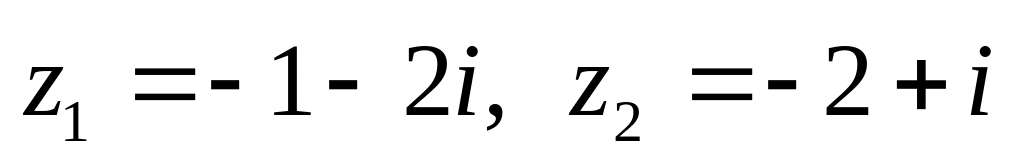 .
Вычислить
.
.
Вычислить
.Даны числа
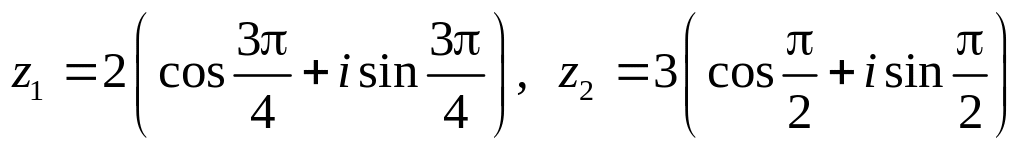 .
Вычислить
.
.
Вычислить
.Решить уравнение .
Изобразить область, заданную неравенствами:
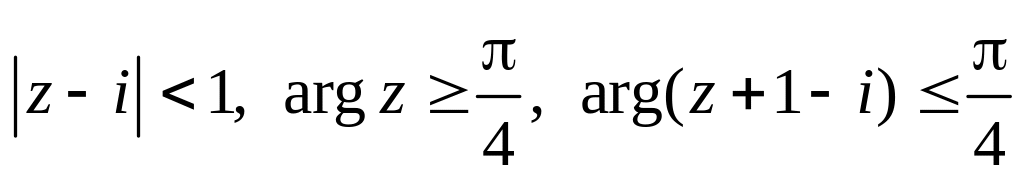 .
.
ВАРИАНТ 30
Даны комплексные числа:
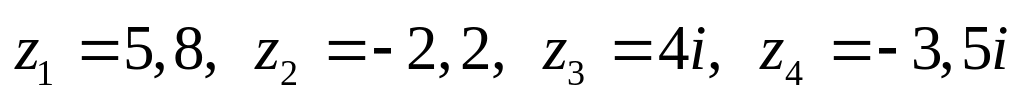 ,
,
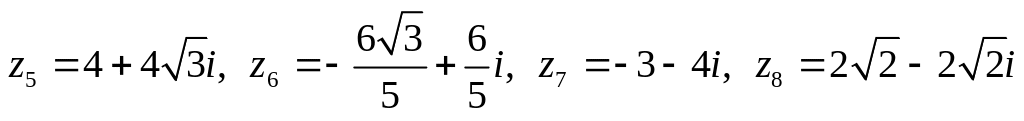 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
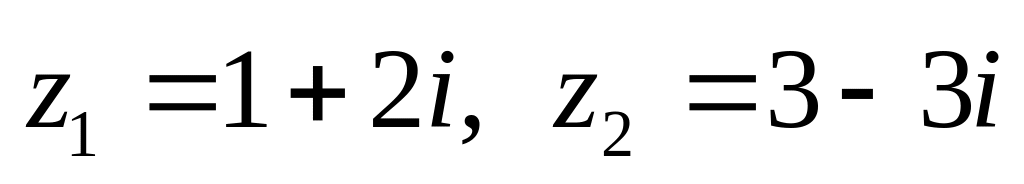 .
Вычислить
.
.
Вычислить
.Даны числа
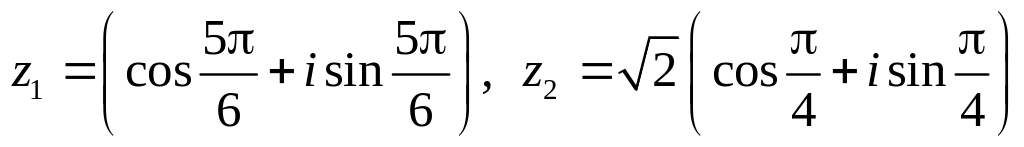 .
Вычислить
.
.
Вычислить
.Решить уравнение
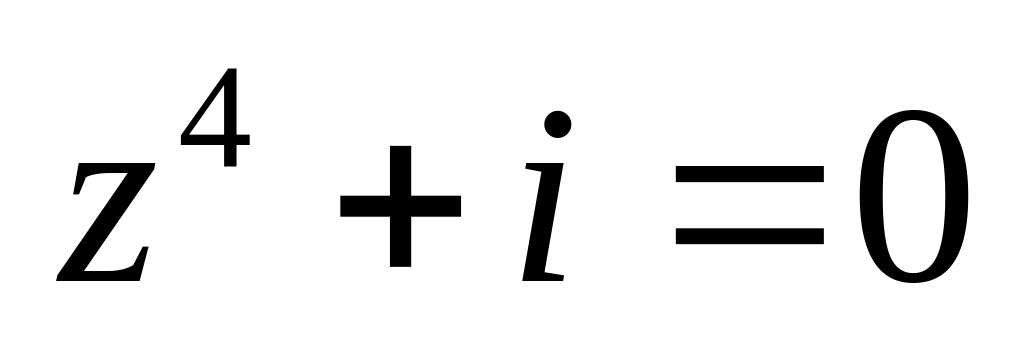 .
.Изобразить область, заданную неравенствами:
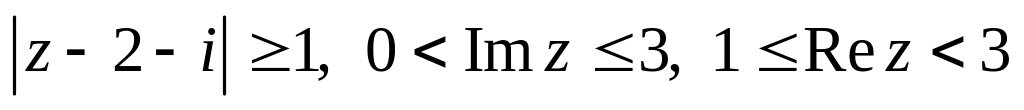 .
.
ВАРИАНТ 31
Даны комплексные числа:
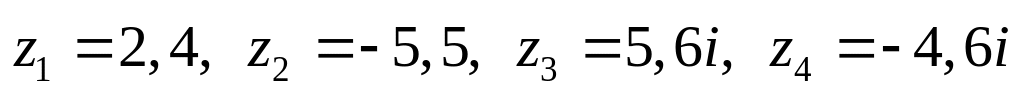 ,
,
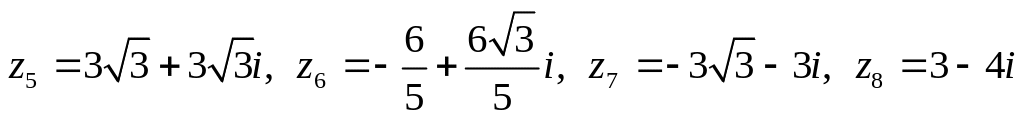 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
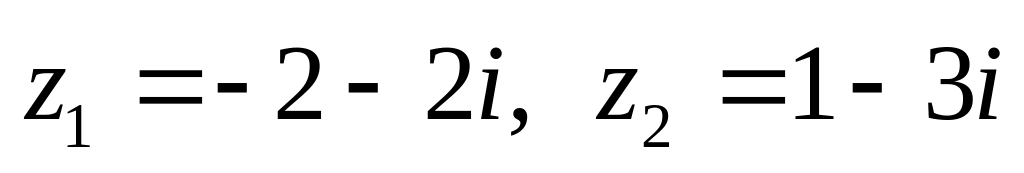 .
Вычислить
.
.
Вычислить
.Даны числа
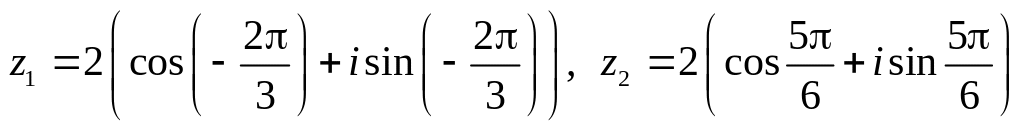 .
Вычислить
.
.
Вычислить
.Решить уравнение
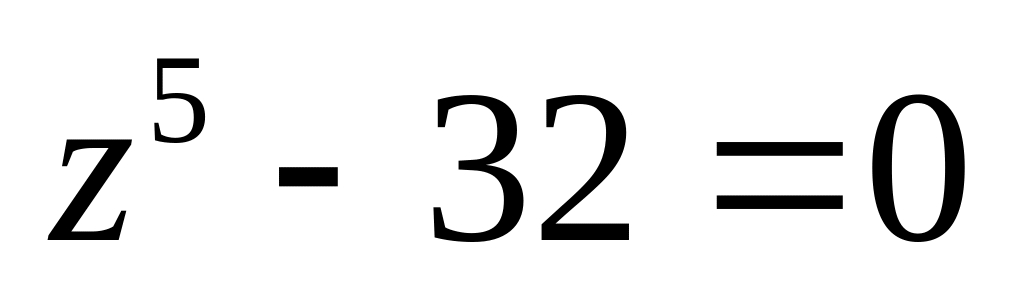 .
.Изобразить область, заданную неравенствами:
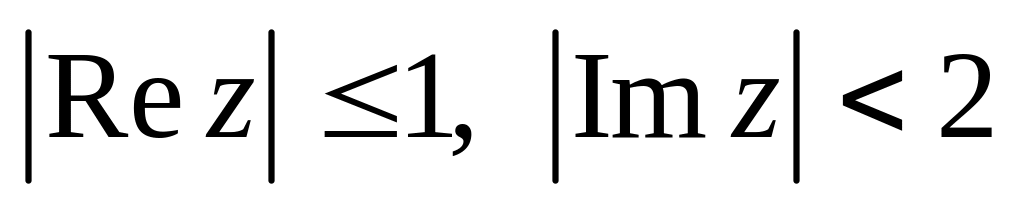 .
.
ВАРИАНТ 32
Даны комплексные числа:
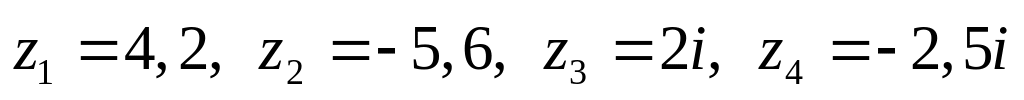 ,
,
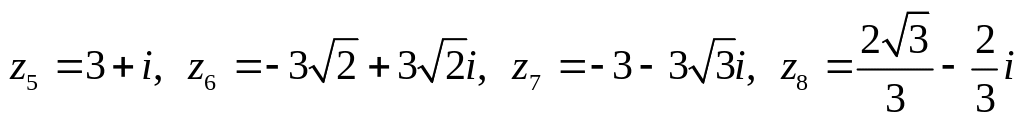 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
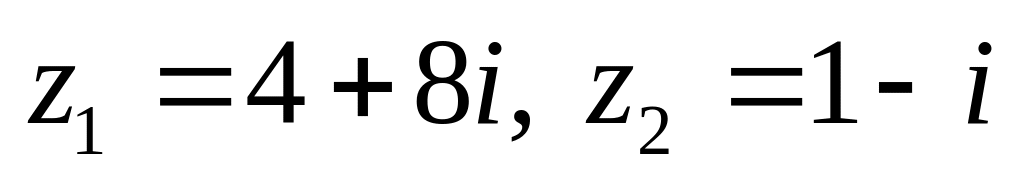 .
Вычислить
.
.
Вычислить
.Даны числа
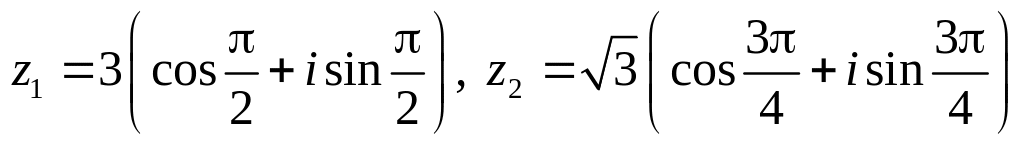 .
Вычислить
.
.
Вычислить
.Решить уравнение
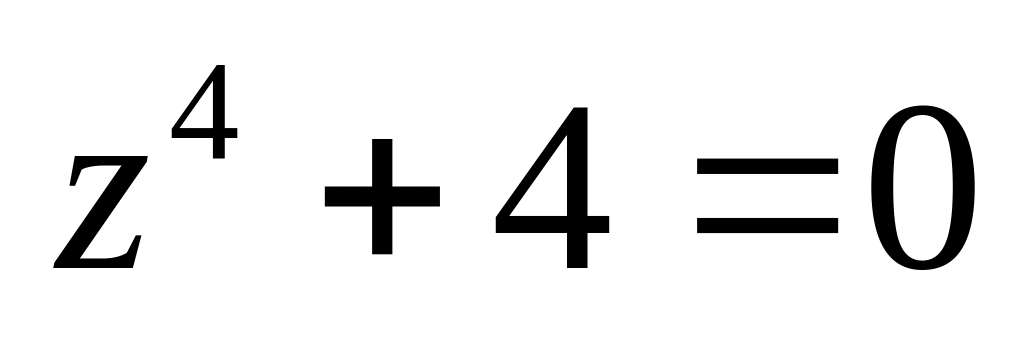 .
.Изобразить область, заданную неравенствами:
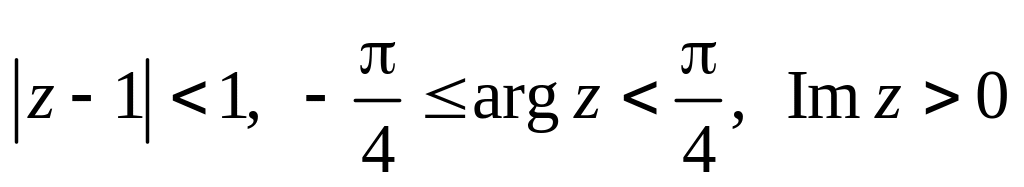 .
.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Краснов М. Л., Кисилев А. И., Макаренко Г. И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Учебное пособие. М., Наука, 1981.
Хапланов М. Г. Теория функций комплексного переменного. М., Просвещение, 1965.
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. М., Наука, ФИЗМАТЛИТ, 1999.
Привалов И. И. Введение в теорию функций комплексного переменного. М., Наука, 1984.
Сидоров Ю. В., Федорюк М. В., Шабунин М. И. Лекции по теории функций комплексного переменного. М., Наука, 1982.
Назаренко А. А., Прозоровская С. Д., Филиппова Т. И. Элементы теории функций комплексного переменного и операционное исчисление. Петродворец, ВВМУРЭ им. А.С.Попова, 1998.
Шостак Р. Я., Янпольский А. Р. Сборник задач по математике для втузов. Специальные разделы математического анализа. М., Наука, 1981.
Сборник задач по математике для втузов. Специальные разделы математического анализа (под редакцией А. В. Ефимова и Б. П. Демидовича). М., Наука, 1981.
Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч. II. М., Высшая школа, 1986.
