
Задача 5
Для построения области, заданной неравенствами, необходимо записать комплексное число z в алгебраической форме , затем построить на плоскости Оху области, соответствующие каждому неравенству, и найти их пересечение.
При построении области необходимо знать: определение модуля комплексного числа и формулу для его вычисления; определение аргумента комплексного числа, его геометрический смысл, определение комплексно-сопряженного числа; правило умножения двух комплексных чисел в алгебраической форме.
Пример
Изобразить
область, заданную неравенствами:
![]()
Решение
Запишем
,
тогда
![]() возведя левую и
правую части в квадрат, получим
возведя левую и
правую части в квадрат, получим
![]() Это открытая область – внешность круга,
радиуса равного 2, с центром в начале
координат. Граница области состоит из
окружности
Это открытая область – внешность круга,
радиуса равного 2, с центром в начале
координат. Граница области состоит из
окружности
![]() .
.
Неравенство
![]() означает, что мы должны рассмотреть
только 1-ю четверть (включая оси Ох
и Оу).
означает, что мы должны рассмотреть
только 1-ю четверть (включая оси Ох
и Оу).
Итак,
неравенства
![]() означают внешность круга
означают внешность круга
![]() расположенную в 1-й четверти (рис. 4).
расположенную в 1-й четверти (рис. 4).




 у
у




0 2 х
Рис. 4.
Индивидуальные задания
ВАРИАНТ 1
Даны комплексные числа:
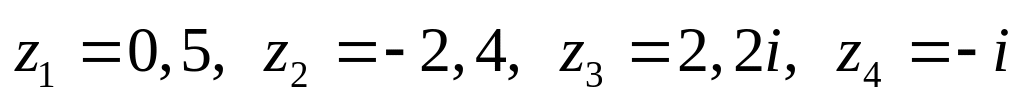 ,
,
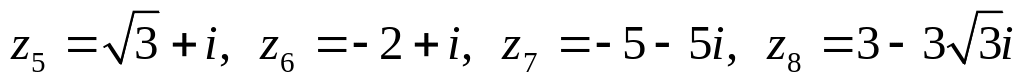 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
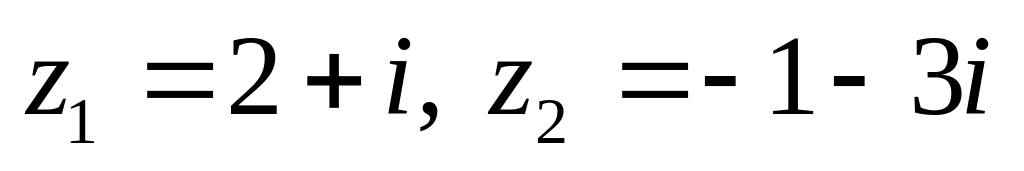 .
Вычислить
.
Вычислить
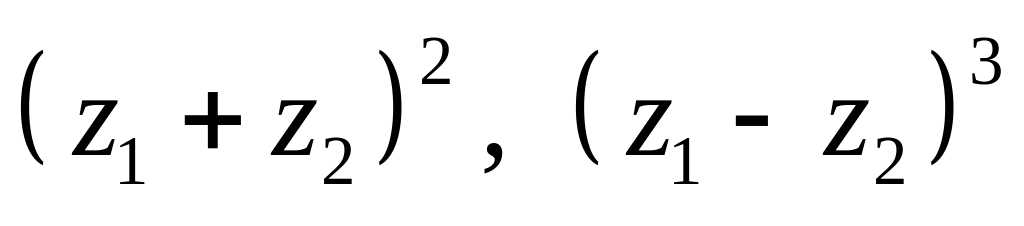 .
.Даны числа
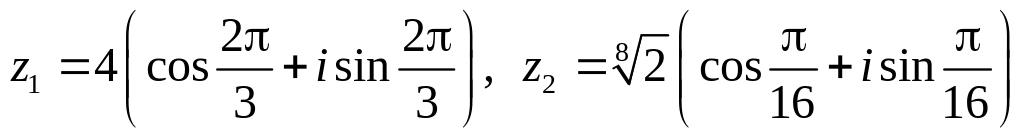 .
Вычислить
.
.
Вычислить
.Решить уравнение
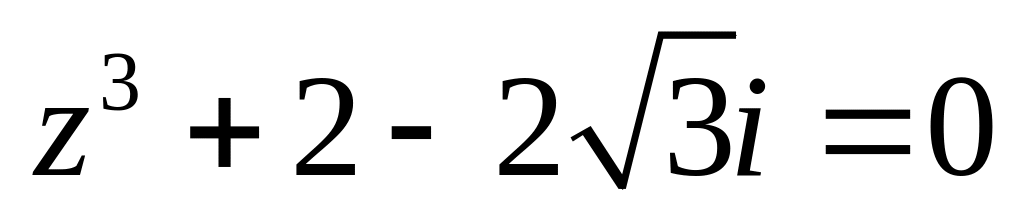 .
.Изобразить область, заданную неравенствами:
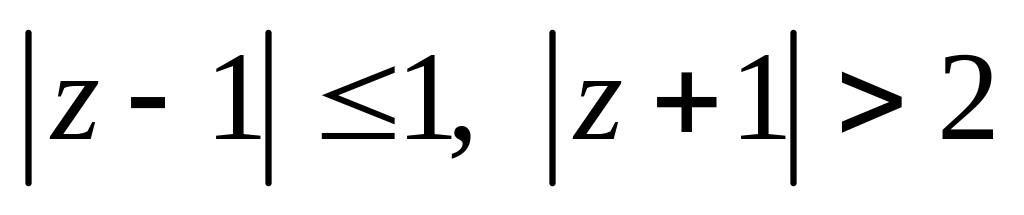 .
.
ВАРИАНТ 2
Даны комплексные числа:
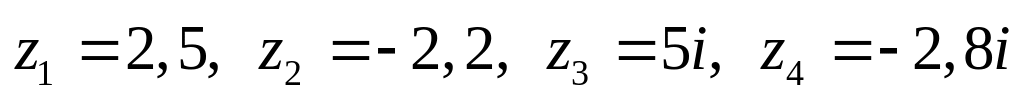 ,
,
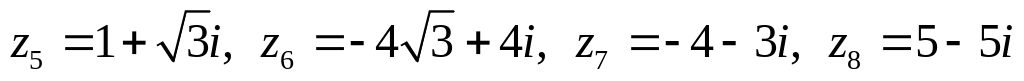 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
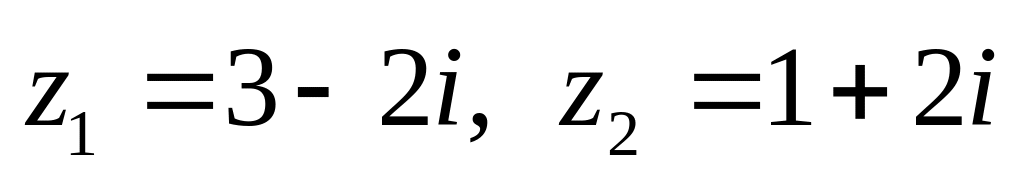 .
Вычислить
.
.
Вычислить
.Даны числа
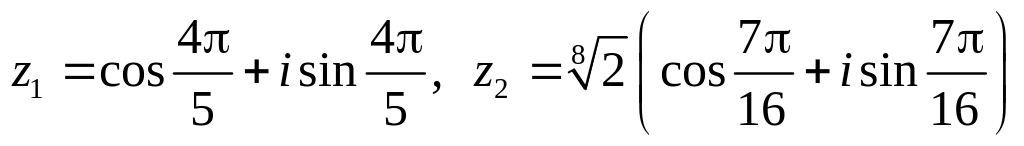 .
Вычислить
.
.
Вычислить
.Решить уравнение
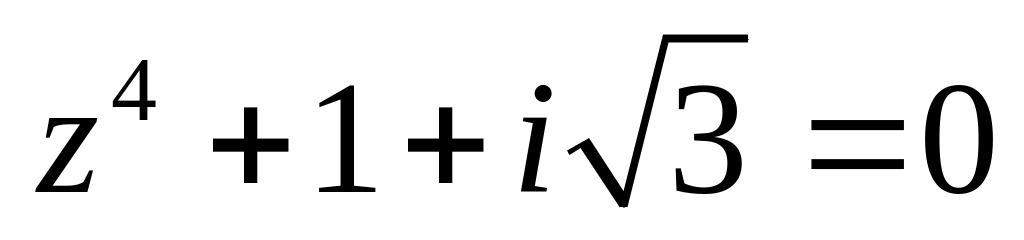 .
.Изобразить область, заданную неравенствами:
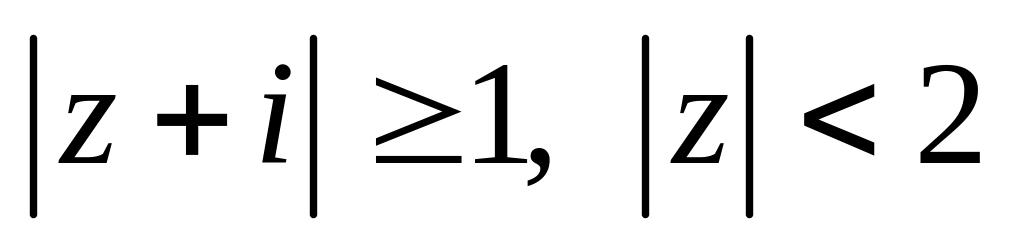 .
.
ВАРИАНТ 3
Даны комплексные числа:
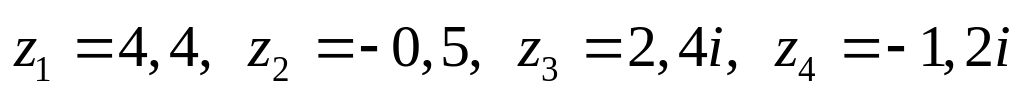 ,
,
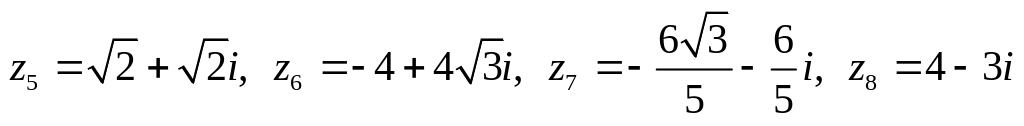 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
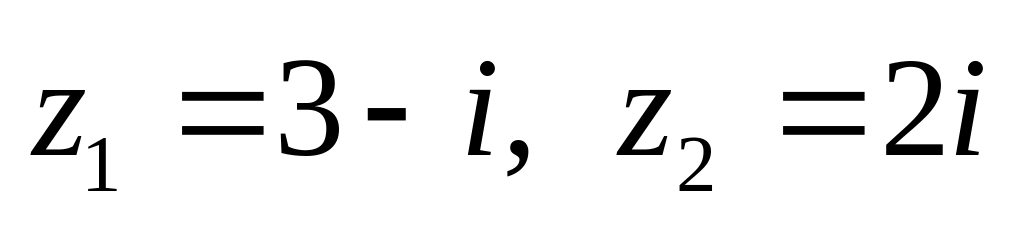 .
Вычислить
.
.
Вычислить
.Даны числа
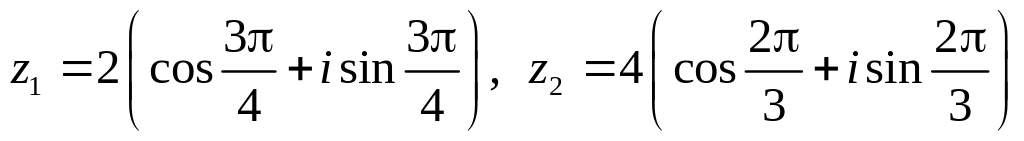 .
Вычислить
.
.
Вычислить
.Решить уравнение
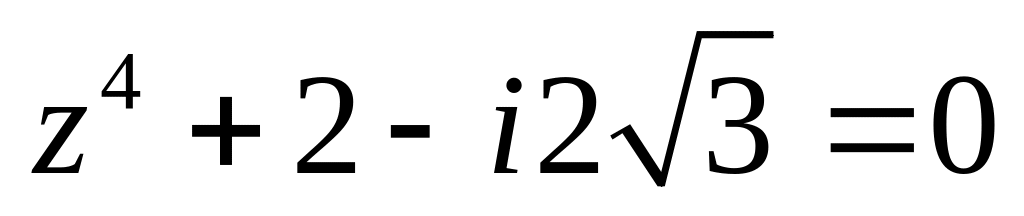 .
.Изобразить область, заданную неравенствами:
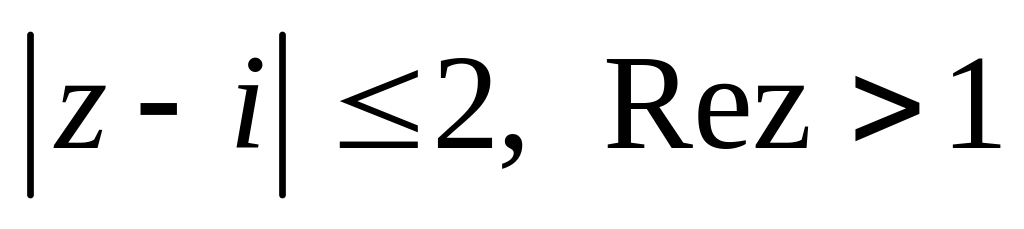 .
.
ВАРИАНТ 4
Даны комплексные числа:
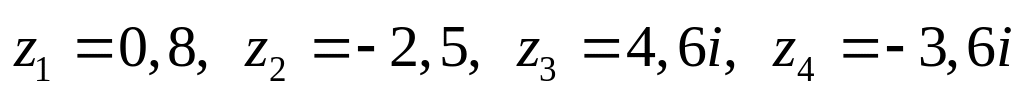 ,
,
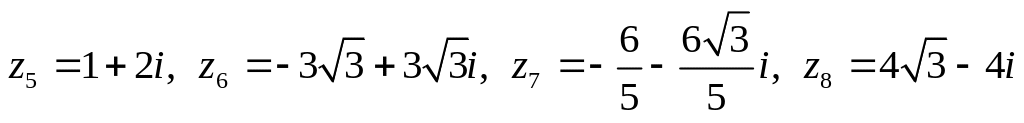 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
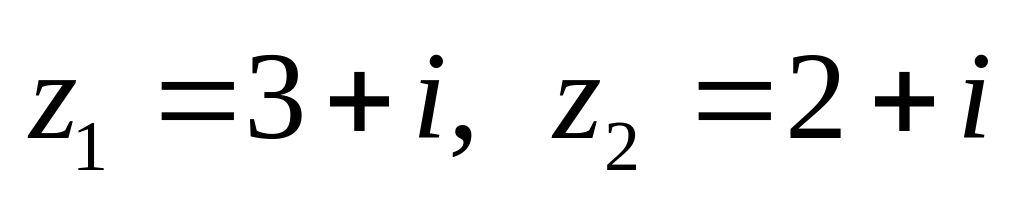 .
Вычислить
.
.
Вычислить
.Даны числа
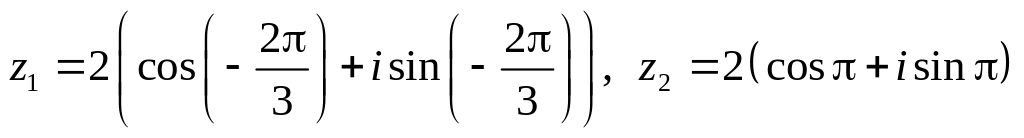 .
Вычислить
.
.
Вычислить
.Решить уравнение
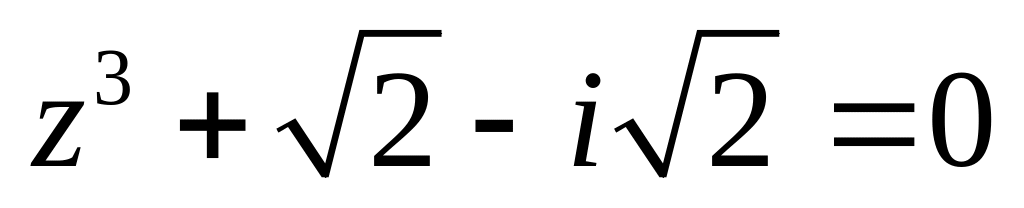 .
.Изобразить область, заданную неравенствами:
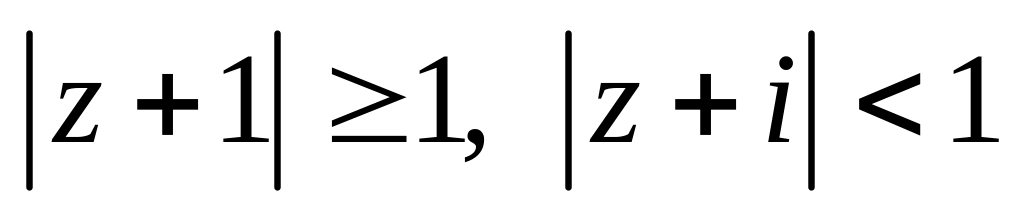 .
.
Вариант 5
Даны комплексные числа:
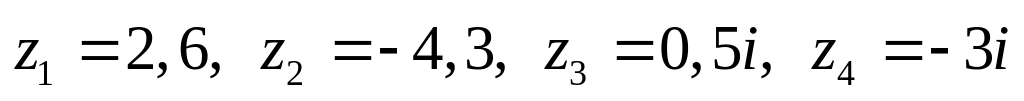 ,
,
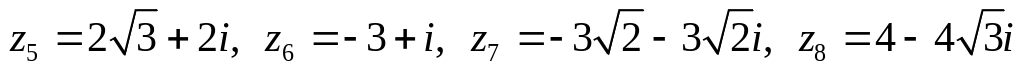 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
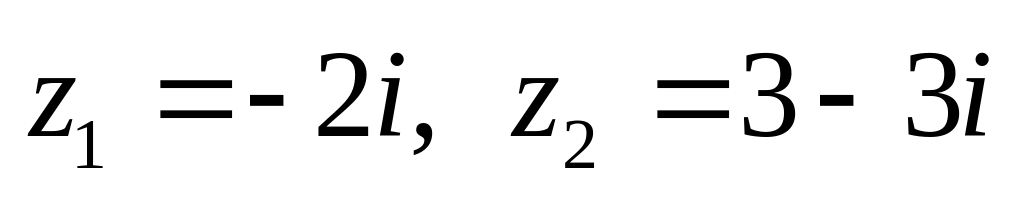 .
Вычислить
.
.
Вычислить
.Даны числа
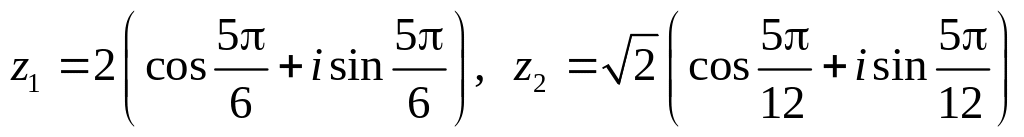 .
Вычислить
.
.
Вычислить
.Решить уравнение
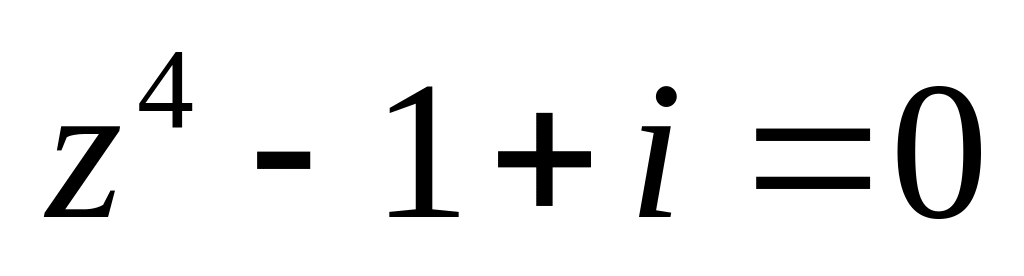 .
.Изобразить область, заданную неравенствами:
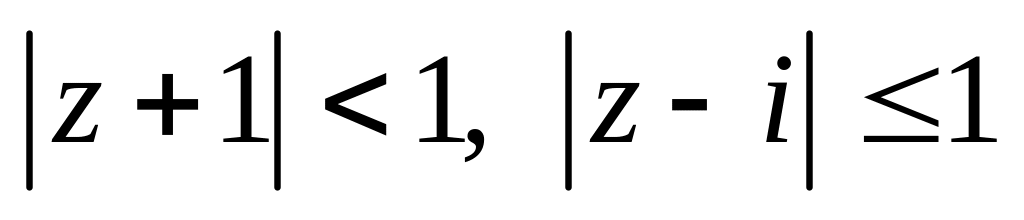 .
.
ВАРИАНТ 6
Даны комплексные числа:
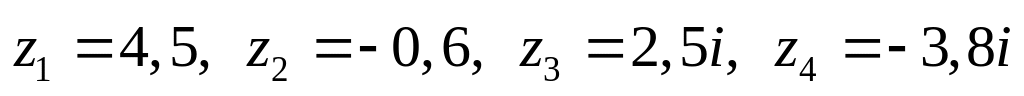 ,
,
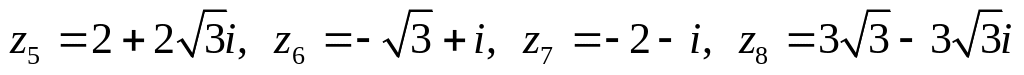 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
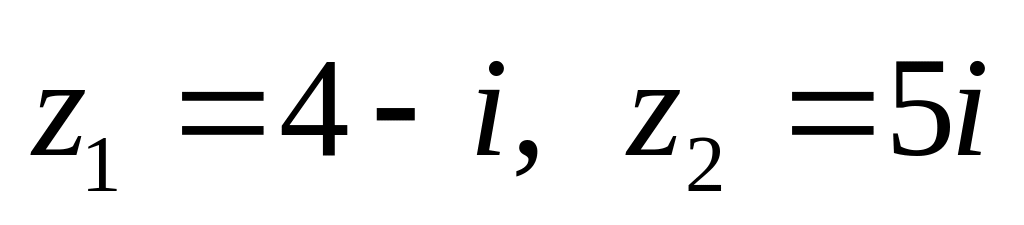 .
Вычислить
.
.
Вычислить
.Даны числа
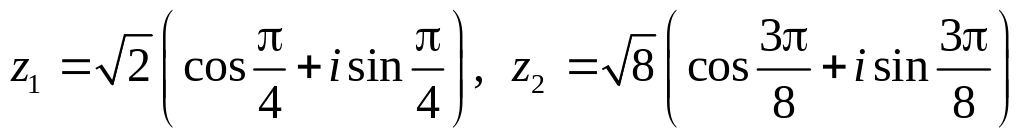 .
Вычислить
.
.
Вычислить
.Решить уравнение
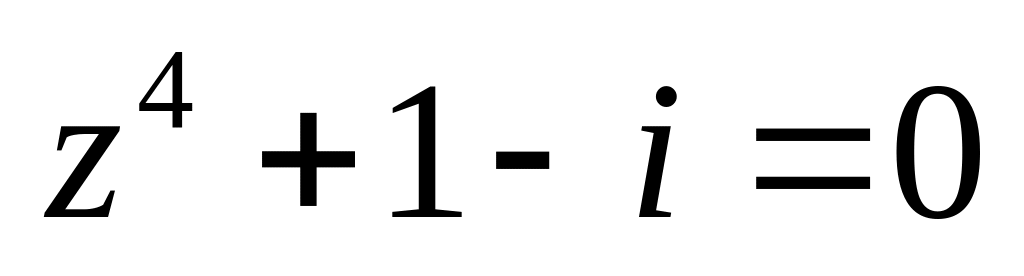 .
.Изобразить область, заданную неравенствами:
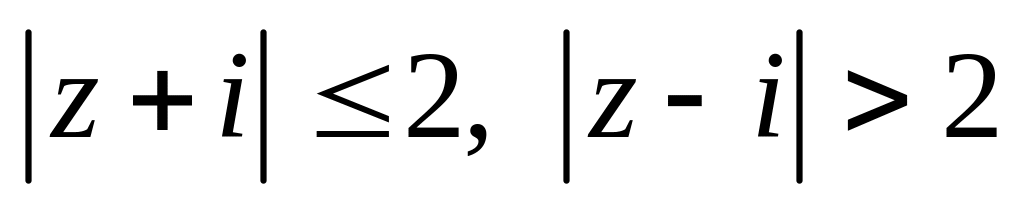 .
.
ВАРИАНТ 7
Даны комплексные числа:
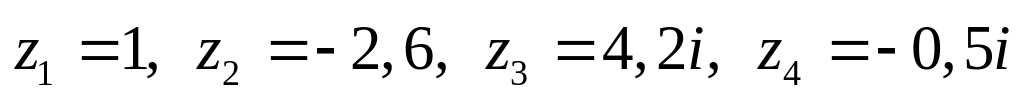 ,
,
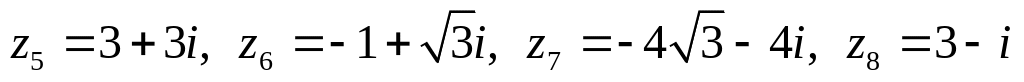 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
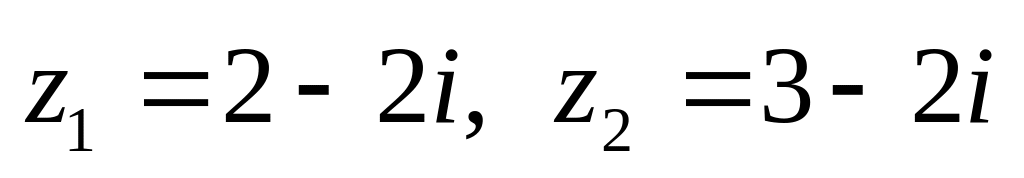 .
Вычислить
.
.
Вычислить
.Даны числа
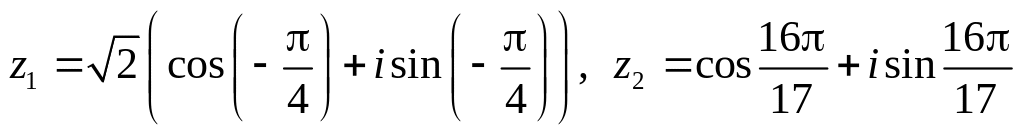 .
Вычислить
.
.
Вычислить
.Решить уравнение
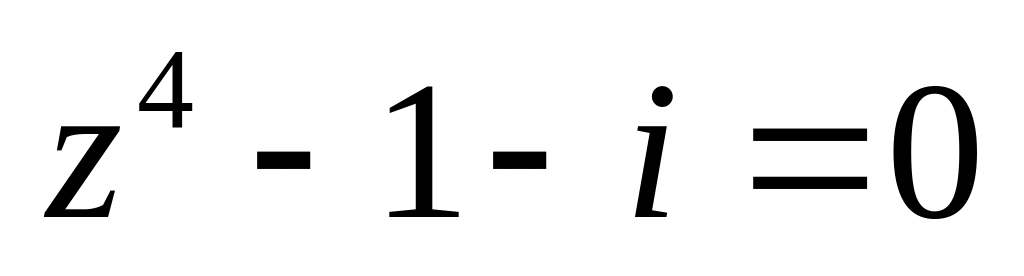 .
.Изобразить область, заданную неравенствами:
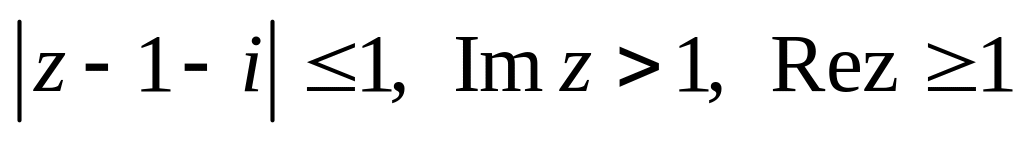 .
.
ВАРИАНТ 8
Даны комплексные числа:
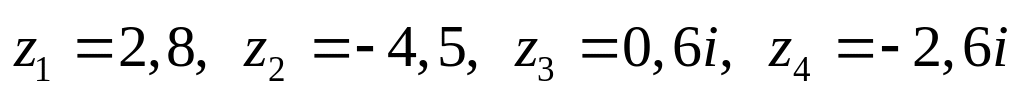 ,
,
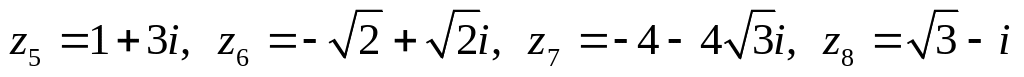 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
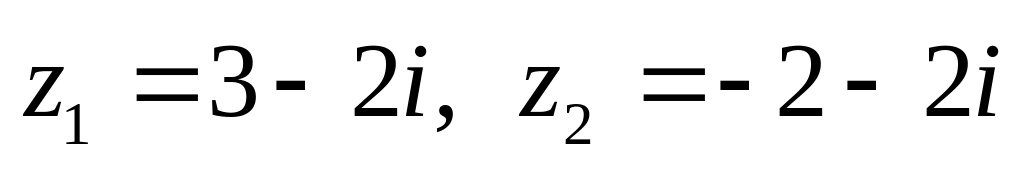 .
Вычислить
.
.
Вычислить
.Даны числа
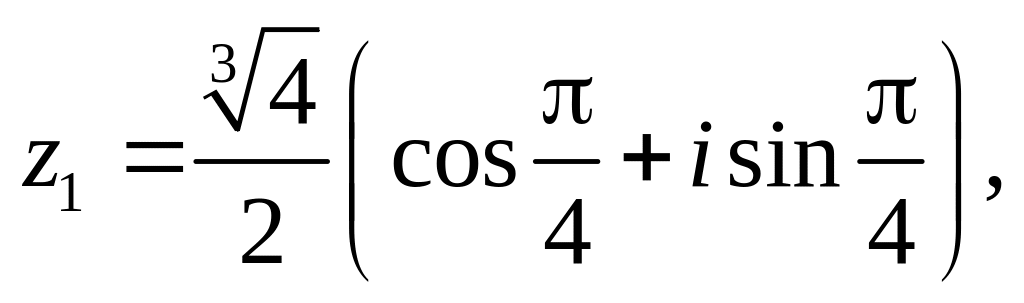
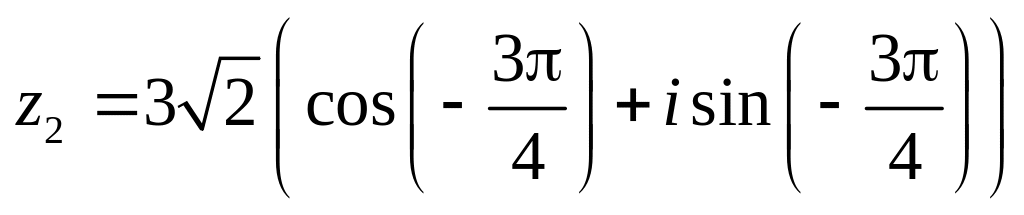 .
Вычислить
.
.
Вычислить
.Решить уравнение
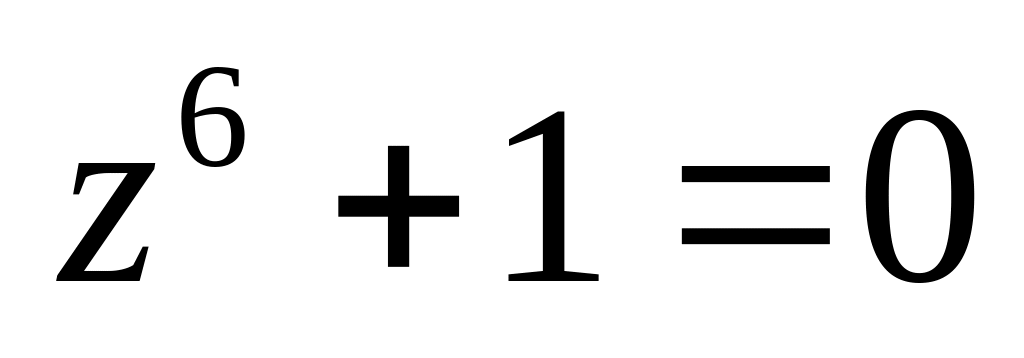 .
.Изобразить область, заданную неравенствами:
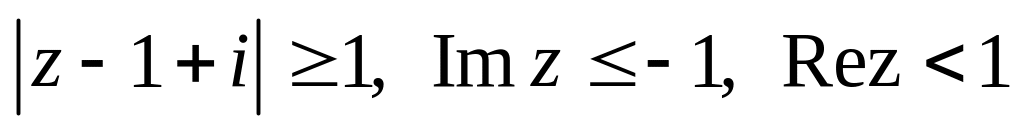 .
.
ВАРИАНТ 9
Даны комплексные числа:
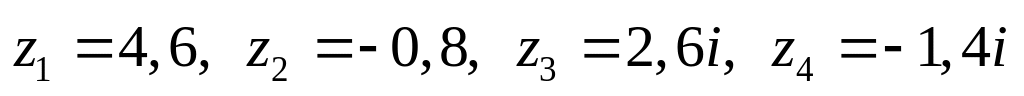 ,
,
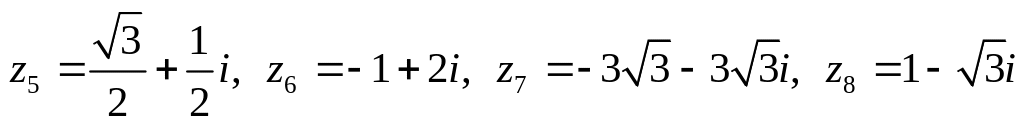 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
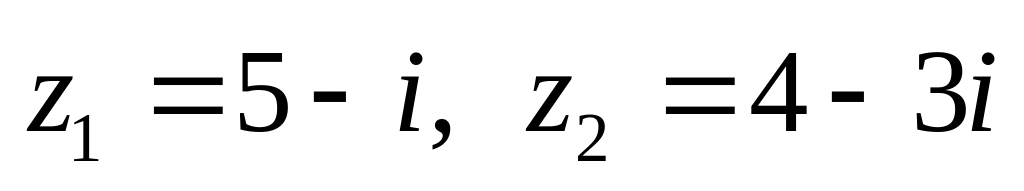 .
Вычислить
.
.
Вычислить
.Даны числа
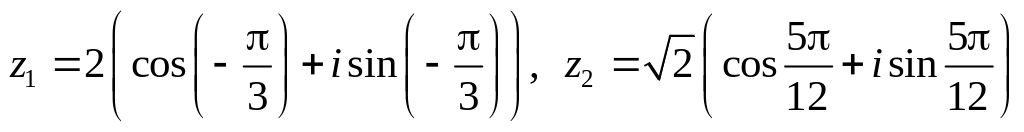 .
Вычислить
.
.
Вычислить
.Решить уравнение
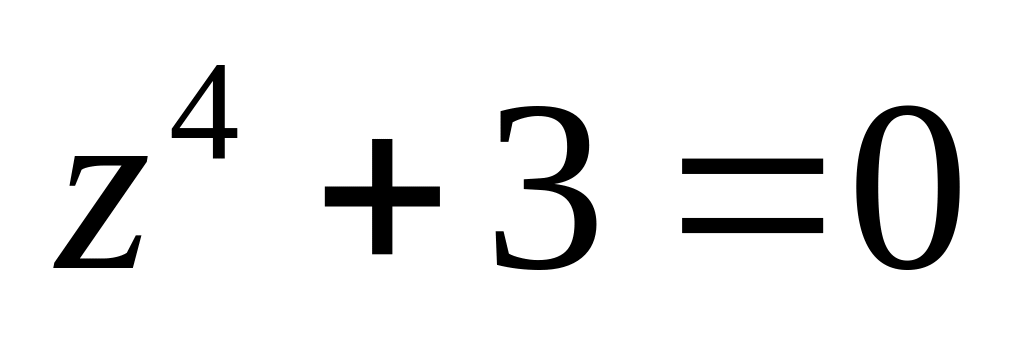 .
.Изобразить область, заданную неравенствами:
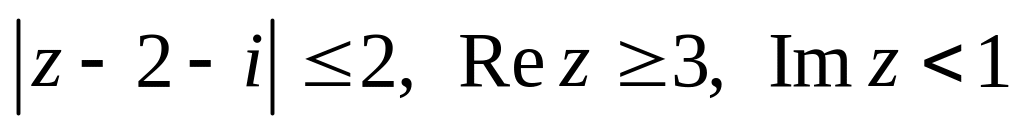 .
.
ВАРИАНТ 10
Даны комплексные числа:
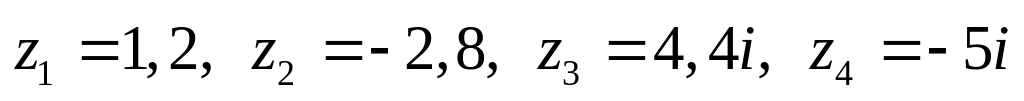 ,
,
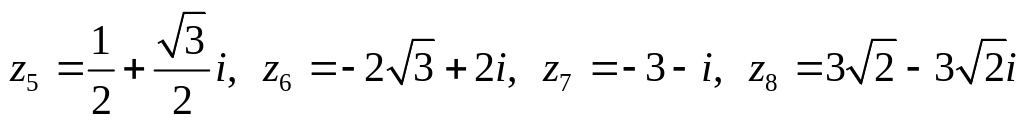 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
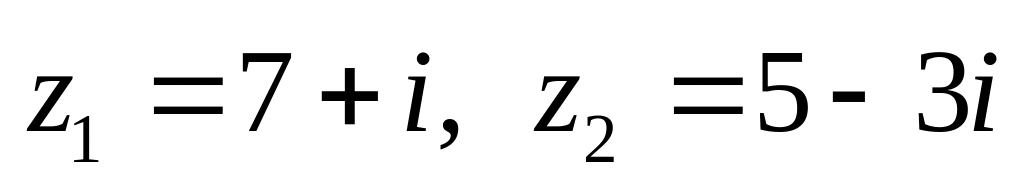 .
Вычислить
.
.
Вычислить
.Даны числа
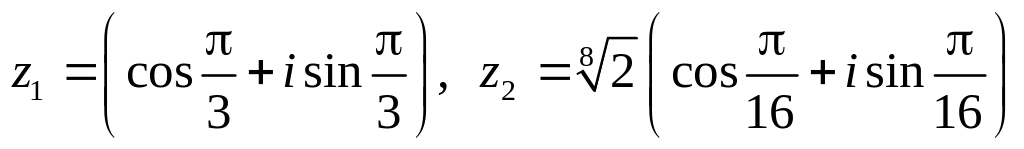 .
Вычислить
.
.
Вычислить
.Решить уравнение
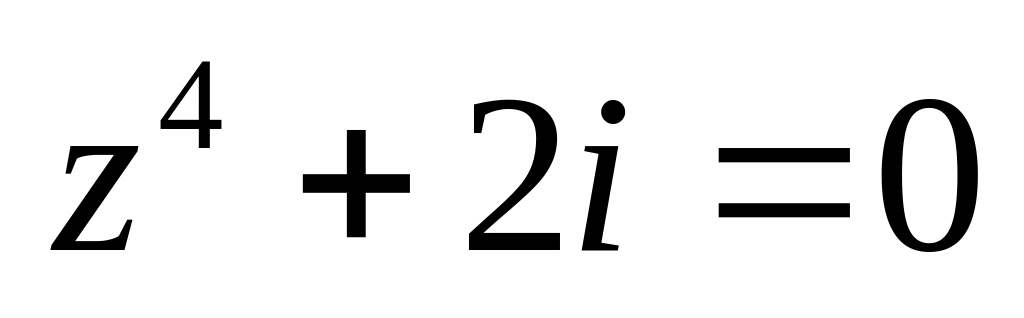 .
.Изобразить область, заданную неравенствами:
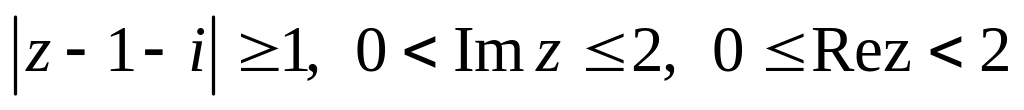 .
.
ВАРИАНТ 11
Даны комплексные числа:
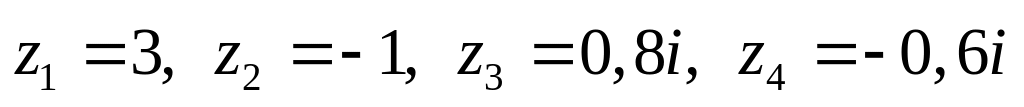 ,
,
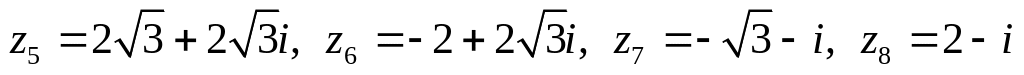 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
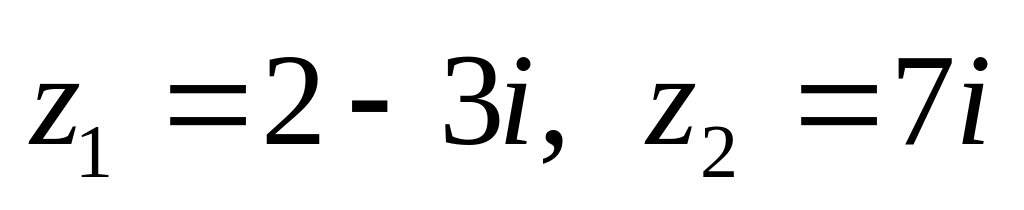 .
Вычислить
.
.
Вычислить
.Даны числа
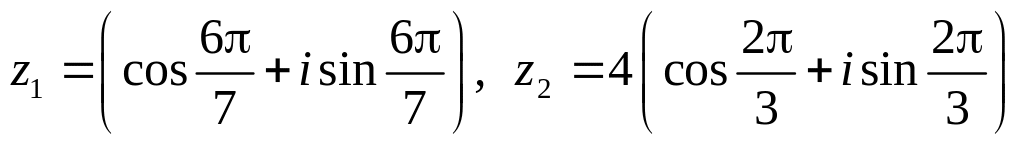 .
Вычислить
.
.
Вычислить
.Решить уравнение
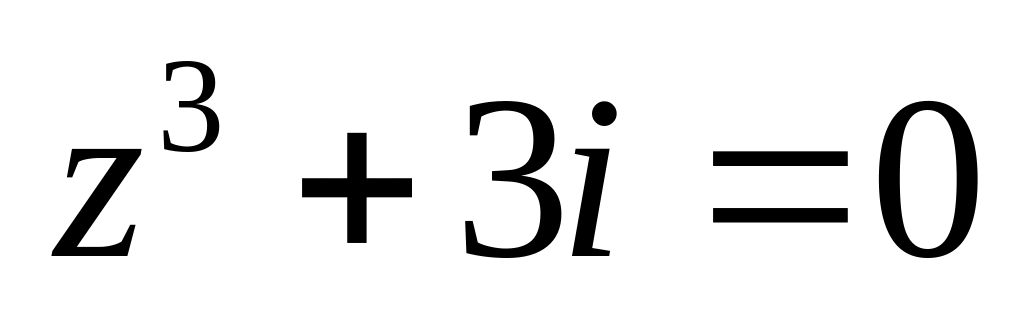 .
.Изобразить область, заданную неравенствами:
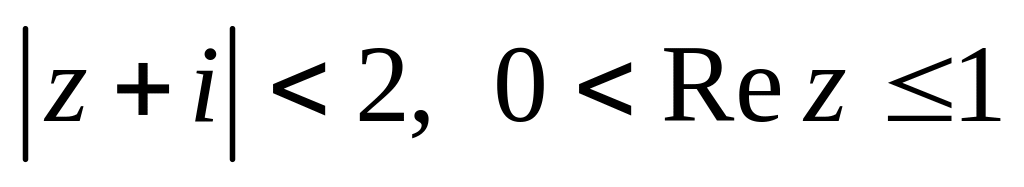 .
.
ВАРИАНТ 12
Даны комплексные числа:
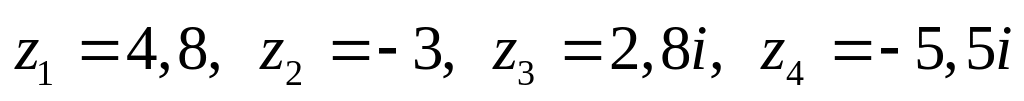 ,
,
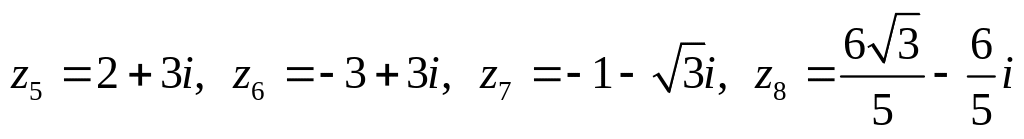 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
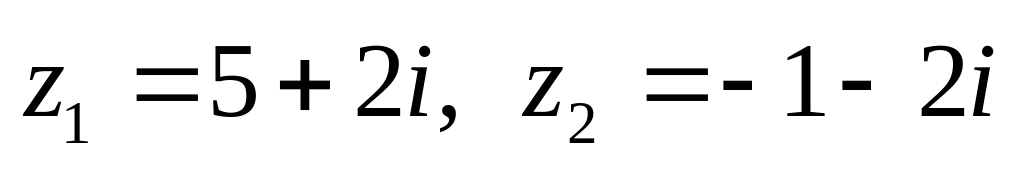 .
Вычислить
.
.
Вычислить
.Даны числа
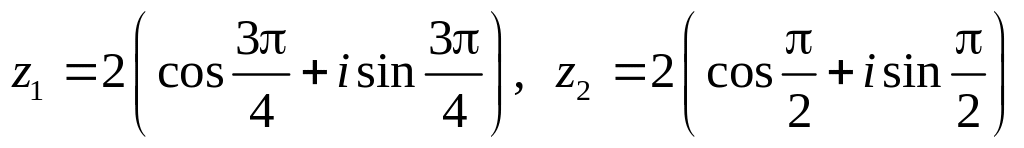 .
Вычислить
.
.
Вычислить
.Решить уравнение
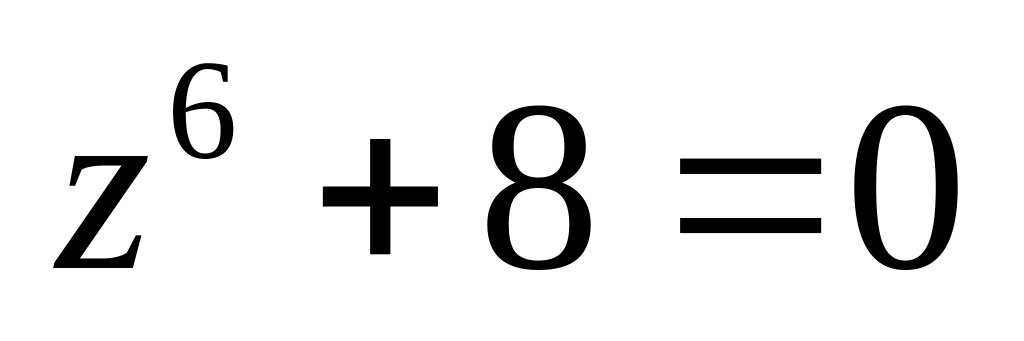 .
.Изобразить область, заданную неравенствами:
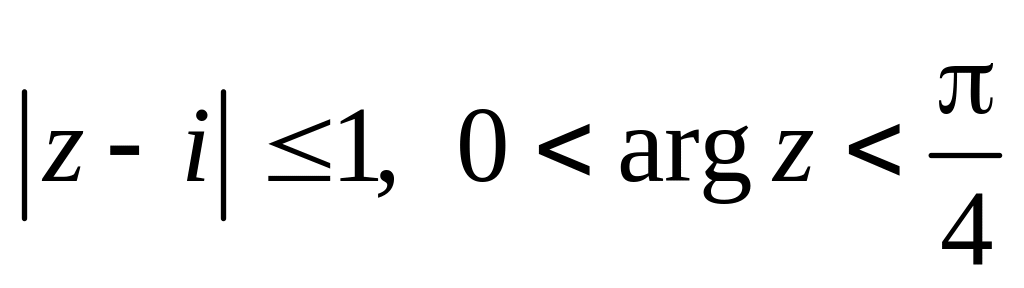 .
.
ВАРИАНТ 13
Даны комплексные числа:
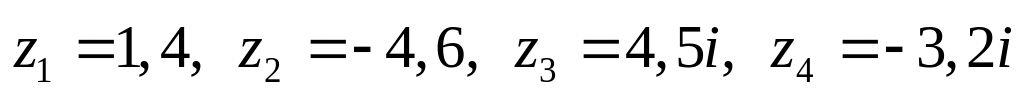 ,
,
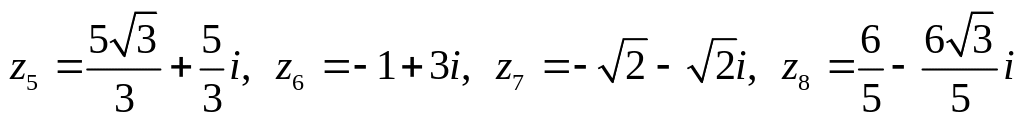 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
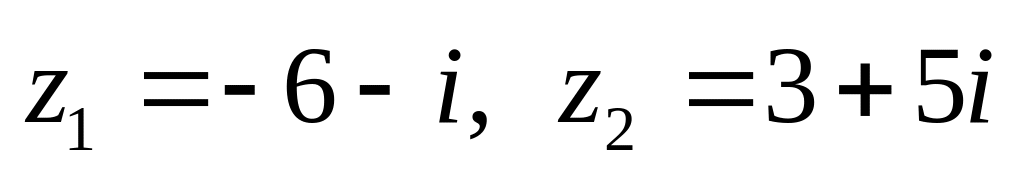 .
Вычислить
.
.
Вычислить
.Даны числа
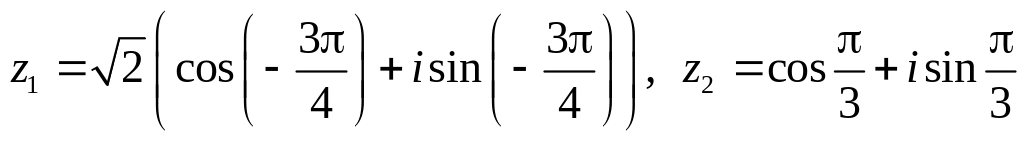 .
Вычислить
.
.
Вычислить
.Решить уравнение
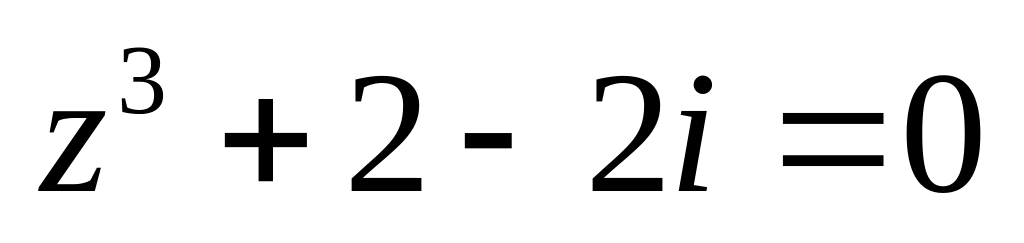 .
.Изобразить область, заданную неравенствами:
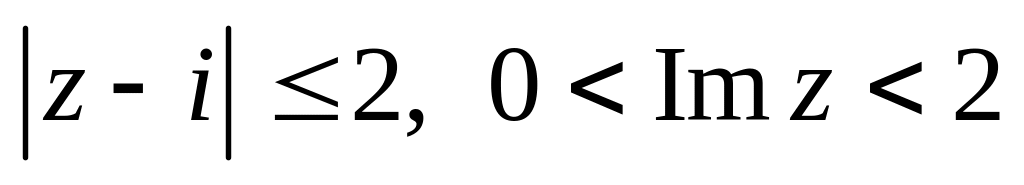 .
.
ВАРИАНТ 14
Даны комплексные числа:
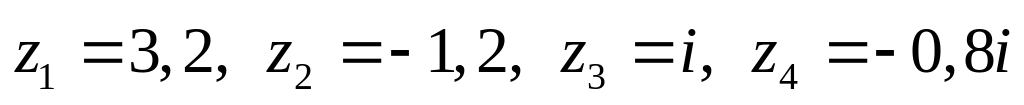 ,
,
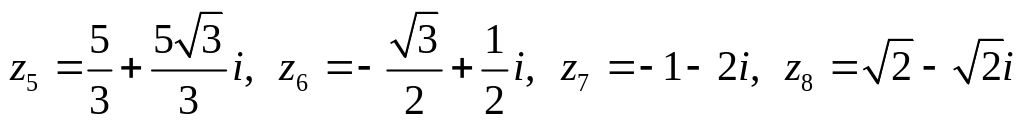 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
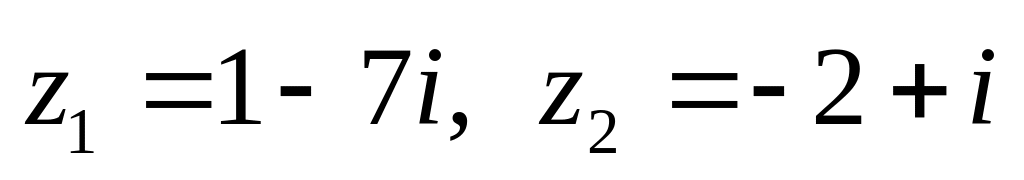 .
Вычислить
.
.
Вычислить
.Даны числа
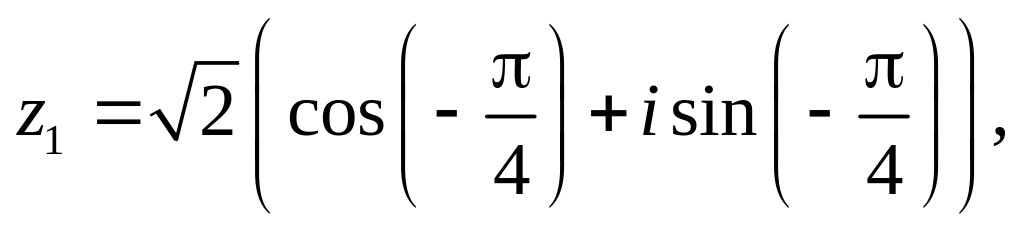
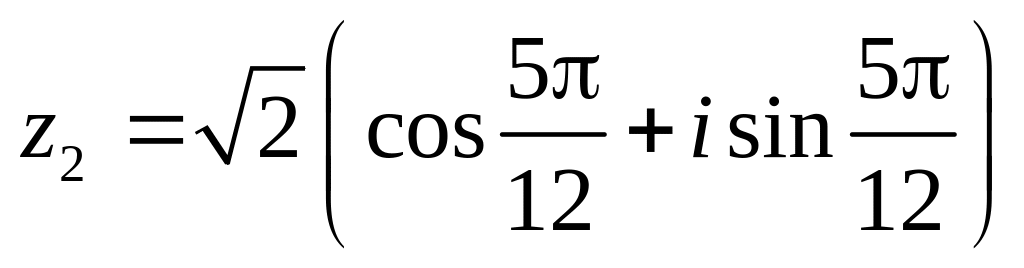 .
Вычислить
.
.
Вычислить
.Решить уравнение
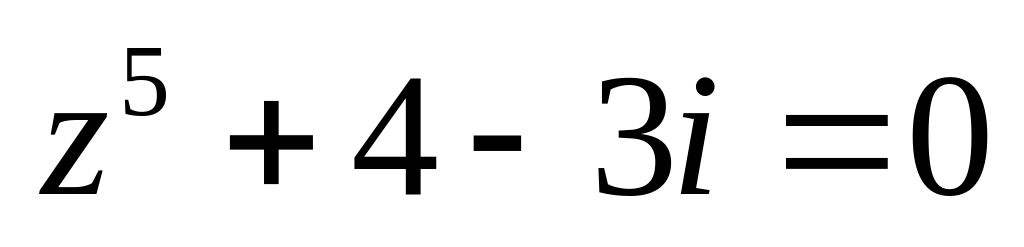 .
.Изобразить область, заданную неравенствами:
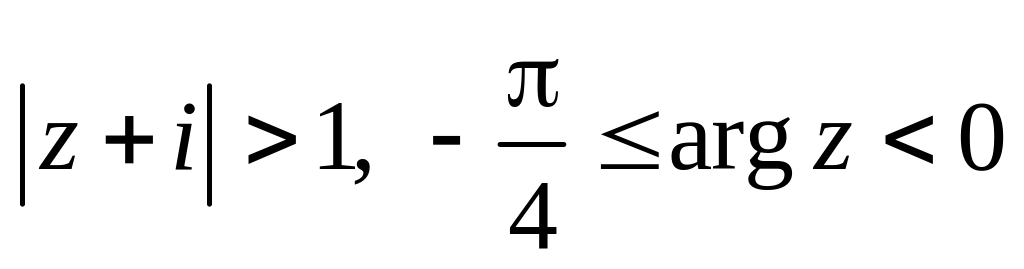 .
.
ВАРИАНТ 15
Даны комплексные числа:
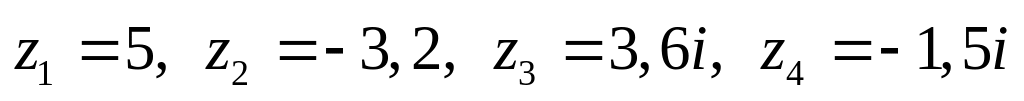 ,
,
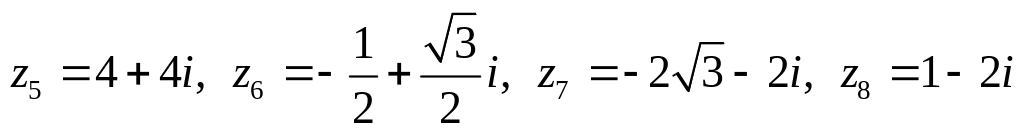 .
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.
.
Изобразить числа на комплексной
плоскости, найти модуль и аргумент,
записать в тригонометрической и
показательной форме.Даны числа
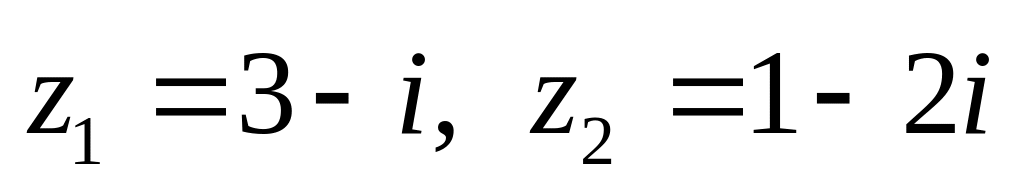 .
Вычислить
.
.
Вычислить
.Даны числа
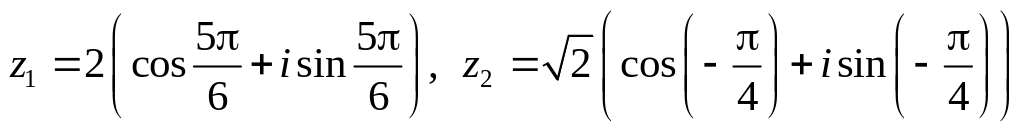 .
Вычислить
.
.
Вычислить
.Решить уравнение
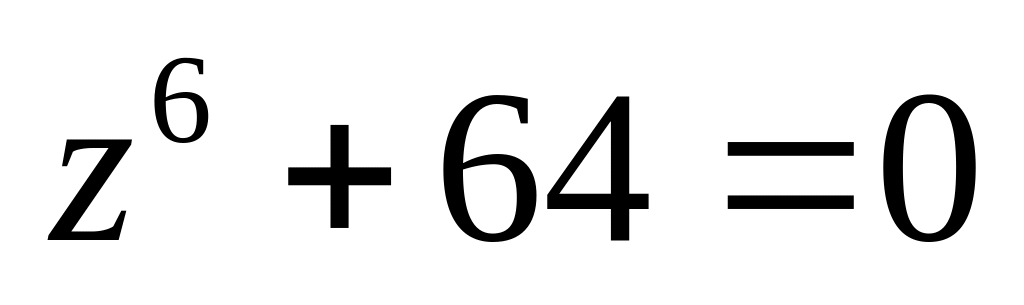 .
.Изобразить область, заданную неравенствами:
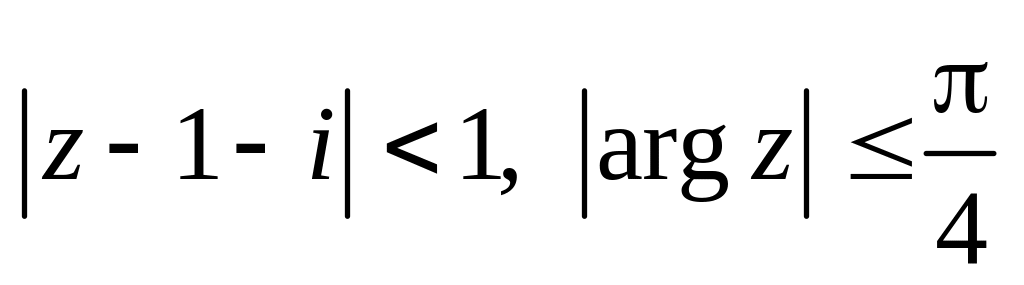 .
.
