1. Вычислить пределы функций

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1
2
3
4

2. Найти области определения функций и построить их на плоскости

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1
2
3
4
5
6

Порядок проведения занятия:

1. Получить допуск к работе

2. Выполнить задания

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется функцией двух переменных?

2. Дать определение предела функции двух переменных. Как вычислить предел функции двух переменных?

3. Что является областью определения функции двух переменных?

ПРИЛОЖЕНИЕ

Понятие функции нескольких переменных

Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных

z = f(x, y)

Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Окрестностью точки М₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .

Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа  > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие , также верно и условие .

Записывают:

Пример 1. Вычислить предел

Решение. Воспользуемся повторным пределом функции двух переменных. Получим:

Пример 2. Найти область определения функции и изобразить ее на плоскости.

Решение. Данная функция имеет действительные значения, если . Этому неравенству удовлетворяют все точки I и IV четверти. Область существования функции выглядит следующим образом:

Пример 3. Найти область существования функции

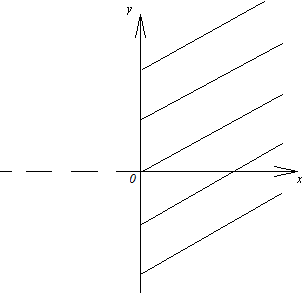
Решение. Функция имеет действительные значения, если или . Последнему неравенству удовлетворяют координаты точек, лежащих внутри окружности радиуса 2 с центром в начале координат. Область существования функции есть внутренность этого круга.