Задача об измерении параметров вибрационных процессов ставится следующим образом. На вход аппаратуры поступает измеряемая величина Х_вх(t),рассматриваемая как сигнал. Это могут быть смещение линейное или угловое исследуемого компонента вибрации, его производные по времени или интегралы.

С выхода аппаратуры снимается отклик Х_вых(t).

Преобразователь (линейка)

система

сигнал отклик

Х_вх(t) Х_вых(t)

Преобразователь при этом рассматривается как единая физическая система и чтобы отклик Х_вых(t) правильно отображал сигнал Х_вх(t) преобразователя.

При динамических измерениях Х_вх(t) представляет собой величину, изменяющуюся во времени. Заданная функциональная зависимость по возможности не должна искажаться измерительным устройством, т.е. для идеального прибора должно соблюдаться соотношение

Х_вых(t) = К Х_вх(t) (1.1) или Х_вых(t - τ) = К Х_вх(t) (1.2), где К = const.

В соотношении (1.2) допускается запаздывание отклика на время τ. Другими словами, отклик и сигнал должны иметь одинаковую форму.

Эти требования в общем случае не выполняется, так как наличие масс и пружин в механических приборах и индуктивностей и емкостей в электроизмерительных устройствах приводит к более сложным связям между входной Х_вх(t) и выходной Х_вых(t) величинами, а именно к связям, описываемым посредством дифференциального уравнения вместо простого алгебраического уравнения.

Для описания работы измерительного прибора в динамическом режиме, прежде всего необходимо выделить и рассмотреть те характеристики, которые определяют этот режим, а затем исследовать вопрос о влияние их на качество измерения.

Будем считать измерительную систему линейной; это значит, что ее статическая амплитудная характеристика должна быть линейно возрастающей ( или по меньшей мере с хорошим приближением аппроксимироваться возрастающей прямой в своей рабочей части), а параметры накопителей энергии и показатель затухания ( масса подвижной части, упругость пружин, емкости и индуктивности в электрической схеме, а также величины сопротивлений и коэффициенты демпфирования) должны быть постоянными, не зависящими от изменений входной величины.

Дифференциальное уравнение.

Предположив, что система линейна, можно описать ее поведение в динамическом режиме посредством линейного дифференциального уравнения с постоянными коэффициентами.

A_nХ_выхⁿ + A_n-1Х_вых^{n -1} +…+ A₂Х_вых^̎+ A₁Х_вых^̍ +A₀Х_вых=

= В₀ Х_вх+ В₁ Х_вх^̍ + В₂Х_вх^̎ +… + В_m Х_вх^m (1.3), где

Верхние индексы Х_вх иХ_вых означают операции дифференцирования по времени.

Если система представляет собой измерительную цепь, состоящую из нескольких звеньев ( преобразователь, усилитель, показывающий прибор и т.д. ), то она описывается соответственно системой взаимосвязанных линейных дифференциальных уравнений.

Х_вх (удар, взрыв, импульс,вынуждающая сила и т.д.)

Х_вых – одна из обобщенных координат, движение которой измеряется (амплитуда, скорость, ускорение и т.д.)

В простейшем случае дифференциальное уравнение можеи иметь следующий вид (1.4), (1.5):

a₀Х_выхⁿ+ a₁Х_вых^{n -1} +…+ a_nХ_вых = f(t) = Х_вх(t) (1.4)

или

+ a_n Х_вых = f(t) = Х_вх(t) (1.5)

Воздействия бывают детерминированные и случайные.

Для случайных процессов используется аппарат теории случайных функций. Из теории дифференциальных уравнений известно, что решение уравнения (1.4) состоит из общего решения однородного уравнения (1.6) и частного решения неоднородного уравнения.

a₀dⁿ /dtⁿх_вых+ a₁dt^n-1/dt^n-1x_вых + a_n-1d/dtx_вых+ a_nx_вых = 0 (1.6)

Х_вых(t) = X_общ + Х_ч(1.7)

Таким образом, при действии входного воздействия (вынуждающей силы) система участвует в двух движениях: собственное движение системы и вынужденное движение системы под действием вынуждающей силы (правой части уравнения).

Пример, при действии вынуждающей силы f(t) на систему с одной степенью свободы (рис. 1)

Уравнение движения запишется в виде:

x̎_вых+ 2nx̍ +ω₀²x = F(t)/m (1.8) , где 2n = ℒ/m, ω₀² = c/m (1.9),при условии что, корни характеристического уравнения

р² + 2np + ω₀² = 0 (1.10) равны p_1,2 = -n±jω₁, ω₁ = при <

Общее решение однородного уравнения

x̎_вых+ 2nx̍ +ω₀²x =0 (1.11)

запишется: X_общ = ₁sin ₁t + ₂ cos ₁t)

Частное решение неоднородного уравнения при F(t) = Asin tбудет иметь вид

X _ч = A/c 1/ ω²/ω₀⁴sin ( ωt +φ) (1.12) , где

φ= arctg -2n/ω₀² – ω²(1.13)

Решения уравнения (7) при имеем виду

(1.14)

Константы находятся из начальных условий

, (1.15)

Из (14) и (15) следует, что при любых начальных условиях (в том числе и нулевых) в системе будут возникать собственные и движения системы с частотой и вынуждающие движения системы с частотой вынуждающий силы .

Если входное воздействие

(1.16)

в системе будут возникать собственные колебания системы и вынуждающие колебания системы.

Причем, каждая амплитуда отклика каждой гармоники будет преобразовываться в соответствие с соотношениями (12,14). В отклике 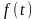соотношение между амплитудами будет искажено, будут возникать амплитудно-частотные искажения и, кроме того, все гармоники отклика будут сдвинуты друг относительно друга на некоторый угол (будут возникать фазово-частотные искажения).

Так как входное воздействие может быть произвольным, в том числе и импульсом (ударное воздействие), а импульс можно представить в виде ряда (14), будут возникать серьёзные проблемы определения входного воздействия по отклику из-за возникновения амплитудно-частотных и фазово-частотных искажений.

Кроме того, первое слагаемое в соотношении(2) представляющие собственное движение системы, искажает амплитуду отклика. Лишь, когда закончат собственные затухающие колебания системы, можно приступить к измерению параметров отклика (проблемы определения параметров быстропротекающих процессов).

Таким образом, при определении параметров вынуждающей силы будут возникать статические и динамические искажения входного воздействия.

Статические искажения связаны с нелинейностью статической характеристики.

Динамические искажения связаны с возникновением амплитудно-

И фазово- искажений.

Кроме того , при измерении быстропротекающих процессов переходит процесс должен быть достаточно быстрым, чтобы измерить параметры входного воздействия.

Точно определить по отклику параметры выступающей силы можно только с некоторой точностью….

Современный анализ вибрационных процессов основан на применении выходных преобразований Лапласа и Фурье к анализу вибрационных процессов.

Применение этих преобразований в рассмотрении протекающих процессов не во временной области, а на комплексной плоскости или в частотной области. При этом , если система описывает линейным дифференциальным уравнением с постоянными коэффициентами .

Математическое представление, состоящие из членов вида :

реальным физическим разложением на гармонические составляющие, представляющими ряда (интеграла). При этом каждая гармоническая составляющая данной проходит через преобразования.

При применении преобразований Лапласа и Фурье можно сформулировать специфические требования к измерительной системе, и кроме того , анализ системы в частотной области позволяет оптимальную измерительную систему с экспериментальными исследованиями каждого элемента (преобразованием), входящего в систему.

Основными

-понятия АЧХ и ФИХ

-применение специальных функций, позволяющих о быстродействии измерительной системы

-возможности экспериментальной измерительных систем

Преобразования Лапласа и Фурье и их приложение к интегрированию систем линейных дифференциальных уравнений с постоянными коэффициентами

2.1. Общее представление о преобразовании Лапласа

Пусть задана функция f(t), равная нулю при t<0 и отличная от нуля при всех или хотя бы некоторых значениях t 0. Тогда интегралом Лапласа функции f(t) называется интеграл вида

(2.2.1)

где p - комплексное число.

Обозначим этот интеграл L[f(t)]=f(p)

Если f(t) задана, то для каждого значения числа р можно подсчитать значение

L[f(t)]. В каждом смысле L[f(t)] есть функция р. Каждой f(t) при некоторых общих ограничениях, накладываемых на нее, соответствует определенная функция L[f(t)]=f(p).

Функция f(t) называется оригиналом, а функция L[f(t)]- преобразованием Лапласа или изображением функции f(t). Запишем это так:

f(p)= L[f(t)]÷ f(t) (2.2.2)

Определение изображения по оригиналу составляет прямую задачу теории преобразования Лапласа. Определение оригинала по изображению составляет обратную задачу теории преобразования Лапласа.

Для теории автоматического регулирования наиболее существенно, что применение преобразования Лапласа позволяет сильно упростить интегрирование систем линейный дифференциальных уравнений с постоянными коэффициентами.

3⁰. Определение изображения от определенного интеграла.

Если

L[f(t)]=f(p)÷f(t) (2.2.3)

То

L[ (2.2.4)

4⁰. Изображения основных функций, встречающихся в задачах регулирования. В таблице П.1 приведены изображения Лапласа для некоторых функций, встречающихся в задачах теории регулирования.

Таблица П.1

Оригинал	Изображение
L[const I]
L[tn I]
L[I sin
L[cos
L[I sin(
L[I cos(
L[I sh at]=L[I (
L[I ch at]=L[I ( + )]
L[I ]
L{I t[ M cos sin t]}

Выражения эти легко проверить подстановкой соответствующих f(t) в интеграл, определяющий преобразование Лапласа и непосредственным интегрированием.

Выше всюду I обозначает функцию t, равную 0 при t<0 и равную 1 при t 0 («единичная функция»).

5⁰. Построение изображения функции с запаздывающим аргументом. Если

L[f(t)]=f(p) f(t)

то

L[f(t)] f(t- ) (2.2.5)

где .

6⁰. Построение оригинала для произведения изображений двух функций. Пусть

L[f₁(t)] f₁(t) и L[f₂(t)] f₂(t)

Тогда

L[f₁(t)]L[f₂(t)] ₁(t- )f₂( )d =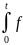 ₁( )f₂(t- )d (2.2.6)

Интеграл такого вида называется сверткой двух функций.

Произведению двух изображений будет соответствовать не произведение оригиналов, а их свертка.

7⁰. Предельные свойства преобразований Лапласа. Обозначим F(p)=L[f(t)] f(t), и пусть все плюсы F(p) имеют отрицательную действительную часть. Тогда

[f(t)]_t=0=[pF(p)]_p= (2.2.7)

и наоборот,

[f(t)]_t= =[pF(p)]_p=0 (2.2.8)

т.е. предельные значения функции f(t) можно найти, подставив в ее изображение , умноженное на p, значение p=0 или p= . Этими формулами можно воспользоваться, чтобы определить предельные значения решения дифференциального уравнения по виду этого уравнения, не решая его.