Задача 6. Розрахунок стержнів на стійкість Теоретична довідка
1. Для гнучких центрально стиснутих стержнів крім розрахунку на міцність слід виконувати також розрахунок на стійкість .
2. Критична сила Fкр - це осьова стискувальна сила, від дії якої стержень переходить у стан байдужої рівноваги ( стан рівноваги, коли після малого відхилення стержня від початкової прямолінійної форми рівноваги він залишається в новому положенні рівноваги).
3. Величину критичної сили
Fкр
і критичного напруження
для стержнів великої
гнучкості визначають
за формулами Ейлера:
;
,
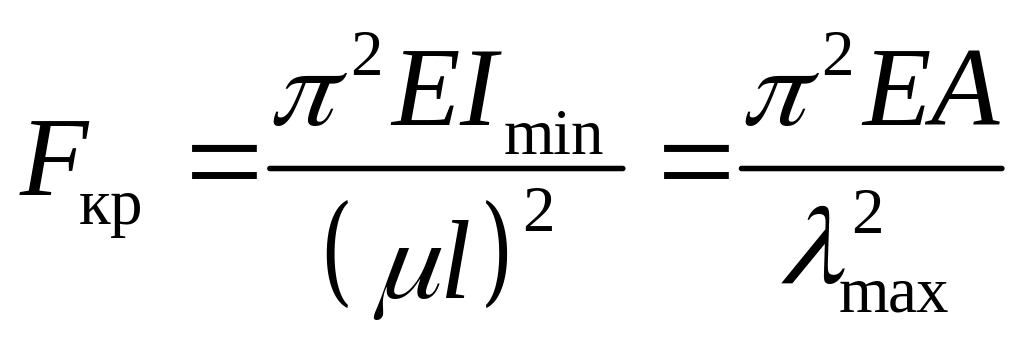де Е -
модуль Юнга матеріалу; A
, Imin
- відповідно площа та мінімальний
момент інерції поперечного перерізу;
- коефіцієнт, що залежить від способу
закріплення стержня (деякі зі способів
закріплення стержня та значення
коефіцієнтів
показані на рис. 16); l
- довжина стержня;
- максимальна гнучкість
стержня;
- мінімальний радіус
інерції поперечного
перерізу стержня.
Рис. 16
Формули для визначення Imin та а деяких перерізів
Прямокутник
;
;
(якщо α=1, дістаємо
квадратний переріз).
Кільце
;
;
(якщо
дістаємо круглий переріз).
Пустотілий квадрат
;
;
(якщо
дістаємо квадрат).
Прокатні профілі (двотавр, швелер) величини Imin=Iy та A вибирають з таблиць сортаменту.
4. Сталеві стержні вважають
стержнями великої
гнучкості, якщо
.
Якщо
,
то стержні є стержнями
середньої гнучкості,
для яких критичне напруження визначають
за формулою Ясінського
,
де для сталі а= 31 кН/см2; b = 0,114 кН/см2.
5. Умова стійкості стиснутого стержня має вигляд
,
звідси допустима сила
,
де
- коефіцієнт, який вибирають з таблиці
залежно від матеріалу стержня та
гнучкості стержня
.
Таблиця коефіцієнтів
Гнучкість
|
(сталь) |
(дерево) |
Гнучкість |
(сталь) |
(дерево |
0 |
1,00 |
1,00 |
110 |
0,52 |
0,25 |
10 |
0,99 |
0,99 |
120 |
0,45 |
0,22 |
20 |
0,96 |
0,95 |
130 |
0,40 |
0,18 |
30 |
0,94 |
0,93 |
140 |
0,36 |
0,16 |
40 |
0,92 |
0,87 |
150 |
0,32 |
0,14 |
50 |
0,89 |
0,80 |
160 |
0,29 |
0,12 |
60 |
0,86 |
0,71 |
170 |
0,26 |
0,11 |
70 |
0,81 |
0,60 |
180 |
0,23 |
0,10 |
80 |
0,75 |
0,48 |
190 |
0,21 |
0,09 |
90 |
0,69 |
0,38 |
200 |
0,19 |
0,08 |
100 |
0,60 |
0,31 |
210 |
0,17 |
0,07 |
6. Коефіцієнт запасу стійкості стержня дорівнює
.