
- •Базовая графика
- •Двухмерная графика
- •Векторная графика
- •Растровая графика
- •Фрактальная графика
- •Трёхмерная графика
- •Представление цветов в компьютере
- •Реальная сторона графики
- •Основные области применения
- •Современные стандарты компьютерной графики.
- •Графические диалоговые системы
- •Применение интерактивной графики в информационных системах
- •Знания и модели их представления: логическая, продукционная, реляционная, фреймы, семантические сети.
- •Язык программирования Пролог: структура программы, домены, предикаты, факты и правила, рекурсивные правила, динамические предикаты
- •Управляющие предикаты
- •Прочие стандартные предикаты
- •Факты в Прологе
- •Правила в Прологе
- •Методы организации рекурсии
- •Простая рекурсия
- •Метод обобщенного правила рекурсии (опр)
- •Реализация основных моделей представления знаний средствами языка Пролог
- •Общая проблема информационной безопасности информационных систем Безопасность информационных систем Основные понятия
- •Проблемы информационной безопасности
- •Защита информации при реализации информационных процессов. (ввод, вывод, передача, обработка, накопление, хранение)
- •Организационное обеспечение информационной безопасности
- •Защита информации от несанкционированного доступа
- •Глава 1. Защита от несанкционированного доступа к информации. Термины и определения
- •Глава 2. Основы правового регулирования отношений, связанных с конфиденциальной информацией
- •Глава 3. Правовая защита конфиденциальной информации и ответственность за неправомерные действия в отношении этой информации
- •Глава 4. Порядок учета, хранения и использования документов, содержащих конфиденциальную информацию
- •Математические и методические средства защиты
- •Средства защиты информации
Реализация основных моделей представления знаний средствами языка Пролог
Логическая модель знаний
Основная идея при построении логических моделей знаний заключается в следующем – вся информация, необходимая для решения прикладных задач, рассматривается как совокупность фактов и утверждений, которые представляются как формулы в некоторой логике. Знания отображаются совокупностью таких формул, а получение новых знаний сводится к реализации процедур логического вывода. В основе логических моделей знаний лежит понятие формальной теории, задаваемое картежем:
![]()
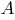 –
счетное
множество базовых символов (алфавит);
–
счетное
множество базовых символов (алфавит);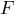 –
множество,
называемое формулами;
–
множество,
называемое формулами;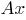 –
выделенное
подмножество априори истинных формул
(аксиом);
–
выделенное
подмножество априори истинных формул
(аксиом);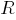 –
конечное
множество отношений между формулами,
называемое правилами вывода.
–
конечное
множество отношений между формулами,
называемое правилами вывода.
Основные достоинства логических моделей знаний:
в качестве «фундамента» здесь используется классический аппарат математической логики, методы которой достаточно хорошо изучены и формально обоснованы;
существуют достаточно эффективные процедуры вывода, в том числе реализованные в языке логического программирования «Пролог»;
в базах знаний можно хранить лишь множество аксиом, а все остальные знания получать из них по правилам вывода.
Продукционная модель знаний
Продукционные модели можно считать наиболее распространенными моделями представления знаний. Продукционная модель – это модель, основанная на правилах, позволяющая представить знание в виде предложений типа:
«ЕСЛИ условие, ТО действие»
Продукционная модель обладает тем недостатком, что при накоплении достаточно большого числа (порядка нескольких сотен) продукций они начинают противоречить друг другу.
В общем случае продукционную модель можно представить в следующем виде:
![]()
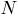 –
имя
продукции;
–
имя
продукции;– сфера применения продукции;
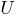 –
условие
применимости продукции;
–
условие
применимости продукции;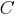 –
ядро
продукции;
–
ядро
продукции;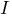 –
постусловия
продукции, актуализирующиеся при
положительной реализации продукции;
–
постусловия
продукции, актуализирующиеся при
положительной реализации продукции;– комментарий, неформальное пояснение (обоснование) продукции, время введения в базу знаний и т. д.;
Системы обработки знаний, использующие продукционную модель получили название «продукционных систем». В состав экспертных систем продукционного типа входят база правил (знаний), рабочая память и интерпретатор правил (решатель), реализующий определенный механизм логического вывода. Любое продукционное правило, содержащееся в базе знаний, состоит из двух частей: антецендента и консеквента. Антецедент представляет собой посылку правила (условную часть) и состоит из элементарных предложений, соединенных логическими связками «и», «или». Консеквент (заключение) включает одно или несколько предложений, которые выражают либо некоторый факт, либо указание на определенное действие, подлежащее исполнению. Продукционные правила принято записывать в виде антецедент-консеквент.
Семантические сети или сетевые модели знаний
Однозначное определение семантической сети в настоящее время отсутствует. В инженерии знаний под ней подразумевается граф, отображающий смысл целостного образа. Узлы графа соответствуют понятиям и объектам, а дуги – отношениям между объектами. Формально сеть можно задать в следующем виде:
![]()
– множество информационных единиц;
– множество типов связей между информационными единицами;
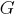 –
отображение,
задающее конкретные отношения из
имеющихся типов
между
элементами
.
–
отображение,
задающее конкретные отношения из
имеющихся типов
между
элементами
.
Семантическая
сеть как модель наиболее часто используется
для представления декларативных знаний.
С помощью этой модели реализуются такие
свойства системы знаний, как
интерпретируемость и связность, в том
числе по отношениям
![]() и
и
![]() .
За счет этих свойств семантическая сеть
позволяет снизить объем хранимых данных,
обеспечивает вывод умозаключений по
ассоциативным связям.
.
За счет этих свойств семантическая сеть
позволяет снизить объем хранимых данных,
обеспечивает вывод умозаключений по
ассоциативным связям.
Одной из первых известных моделей, основанных на семантической сети, является TLC-модель (Teachaple Languge Compre-hender – доступный механизм понимания языка), разработанная Куиллианом в 1968 году. Модель использовалась для представления семантических отношений между концептами (словами) с целью описания структуры долговременной памяти человека в психологии.
Как правило, различают экстенсиональные и интенсиональные семантические сети. Экстенсиональная семантическая сеть описывает конкретные отношения данной ситуации. Интенсиональная – имена классов объектов, а не индивидуальные имена объектов. Связи в интенсиональной сети отражают те отношения, которые всегда присущи объектам данного класса.
Фреймовая модель знаний
Фреймовая модель основана на концепции Марвина Мински (Marvin Minsky) – профессора Массачусетского технологического института, основателя лаборатории искусственного интеллекта, автора ряда фундаментальных работ. Фреймовая модель представляет собой систематизированную психологическую модель памяти человека и его сознания.
Фрейм (англ. frame – рамка, каркас) – структура данных для представления некоторого концептуального объекта. Информация, относящаяся к фрейму, содержится в составляющих его слотах.
Слот (англ. slot – щель, прорезь) может быть терминальным (листом иерархии) или представлять собой фрейм нижнего уровня.
Каждый фрейм, состоит из произвольного числа слотов, причем несколько из них обычно определяются самой системой для выполнения специфических функций, а остальные определяются пользователем.
Пояснение:
имя фрейма (имя фрейма) – это идентификатор, присваиваемый фрейму. Фрейм должен иметь имя, единственное в данной фреймовой модели (уникальное имя);
имя слота (имя слота) – это идентификатор, присваиваемый слоту. Слот должен иметь уникальное имя во фрейме, к которому он принадлежит. Обычно имя слота не несет никакой смысловой нагрузки и является лишь идентификатором данного слота, но в некоторых случаях оно может иметь специфический смысл;
указатель наследования – только для фреймовых моделей иерархического типа; они показывают, какую информацию об атрибутах слотов во фрейме верхнего уровня наследуют слоты с такими же именами во фрейме нижнего уровня;
указатель атрибутов – указатель типа данных слота. К таким типам относятся:
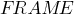 (указатель),
(указатель),
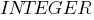 (целое),
(целое),
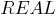 (вещественное),
(вещественное),
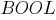 (булево),
(булево),
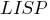 (присоединенная
процедура),
(присоединенная
процедура),
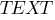 (текст),
(текст),
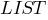 (список),
(список),
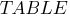 (таблица),
(таблица),
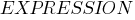 (выражение)
и другие;
(выражение)
и другие;значение слота – значение, соответствующее типу данных слота и удовлетворяющее условиям наследования;
демон – процедура, автоматически запускаемая при выполнении некоторого условия. Демоны запускаются при обращении к конкретному слоту фреймовой модели. Например, демон
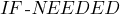 запускается,
если в момент обращения к слоту его
значение не было установлено,
запускается,
если в момент обращения к слоту его
значение не было установлено,
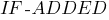 запускается
при подстановке в слот значения,
запускается
при подстановке в слот значения,
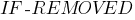 запускается
при стирании значения слота.
запускается
при стирании значения слота.
Фреймы образуют иерархию. Иерархия во фреймовых моделях порождает единую многоуровневую структуру, описывающую либо объект, если слоты описывают только свойства объекта, либо ситуацию или процесс, если отдельные слоты являются именами процедур, присоединенных к фрейму и вызываемых при его актуализации.
Формально фрейм – это тип данных вида:
![]()
– имя объекта;
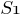 –
множество
слотов, содержащих факты, определяющие
декларативную семантику фрейма;
–
множество
слотов, содержащих факты, определяющие
декларативную семантику фрейма;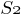 –
множество
слотов, обеспечивающих связи с другими
фреймами (каузальные, семантические и
т. д.);
–
множество
слотов, обеспечивающих связи с другими
фреймами (каузальные, семантические и
т. д.);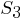 –
множество
слотов, обеспечивающих преобразования,
определяющие процедурную семантику
фрейма.
–
множество
слотов, обеспечивающих преобразования,
определяющие процедурную семантику
фрейма.
Фреймы подразделяются на:
фрейм-экземпляр – конкретная реализация фрейма, описывающая текущее состояние в предметной области;
фрейм-образец – шаблон для описания объектов или допустимых ситуаций предметной области;
фрейм-класс – фрейм верхнего уровня для представления совокупности фреймов образцов.
Состав фреймов и слотов в каждой конкретной фреймовой модели может быть разный, однако в рамках одной системы целесообразно единое представление для устранения лишнего усложнения.
Разнотипные объекты или объекты, соответствующие концепции «множественности миров», заключающейся, к примеру, в том, что лошадь – животное бескрылое для одного (реального) мира и одновременно крылатое (Пегас в мифическом мире) для другого, могут описываться отличающимися друг от друга фреймами.
В целом фреймовая модель допускает представление всех свойств декларативных и процедурных знаний. Глубина вложенности слотов во фрейме (число уровней) зависит от предметной области и языка, реализующего модель.
Вывод в продукционных моделях. Механизм логического вывода и рекурсия
Процедура логического вывода в системах, основанных на продукционных моделях, в принципе не сложная. Как правило, она включает следующие части:
рабочую память (базу данных) – фактические данные, описывающие возможное и текущее состояние предметной области – хранящуюся в оперативной памяти;
базу продукционных правил, содержащую все допустимые зависимости между фактами предметной области и хранящуюся в долговременной памяти;
механизм логического вывода.
Механизм логического вывода обеспечивает формирование заключений, воспринимая вводимые факты как элементы правил, отыскивая правила, в состав которых входят введенные факты, и актуализируя те части продукций, которым соответствуют введенные факты. Теоретической основой построения механизма логического вывода служит теория машины Поста.
Механизм логического вывода выполняет функции поиска в базе правил, последовательного выполнения операций над знаниями и получения заключений. Существует два способа проведения таких заключений – прямые выводы и обратные выводы.
Пусть имеется совокупность продукций в виде цепочек правил:
![]()
![]()
Прямым выводам (прямой цепочке рассуждений) соответствует движение от посылок к следствиям.
Механизм
логического вывода, использующий прямые
выводы, в качестве образца выбирает
введенный в базу данных (рабочую память)
факт
и
если при сопоставлении он согласуется
с посылкой правила, то делается заключение
![]() ,
которое тоже помещается в базу данных
как факт, описывающий состояние предметной
области. Последовательно выводятся
новые результаты, начиная с уже известных.
Однако отсутствие связи между фактами
и
может
привести к обрыву процедуры и конечный
результат
,
которое тоже помещается в базу данных
как факт, описывающий состояние предметной
области. Последовательно выводятся
новые результаты, начиная с уже известных.
Однако отсутствие связи между фактами
и
может
привести к обрыву процедуры и конечный
результат
![]() не
может быть получен. Это считается
основным недостатком прямых механизмов
логического вывода и требует от
пользователя знания всей структуры
модели предметной области. Особенно
явно этот недостаток проявляется при
включении в базу знаний новых фактов и
правил: если они не связаны в цепочку с
имеющимися фактами, то они становятся
балластом – механизм логического вывода
никогда их не найдет. С этой точки зрения
использование обратной цепочки
рассуждений предпочтительнее.
не
может быть получен. Это считается
основным недостатком прямых механизмов
логического вывода и требует от
пользователя знания всей структуры
модели предметной области. Особенно
явно этот недостаток проявляется при
включении в базу знаний новых фактов и
правил: если они не связаны в цепочку с
имеющимися фактами, то они становятся
балластом – механизм логического вывода
никогда их не найдет. С этой точки зрения
использование обратной цепочки
рассуждений предпочтительнее.
Обратным выводам (обратной цепочке рассуждений) соответствует движение от цели (факта, который требуется установить) к предпосылкам. В обратном механизме логического вывода работа начинается от поставленной цели. Если цель согласуется с консеквентом (заключением) продукции, то антецедент (посылка) принимается за подцель и делается попытка подтверждения истинности этого факта. Процесс повторяется до тех пор, пока не будут просмотрены все правила, имеющие в качестве заключения требуемый факт.
Так,
в приведенном примере движение от
заключения
приводит
к необходимости подтверждения факта
![]() .
Факт
может
подтвердиться, если подтверждается
.
Если
не
подтверждается, то механизм логического
вывода отыщет правило, связывающее
с
.
Факт
может
подтвердиться, если подтверждается
.
Если
не
подтверждается, то механизм логического
вывода отыщет правило, связывающее
с
![]() и
перейдет на анализ второй цепочки
правил. Дойдя до правила
и
перейдет на анализ второй цепочки
правил. Дойдя до правила
![]() ,
система запросит базу данных (рабочую
память) или пользователя о справедливости
факта
.
Если факт
подтверждается,
то происходит возвратное движение по
правилам, все факты актуализируются
(считаются справедливыми) и цель
достигается успешно. В противном случае
система явно указывает причину
недоказанности выводов, что, в отличие
от прямой цепочки рассуждений, облегчает
работу пользователя.
,
система запросит базу данных (рабочую
память) или пользователя о справедливости
факта
.
Если факт
подтверждается,
то происходит возвратное движение по
правилам, все факты актуализируются
(считаются справедливыми) и цель
достигается успешно. В противном случае
система явно указывает причину
недоказанности выводов, что, в отличие
от прямой цепочки рассуждений, облегчает
работу пользователя.
Функцией, реализующей работу механизма логического вывода, является рекурсивная процедура сопоставления с образцом.
Рекурсия (лат. «recurso» – бегу назад, спешу обратно, возвращаюсь) – способ решения задач, заключающийся в разбиении исходной задачи на подзадачи. Если подзадача есть уменьшенный вариант исходной задачи, то способ ее разбиения и решения идентичен примененному к исходной задаче. Последовательное разбиение приводит к задаче, решаемой непосредственно. Это решение служит основанием для решения подзадачи верхнего уровня и т. д., пока первоначальная задача не будет решена.
Информационная безопасность и защита информации
